高压放大器是一种特殊类型的放大器,主要用于将低电压信号放大到高电压水平。它在许多领域中具有重要的应用,如医学成像、科学研究、工业设备等。为了正确选择和评估高压放大器,我们需要了解其主要技术指标。以下是高压放大器的主要技术指标的详细介绍:
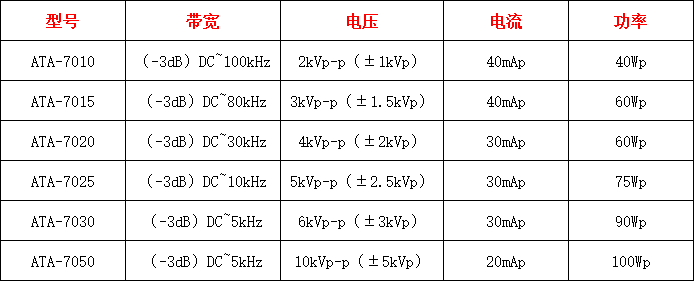
图:ATA-7000系列高压放大器
最大输出电压:最大输出电压是高压放大器可以提供的最高电压数值。它代表了放大器的能力,通常以伏特(V)为单位。最大输出电压取决于放大器的设计和电源电压的限制。选择高压放大器时,需要确保其最大输出电压能够满足所需应用的要求。
频率响应:频率响应指的是高压放大器在不同频率范围内能够提供稳定放大的能力。它表征了放大器在不同频率信号上的增益特性。对于需要放大宽带信号或高频信号的应用,需要选择具有宽频率响应范围的高压放大器。
增益:增益是指高压放大器输出信号与输入信号之间的比例关系。它表示了放大器可以将输入信号放大的倍数。增益通常用分贝(dB)作为单位,常见的高压放大器的增益范围从几十倍到几百倍不等。选择合适的增益取决于输入信号的幅度和所需输出电压的目标。
噪音:噪音是高压放大器输出信号中的随机波动。高压放大器应尽可能降低噪音水平,以提供清晰的输出信号。噪音常以噪声系数来描述,更低的噪声系数表示更低的噪音水平。

图:ATA-7010高压放大器指标参数
带宽:带宽是高压放大器能够放大信号的频率范围。它表示了放大器可以保持稳定增益的频率范围。选择适当的带宽取决于应用中的信号频率要求。
稳定性:稳定性是指高压放大器的输出特性在不同温度、电源波动等环境变化下的稳定程度。放大器应具有良好的稳定性,以确保输出信号的准确性和可靠性。
高压放大器的主要技术指标包括最大输出电压、频率响应、增益、噪音、带宽和稳定性。根据具体的应用需求,选择合适的高压放大器并评估其技术指标是确保系统性能和信号质量的关键。