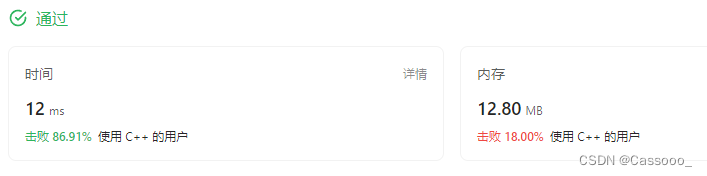
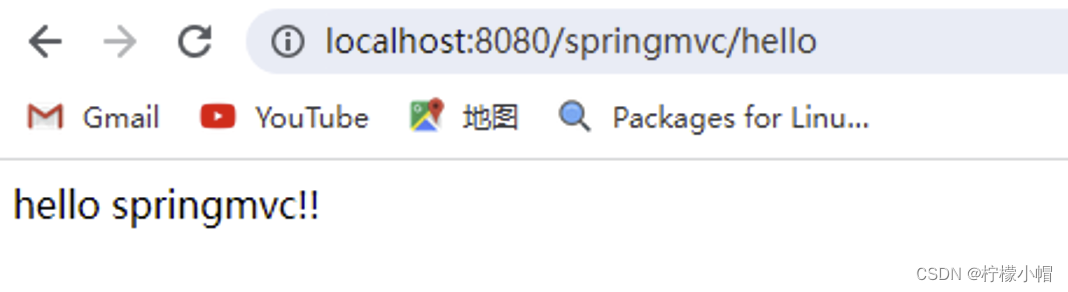
题目描述:

解题思路:双指针
四数之和与前面三数之和思路一样,排序后,枚举 nums[a]作为第一个数,枚举 nums[b]作为第二个数,那么问题变成找到另外两个数,使得这四个数的和等于 target,也是用双指针解决。
对于 nums[a]的枚举:
- 设 s=nums[a]+nums[a+1]+nums[a+2]+nums[a+3]。如果 s>targets,由于数组已经排序,后面无论怎么选,选出的四个数的和不会比 s 还小,所以后面不会找到等于 target的四数之和了。所以只要 s>targets,就可以直接 break 外层循环了。
- 设 s=nums[a]+nums[n−3]+nums[n−2]+nums[n−1]。如果 s<targets,由于数组已经排序,nums[a]加上后面任意三个数都不会超过 s,所以无法在后面找到另外三个数与 nums[a]相加等于 target。但是后面还有更大的 nums[a],可能出现四数之和等于 target的情况,所以还需要继续枚举,continue 外层循环。
- 如果 a>0且 nums[a]=nums[a−1],那么 nums[a]和后面数字相加的结果,必然在之前算出过,所以无需执行后续代码,直接 continue 外层循环。(可以放在循环开头判断。)
对于 nums[b]的枚举(b从 a+1开始),也同样有类似优化:
- 设 s=nums[a]+nums[b]+nums[b+1]+nums[b+2]。如果 s>targets,由于数组已经排序,后面无论怎么选,选出的四个数的和不会比 s还小,所以后面不会找到等于 target的四数之和了。所以只要 s>targets,就可以直接 break。
- 设 s=nums[a]+nums[b]+nums[n−2]+nums[n−1]。如果 s<targets,由于数组已经排序,nums[a]+nums[b]加上后面任意两个数都不会超过 sss,所以无法在后面找到另外两个数与 nums[a]和 nums[b]相加等于 target\。但是后面还有更大的 nums[b],可能出现四数之和等于 target的情况,所以还需要继续枚举,continue。
- 如果 b>a+1且 nums[b]=nums[b−1],那么 nums[b]和后面数字相加的结果,必然在之前算出过,所以无需执行后续代码,直接 continue。注意这里 b>a+1的判断是必须的,如果不判断,对于示例 2 这样的数据,会直接 continue,漏掉符合要求的答案。
另外:对于C++语言,相加结果可能会超过32位整数范围,需要用64位整数存储四数之和。
代码:
class Solution
{
public:
vector<vector<int>> fourSum(vector<int> &nums, int target)
{
sort(nums.begin(), nums.end());
vector<vector<int>> ans;
int n = nums.size();
for (int a = 0; a < n - 3; a++) // 枚举第一个数
{
long long x = nums[a]; // 使用 long long 避免溢出
if (a > 0 && x == nums[a - 1])
continue; // 跳过重复数字
if (x + nums[a + 1] + nums[a + 2] + nums[a + 3] > target)
break; // 优化一
if (x + nums[n - 3] + nums[n - 2] + nums[n - 1] < target)
continue; // 优化二
for (int b = a + 1; b < n - 2; b++) // 枚举第二个数
{
long long y = nums[b];
if (b > a + 1 && y == nums[b - 1])
continue; // 跳过重复数字
if (x + y + nums[b + 1] + nums[b + 2] > target)
break; // 优化一
if (x + y + nums[n - 2] + nums[n - 1] < target)
continue; // 优化二
int c = b + 1, d = n - 1;
while (c < d) // 双指针枚举第三个数和第四个数
{
long long s = x + y + nums[c] + nums[d]; // 四数之和
if (s > target)
d--;
else if (s < target)
c++;
else // s == target
{
ans.push_back({(int) x, (int) y, nums[c], nums[d]});
for (c++; c < d && nums[c] == nums[c - 1]; c++); // 跳过重复数字
for (d--; d > c && nums[d] == nums[d + 1]; d--); // 跳过重复数字
}
}
}
}
return ans;
}
};结果: