第一步:记住公式,绝对值差,和差绝对值,绝对值和
第二步:记住口诀:取等条件:中间相加取等号,左异右同零取到;中间相减取等号,上面符号方向调
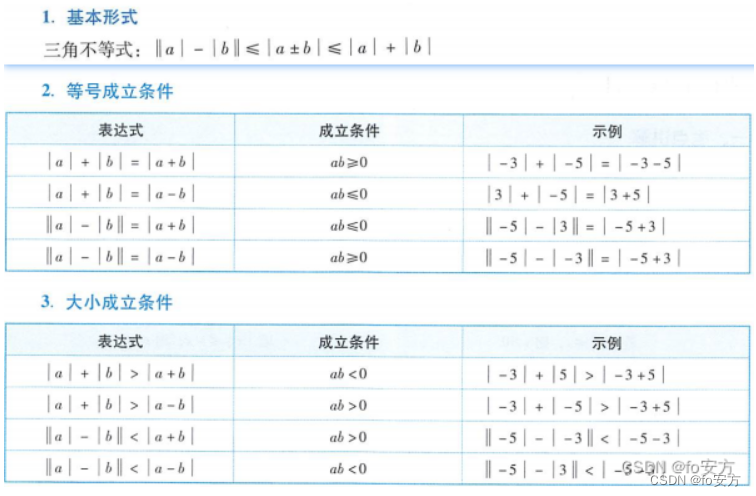
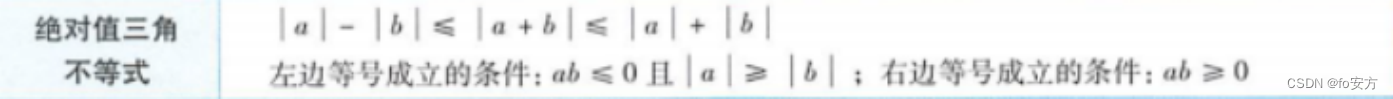


题型记忆法

歌诀记忆法
左异右同,可以为零
左同右异,可以为零


取等条件:中间相加取等号,左异右同零取到;中间相减取等号,上面符号方向调


向量记忆法
绝对值三角不等式取等号技巧
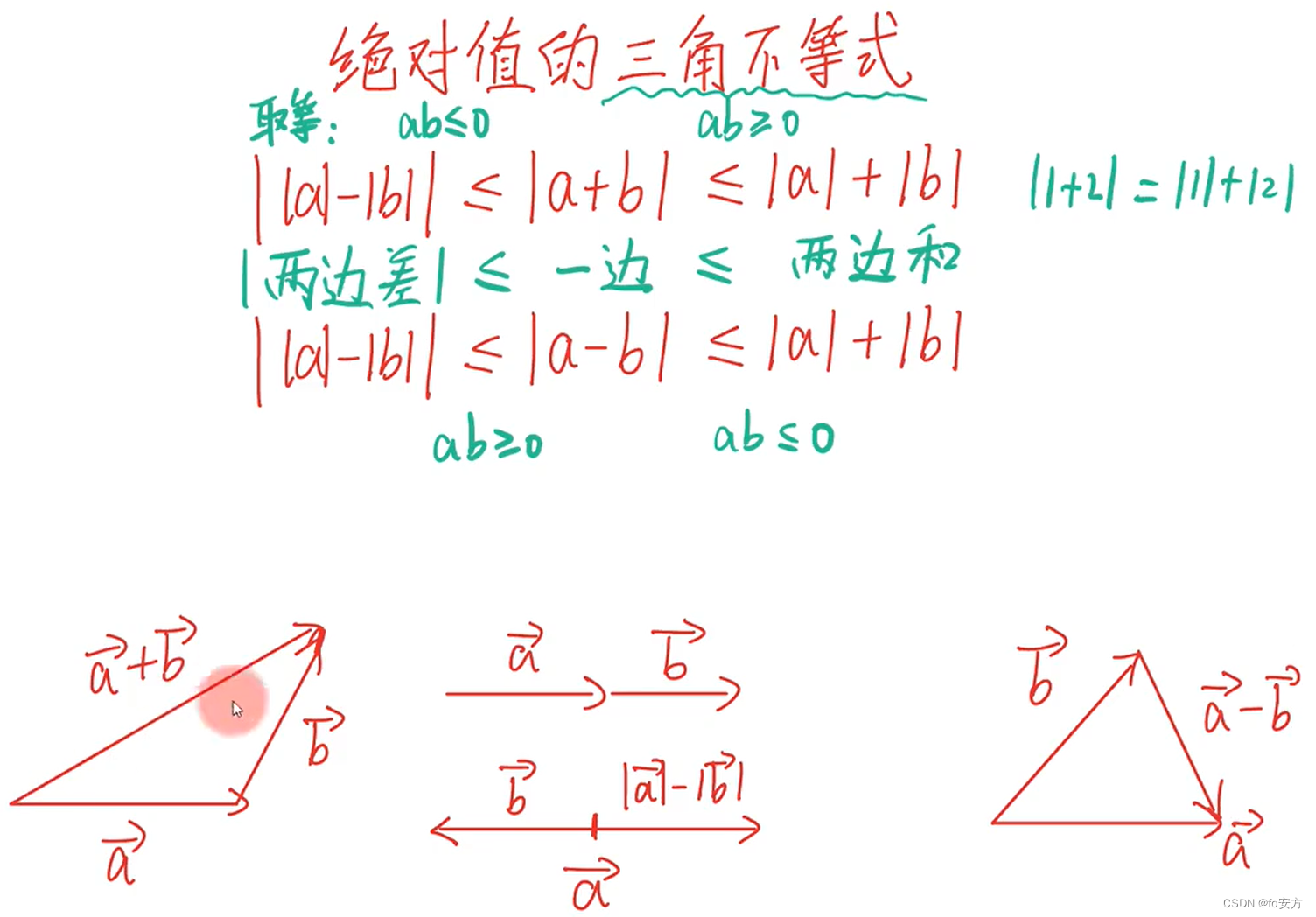
向量构成三角形,三角形中有两边之和大于第三边,即|a|+|b|≥|a+b|,当向量方向相同时,可以取等于。同理,三角形中有两边之差小于第三边,即|a+b|≥||a|-|b||。
or
结合三角形的性质,
两边之和大于第三边,两边之差小于第三边。
将a、b、a+b看成组成三角三条边的向量,边的长度为向量的膜。
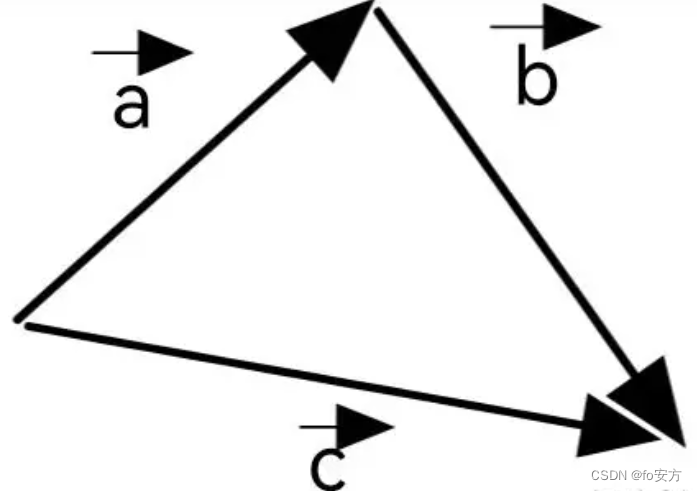
等于的情况就不能用三角形?等于就是两条边压平到一定程度,和第三条边重合了
理解记忆法
∵||a|-|b||、|a±b|、|a|+|b|均为非负数
∴分别比较其平方的大小
平方分别为:
(
∣
∣
a
∣
−
∣
b
∣
∣
)
2
=
a
2
−
2
∣
a
∣
∣
b
∣
+
b
2
(||a|-|b||)^2=a^2-2|a||b|+b^2
(∣∣a∣−∣b∣∣)2=a2−2∣a∣∣b∣+b2
(
∣
a
±
b
∣
)
2
=
(
a
±
b
)
2
=
a
2
±
2
a
b
+
b
2
(|a±b|)^2=(a±b)^2=a^2±2ab+b^2
(∣a±b∣)2=(a±b)2=a2±2ab+b2
(
∣
a
∣
+
∣
b
∣
)
2
=
a
2
+
2
∣
a
∣
∣
b
∣
+
b
2
(|a|+|b|)^2=a^2+2|a||b|+b^2
(∣a∣+∣b∣)2=a2+2∣a∣∣b∣+b2
其中
(
−
2
∣
a
∣
∣
b
∣
)
≤
(
±
2
a
b
)
≤
2
∣
a
∣
∣
b
∣
(-2|a||b|) ≤(±2ab)≤ 2|a||b|
(−2∣a∣∣b∣)≤(±2ab)≤2∣a∣∣b∣
证毕。
考题记忆法
https://zhuanlan.zhihu.com/p/38328863





![【leetcode】 vscode leetcode [ERROR] invalid password? 问题解决](https://img-blog.csdnimg.cn/338ca18449ad4f57831a1283923d2bf6.png)