题目

110. 平衡二叉树

简单

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

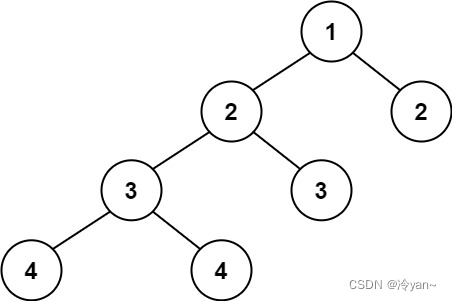
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

• 树中的节点数在范围 [0, 5000] 内
• -104 <= Node.val <= 104

思路和解题方法

        首先，我们需要了解平衡二叉树的定义：对于任意一个节点，其左子树和右子树的高度差不超过1。

        在这段代码中，我们定义了一个递归函数getHeight，用于计算以某个节点为根节点的二叉树的高度并判断是否为平衡二叉树。其中，如果节点为空，则返回0表示该节点为叶节点；否则，分别递归计算它的左子树和右子树的高度。如果左子树或右子树不为平衡二叉树，则直接返回-1表示以该节点为根节点的二叉树不是平衡二叉树。如果左右子树的高度差超过1，则也返回-1。最后，如果满足平衡二叉树定义，则返回以该节点为根节点的二叉树的高度，即左右子树中较大的高度加上1。

        在主函数isBalanced中，我们调用getHeight函数来计算整棵二叉树的高度。如果返回值为-1，则整棵树不是平衡二叉树，返回false；否则整棵树为平衡二叉树，返回true。

复杂度

        时间复杂度:

               O(nlogn)

        空间复杂度

                O(n)

c++ 代码

 ​

class Solution {
public:
    // 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1
    int getHeight(TreeNode* node) {
        if (node == NULL) {  // 如果节点为空，则返回0，表示该节点为叶节点
            return 0;
        }
        int leftHeight = getHeight(node->left);  // 递归计算左子树的高度
        if (leftHeight == -1) return -1;  // 左子树不是平衡二叉树，则直接返回-1
        int rightHeight = getHeight(node->right);  // 递归计算右子树的高度
        if (rightHeight == -1) return -1;  // 右子树不是平衡二叉树，则直接返回-1
        return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);  // 如果满足平衡二叉树的定义，则返回以该节点为根节点的二叉树的高度
    }

    bool isBalanced(TreeNode* root) {
        return getHeight(root) == -1 ? false : true;  // 如果返回-1，则整棵树不是平衡二叉树，否则整棵树是平衡二叉树
    }
};

觉得有用的话可以点点赞，支持一下。

如果愿意的话关注一下。会对你有更多的帮助。

每天都会不定时更新哦  >人<  。