1.1 动态规划简介
1.1.1 引例
动态规划算法和分治法类似,基本思想也是将待求解问题分解成若干个子问题,子问题可以以继续拆分,直到问题规模达到临界条件即可。多说无益,举个例子来解释一下:
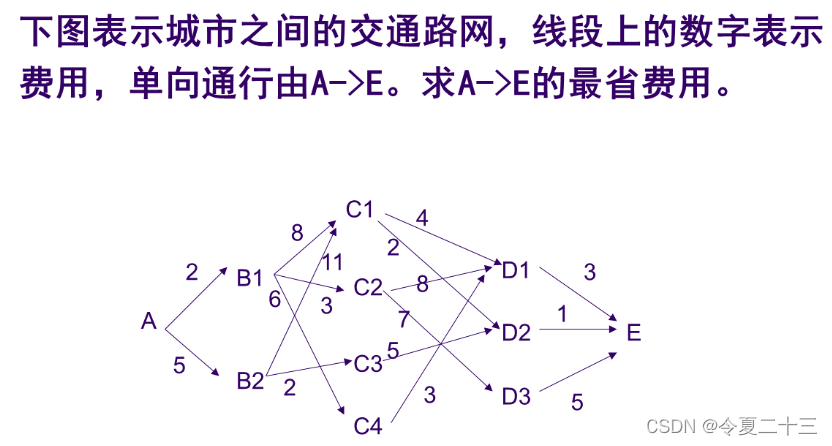
这其实是一个多阶段图求最短路的问题,路径大体上是 A→B→C→D→E,但是每到一个节点时就需要面临许多选择,所有选择中加起来最短的那一组就是要求的答案。
我们可以用动态规划的思想来分析这个问题,最开始从A出发,我们要选择一条最短的路,那么就可以把这个大问题先分成两个:从A到B和从B到E,这样就把大问题拆成两个小问题了,接下来,从A到B有两个选择,分别是B1和B2,它们和从B到E的路径相连,接下来就可以继续拆分,从B1到E和从B2到E又可以拆分成两个小问题,那就是从B到C和从C到E.......就这样一直拆下去,直到最后从D到E,这样再往回返回最短路径,直到得到整个问题的最短路径。
1.1.2 算法总体思想
从上面我们知道,动态规划算法也是不断地拆分问题,但是这里和之前的递归又有所不同,因为动态规划类的问题中,分解得到的子问题一般不会是相互独立的,也就是说有可能得到相同的子问题,所以在计算中,如果单单应用了递归,有些子问题就会被重复计算。
因此,适合使用动态规划来解决的问题一般都有下面两个性质:
1. 最优子结构性质
一个问题的最优解包含了其子问题的最优解。
2. 重叠子问题性质
在问题的求解过程中,很多子问题的解会被多次使用。