文章前言：如果不知道什么是前序与中序的小白同学，作者推荐：二叉树的初步认识_加瓦不加班的博客-CSDN博客

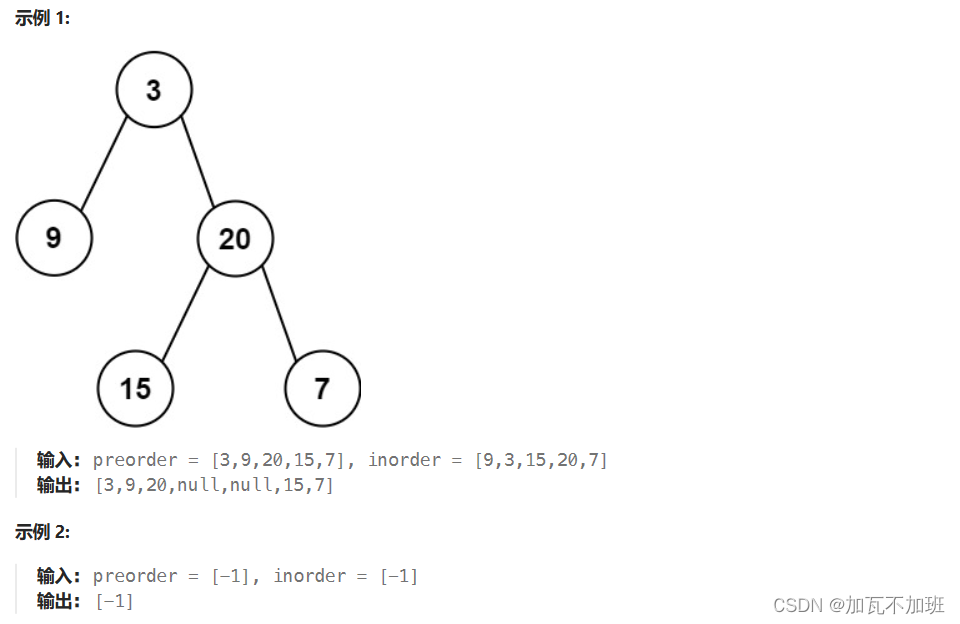
思路：

• 先通过前序遍历结果定位根节点

• 再结合中序遍历结果切分左右子树

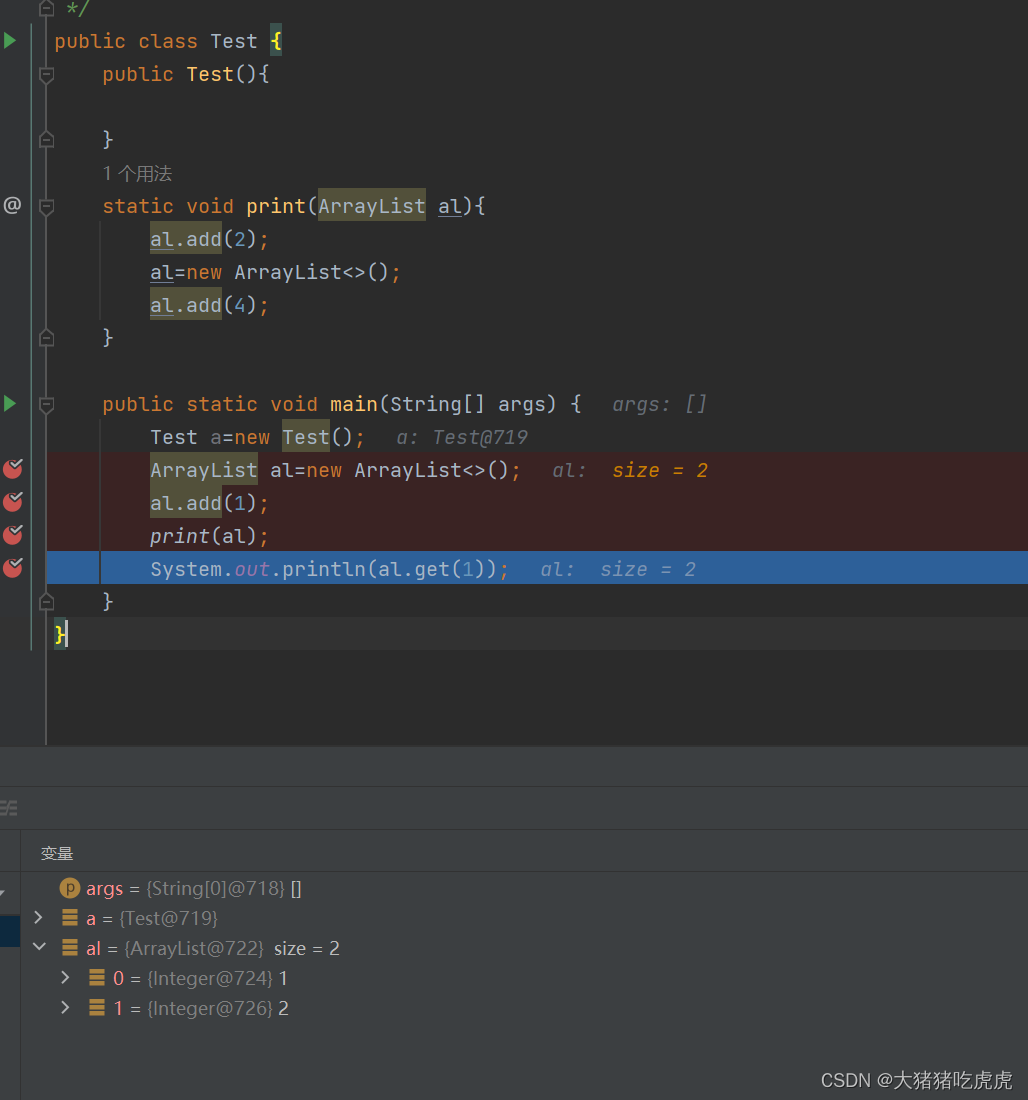
public class E09Leetcode105 {
    //1. pre-order 前序遍历，对于每一棵子树，先访问该节点，然后是左子树，最后是右子树
	//2. in-order 中序遍历，对于每一棵子树，先访问左子树，然后是该节点，最后是右子树
	//3. post-order 后序遍历，对于每一棵子树，先访问左子树，然后是右子树，最后是该节点
    /*
        preOrder = {1,2,4,3,6,7}
        inOrder = {4,2,1,6,3,7}

       1.根据前序可以得知： 根是 1
       2.根据中序可以得知： 我们已经知道根节点是1 那么就能判断中序中1之前的是左子树  1后面的是右子树
       
            pre         in
        左  2,4         4,2
        右  3,6,7       6,3,7

		3.然后我们再根据前序的性质就知道顺序
        根 2
        左 4

        根 3
        左 6
        右 7
     */

    //preOrder:传入的是前序遍历的数组  inOrder:传入的是中序遍历的数组
    public TreeNode buildTree(int[] preOrder, int[] inOrder) {
        if (preOrder.length == 0) {
            return null;
        }
        // 创建根节点
        int rootValue = preOrder[0];
        TreeNode root = new TreeNode(rootValue);
        // 利用中序遍历的数组区分左右子树
        for (int i = 0; i < inOrder.length; i++) {
            //在中序遍历的数组中找到根节点
            if (inOrder[i] == rootValue) {
                // 0 ~ i-1 左子树
                // i+1 ~ inOrder.length -1 右子树
                int[] inLeft = Arrays.copyOfRange(inOrder, 0, i); // [4,2]
                int[] inRight = Arrays.copyOfRange(inOrder, i + 1, inOrder.length); // [6,3,7]

                int[] preLeft = Arrays.copyOfRange(preOrder, 1, i + 1); // [2,4]
                int[] preRight = Arrays.copyOfRange(preOrder, i + 1, inOrder.length); // [3,6,7]

                root.left = buildTree(preLeft, inLeft); // 2
                root.right = buildTree(preRight, inRight); // 3
                break;
            }
        }
        return root;
    }

}

• 代码可以进一步优化，涉及新数据结构，以后实现