第八课 二分

lc704.二分查找–简单

题目描述

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

代码展示

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while(left <= right){
            int mid = (right - left) / 2 + left;
            int num = nums[mid];
            if (num == target) {
                return mid;
            } else if (num > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }
};

二分模版

lc34.排序数组中查找元素的第一个和最后一个位置–中等

题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

• 0 <= nums.length <= 105
• -109 <= nums[i] <= 109
• nums 是一个非递减数组
• -109 <= target <= 109

代码展示

class Solution {
     
  // 两次二分查找，分开查找第一个和最后一个
  // 时间复杂度 O(log n), 空间复杂度 O(1)
  // [1,2,3,3,3,3,4,5,9]
  public int[] searchRange(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    int first = -1;
    int last = -1;
    // 找第一个等于target的位置
    while (left <= right) {
      int middle = (left + right) / 2;
      if (nums[middle] == target) {
        first = middle;
        right = middle - 1; //重点
      } else if (nums[middle] > target) {
        right = middle - 1;
      } else {
        left = middle + 1;
      }
    }

    // 最后一个等于target的位置
    left = 0;
    right = nums.length - 1;
    while (left <= right) {
      int middle = (left + right) / 2;
      if (nums[middle] == target) {
        last = middle;
        left = middle + 1; //重点
      } else if (nums[middle] > target) {
        right = middle - 1;
      } else {
        left = middle + 1;
      }
    }

    return new int[]{first, last};
  }
}

lc69.x的平方根–简单

题目描述

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

**注意：**不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

• 0 <= x <= 231 - 1

代码展示

class Solution {
public:
    int mySqrt(int x) {
        // 找最大的ans，满足ans^2<=x
        long long left = 0, right = x;
        while (left < right) {
            long long mid = (left + right + 1) / 2;
            if (mid * mid <= x) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return right;
    }
};

lc74.搜索二维矩阵–中等

题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非递减顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

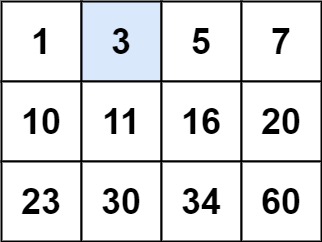
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

代码展示

class Solution {
public:       //两次二分查找
    bool searchMatrix(vector<vector<int>> matrix, int target) {
        auto row = upper_bound(matrix.begin(), matrix.end(), target, [](const int b, const vector<int> &a) {
            return b < a[0];
        });
        if (row == matrix.begin()) {
            return false;
        }
        --row;
        return binary_search(row->begin(), row->end(), target);
    }
};

class Solution {
public:       //一次二分查找
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int low = 0, high = m * n - 1;
        while (low <= high) {
            int mid = (high - low) / 2 + low;
            int x = matrix[mid / n][mid % n];
            if (x < target) {
                low = mid + 1;
            } else if (x > target) {
                high = mid - 1;
            } else {
                return true;
            }
        }
        return false;
    }
};

lc153.寻找旋转排序数组中的最小值–中等

题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 中的所有整数 互不相同
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

代码展示

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0;
        int right = nums.size() - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            // 如果中间元素大于右边元素，说明最小值在右半部分
            if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else {
                // 否则最小值在左半部分或者就是中间元素
                right = mid;
            }
        }

        // 最小元素就是左边界元素
        return nums[left];
    }
};

lc154.寻找寻找排序数组中的最小值II–困难

题目描述

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
• 若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须尽可能减少整个过程的操作步骤。

示例 1：

输入：nums = [1,3,5]
输出：1

示例 2：

输入：nums = [2,2,2,0,1]
输出：0

提示：

• n == nums.length
• 1 <= n <= 5000
• -5000 <= nums[i] <= 5000
• nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

代码展示

class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0;
        int right = nums.size() - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            // 如果中间元素大于右边元素，说明最小值在右半部分
            if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else if (nums[mid] < nums[right]) {
                // 如果中间元素小于右边元素，说明最小值在左半部分或者就是中间元素
                right = mid;
            } else {
                // 如果中间元素等于右边元素，无法确定最小值在左半部分还是右半部分
                // 只能将右边界向左移动一个位置，继续搜索
                right--;
            }
        }

        // 最小元素就是左边界元素
        return nums[left];
    }
};
//这段代码在二分查找的基础上，处理了可能存在重复元素值的情况。在中间元素等于右边元素时，将右边界
//向左移动一个位置，继续搜索，以确保找到最小元素。这样的算法复杂度仍然是 O(log n)。

三分查找

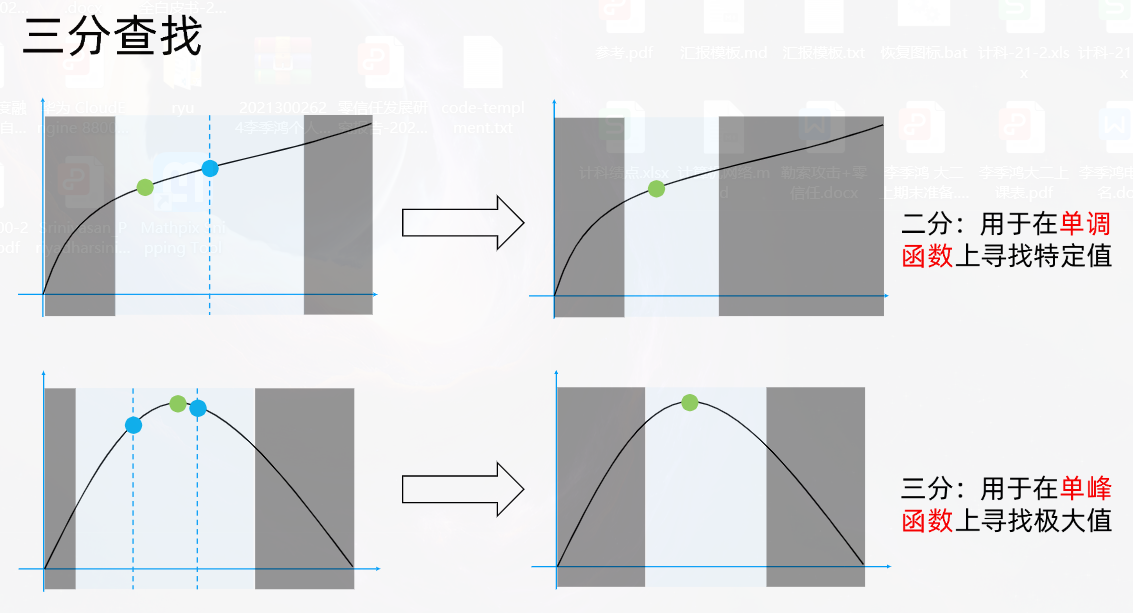
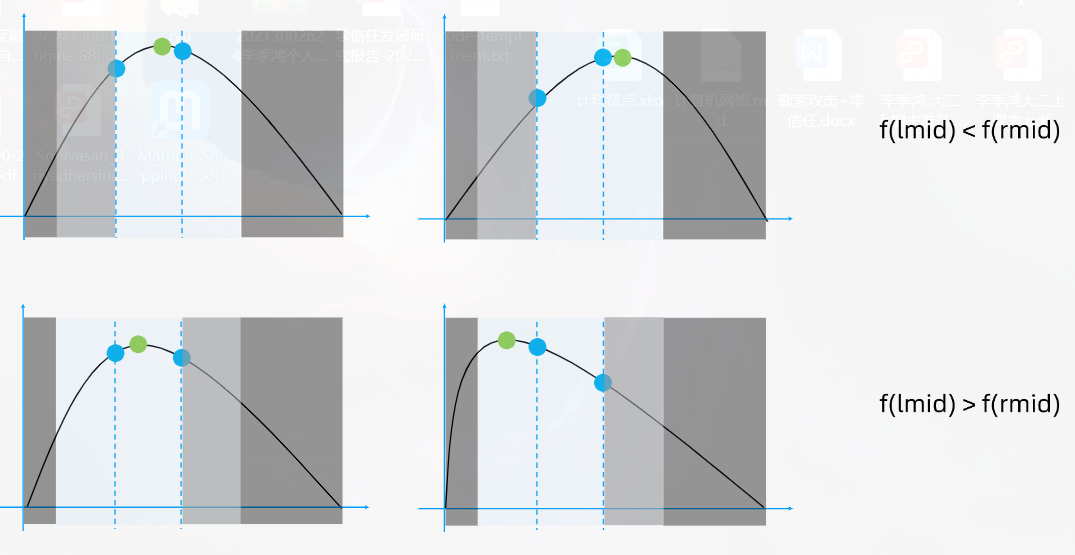
lc162.寻找峰值–中等

题目描述

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

示例 1：

输入：nums = [1,2,3,1]
输出：2
解释：3 是峰值元素，你的函数应该返回其索引 2。

示例 2：

输入：nums = [1,2,1,3,5,6,4]
输出：1 或 5 
解释：你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

提示：

• 1 <= nums.length <= 1000
• -231 <= nums[i] <= 231 - 1
• 对于所有有效的 i 都有 nums[i] != nums[i + 1]

代码展示

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int left = 0;
        int right = nums.size() - 1;

        while (left < right) {
            int mid = left + (right - left) / 2;

            // 如果中间元素小于其右边元素，说明峰值在右半部分
            if (nums[mid] < nums[mid + 1]) {
                left = mid + 1;
            } else {
                // 否则峰值在左半部分或者就是中间元素
                right = mid;
            }
        }

        // 返回左边界，即峰值所在位置
        return left;
    }
};
//这段代码使用二分查找，通过比较中间元素和其右边元素的大小来决定峰值在哪一侧，然后不断缩小搜索范
//围，直到找到峰值元素的索引。由于每次将搜索范围缩小一半，这个算法的时间复杂度为 O(log n)。

lc374.猜数字大小–简单

题目描述

猜数字游戏的规则如下：

• 每轮游戏，我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
• 如果你猜错了，我会告诉你，你猜测的数字比我选出的数字是大了还是小了。

你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果，返回值一共有 3 种可能的情况（-1，1 或 0）：

• -1：我选出的数字比你猜的数字小 pick < num
• 1：我选出的数字比你猜的数字大 pick > num
• 0：我选出的数字和你猜的数字一样。恭喜！你猜对了！pick == num

返回我选出的数字。

示例 1：

输入：n = 10, pick = 6
输出：6

示例 2：

输入：n = 1, pick = 1
输出：1

示例 3：

输入：n = 2, pick = 1
输出：1

示例 4：

输入：n = 2, pick = 2
输出：2

提示：

• 1 <= n <= 231 - 1
• 1 <= pick <= n

代码展示

// Forward declaration of guess API.
int guess(int num);

class Solution {
public:
    int guessNumber(int n) {
        int left = 1;
        int right = n;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            int result = guess(mid);

            if (result == 0) {
                return mid; // 找到了答案
            } else if (result == 1) {
                left = mid + 1; // 答案在右半部分
            } else {
                right = mid - 1; // 答案在左半部分
            }
        }

        return -1; // 未找到答案，这里可以根据具体情况返回 -1 或其他合适的值
    }
};

二分答案–最优性问题转化为判定问题的基本技巧

lc410.分割数组的最大值–困难

题目描述

给定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

设计一个算法使得这 m 个子数组各自和的最大值最小。

示例 1：

输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。 
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

示例 2：

输入：nums = [1,2,3,4,5], m = 2
输出：9

示例 3：

输入：nums = [1,4,4], m = 3
输出：4

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 106
• 1 <= m <= min(50, nums.length)

代码展示

class Solution {
public:
    int splitArray(vector<int>& nums, int k) {
        long long left = 0;
        long long right = 0;
        
        // 计算 left 和 right 的边界
        for (int num : nums) {
            left = max(left, (long long)num);
            right += num;
        }
        
        while (left < right) {
            long long mid = left + (right - left) / 2;
            
            if (canSplit(nums, k, mid)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        
        return left;
    }
    
    bool canSplit(vector<int>& nums, int k, long long maxSum) {
        int count = 1;
        long long sum = 0;
        
        for (int num : nums) {
            sum += num;
            if (sum > maxSum) {
                count++;
                sum = num;
            }
        }
        
        return count <= k;
    }
};

本质:

二分答案的本质是建立一个单调分段0/1函数，定义域为解空间（答案），值域为0或1，
在这个函数上二分查找分界点

lc1482.制作m束花所需的最少天数–中等

题目描述

给你一个整数数组 bloomDay，以及两个整数 m 和 k 。

现需要制作 m 束花。制作花束时，需要使用花园中 相邻的 k 朵花 。

花园中有 n 朵花，第 i 朵花会在 bloomDay[i] 时盛开，恰好 可以用于 一束 花中。

请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。

示例 1：

输入：bloomDay = [1,10,3,10,2], m = 3, k = 1
输出：3
解释：让我们一起观察这三天的花开过程，x 表示花开，而 _ 表示花还未开。
现在需要制作 3 束花，每束只需要 1 朵。
1 天后：[x, _, _, _, _]   // 只能制作 1 束花
2 天后：[x, _, _, _, x]   // 只能制作 2 束花
3 天后：[x, _, x, _, x]   // 可以制作 3 束花，答案为 3

示例 2：

输入：bloomDay = [1,10,3,10,2], m = 3, k = 2
输出：-1
解释：要制作 3 束花，每束需要 2 朵花，也就是一共需要 6 朵花。而花园中只有 5 朵花，无法满足制作要求，返回 -1 。

示例 3：

输入：bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
输出：12
解释：要制作 2 束花，每束需要 3 朵。
花园在 7 天后和 12 天后的情况如下：
7 天后：[x, x, x, x, _, x, x]
可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花，因为它们不相邻。
12 天后：[x, x, x, x, x, x, x]
显然，我们可以用不同的方式制作两束花。

示例 4：

输入：bloomDay = [1000000000,1000000000], m = 1, k = 1
输出：1000000000
解释：需要等 1000000000 天才能采到花来制作花束

示例 5：

输入：bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2
输出：9

提示：

• bloomDay.length == n
• 1 <= n <= 10^5
• 1 <= bloomDay[i] <= 10^9
• 1 <= m <= 10^6
• 1 <= k <= n

代码展示

class Solution {
public:
    int minDays(vector<int>& bloomDay, int m, int k) {
        // 如果需要的花束数量大于花朵总数除以每束花的数量，无法制作足够的花束，返回 -1
        if (m > bloomDay.size() / k) {
            return -1;
        }
        
        // 初始化最小和最大等待天数
        int low = INT_MAX, high = 0;
        int length = bloomDay.size();
        for (int i = 0; i < length; i++) {
            low = min(low, bloomDay[i]); // 更新最小等待天数
            high = max(high, bloomDay[i]); // 更新最大等待天数
        }
        
        // 二分查找
        while (low < high) {
            int days = (high - low) / 2 + low; // 当前猜测的等待天数
            if (canMake(bloomDay, days, m, k)) {
                high = days; // 在当前天数内可以制作足够的花束，将 high 缩小到 days
            } else {
                low = days + 1; // 在当前天数内无法制作足够的花束，将 low 增大到 days + 1
            }
        }
        
        return low; // 返回最小等待天数
    }

    bool canMake(vector<int>& bloomDay, int days, int m, int k) {
        int bouquets = 0; // 制作的花束数量
        int flowers = 0; // 当前花束中的花朵数量
        int length = bloomDay.size();
        for (int i = 0; i < length && bouquets < m; i++) {
            if (bloomDay[i] <= days) {
                flowers++; // 符合开放条件的花朵数量递增
                if (flowers == k) { // 达到花束大小
                    bouquets++; // 制作的花束数量递增
                    flowers = 0; // 重置当前花束中的花朵数量
                }
            } else {
                flowers = 0; // 当前花朵无法用于制作花束，重置数量
            }
        }
        
        return bouquets >= m; // 制作的花束数量是否达到目标
    }
};

lc1011.在D天内送达包裹的能力–中等

题目描述

传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。

传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量（weights）的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。

返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。

示例 1：

输入：weights = [1,2,3,4,5,6,7,8,9,10], days = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10

请注意，货物必须按照给定的顺序装运，因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。 

示例 2：

输入：weights = [3,2,2,4,1,4], days = 3
输出：6
解释：
船舶最低载重 6 就能够在 3 天内送达所有包裹，如下所示：
第 1 天：3, 2
第 2 天：2, 4
第 3 天：1, 4

示例 3：

输入：weights = [1,2,3,1,1], days = 4
输出：3
解释：
第 1 天：1
第 2 天：2
第 3 天：3
第 4 天：1, 1

提示：

• 1 <= days <= weights.length <= 5 * 104
• 1 <= weights[i] <= 500

代码展示

class Solution {
public:
    int shipWithinDays(vector<int>& weights, int days) {
        int left = *max_element(weights.begin(), weights.end()); // 载重的下界
        int right = accumulate(weights.begin(), weights.end(), 0); // 载重的上界
        
        while (left < right) {
            int mid = left + (right - left) / 2; // 当前的运载能力猜测
            int daysNeeded = 1; // 当前载重下的天数
            int currentLoad = 0; // 当前运载的重量
            
            for (int weight : weights) {
                if (currentLoad + weight > mid) {
                    daysNeeded++; // 超过了当前运载能力，需要增加天数
                    currentLoad = 0; // 重置当前运载重量
                }
                currentLoad += weight; // 加载当前货物
            }
            
            if (daysNeeded <= days) {
                right = mid; // 可以在给定的天数内完成运输，缩小上界
            } else {
                left = mid + 1; // 需要更多的天数来完成运输，增加下界
            }
        }
        
        return left; // 返回最低的运载能力
    }
};

这段代码首先初始化左右指针，左指针 left 是所有货物中的最大重量，右指针 right 是所有货物总重量之和。然后，使用二分查找，在每一轮查找中，计算一个猜测的运载能力 mid，然后模拟按照这个运载能力来运送货物，计算需要的天数 daysNeeded。如果 daysNeeded 小于等于给定的天数 days，说明当前运载能力足够，可以在规定的天数内完成运输，所以将 right 缩小到 mid。如果 daysNeeded 大于 days，说明需要更多的天数来完成运输，因此将 left 增加到 mid + 1。最终，当 left 和 right 相等时，就找到了最低的运载能力，返回 left 即可。这个运算过程的时间复杂度是 O(n * log(sum(weights)))，其中 n 是货物的数量。

lc911.在线选举–中等

题目描述

给你两个整数数组 persons 和 times 。在选举中，第 i 张票是在时刻为 times[i] 时投给候选人 persons[i] 的。

对于发生在时刻 t 的每个查询，需要找出在 t 时刻在选举中领先的候选人的编号。

在 t 时刻投出的选票也将被计入我们的查询之中。在平局的情况下，最近获得投票的候选人将会获胜。

实现 TopVotedCandidate 类：

• TopVotedCandidate(int[] persons, int[] times) 使用 persons 和 times 数组初始化对象。
• int q(int t) 根据前面描述的规则，返回在时刻 t 在选举中领先的候选人的编号。

示例：

输入：
["TopVotedCandidate", "q", "q", "q", "q", "q", "q"]
[[[0, 1, 1, 0, 0, 1, 0], [0, 5, 10, 15, 20, 25, 30]], [3], [12], [25], [15], [24], [8]]
输出：
[null, 0, 1, 1, 0, 0, 1]

解释：
TopVotedCandidate topVotedCandidate = new TopVotedCandidate([0, 1, 1, 0, 0, 1, 0], [0, 5, 10, 15, 20, 25, 30]);
topVotedCandidate.q(3); // 返回 0 ，在时刻 3 ，票数分布为 [0] ，编号为 0 的候选人领先。
topVotedCandidate.q(12); // 返回 1 ，在时刻 12 ，票数分布为 [0,1,1] ，编号为 1 的候选人领先。
topVotedCandidate.q(25); // 返回 1 ，在时刻 25 ，票数分布为 [0,1,1,0,0,1] ，编号为 1 的候选人领先。（在平局的情况下，1 是最近获得投票的候选人）。
topVotedCandidate.q(15); // 返回 0
topVotedCandidate.q(24); // 返回 0
topVotedCandidate.q(8); // 返回 1

提示：

• 1 <= persons.length <= 5000
• times.length == persons.length
• 0 <= persons[i] < persons.length
• 0 <= times[i] <= 109
• times 是一个严格递增的有序数组
• times[0] <= t <= 109
• 每个测试用例最多调用 104 次 q

代码展示

为了解决这个问题，可以使用前缀和和二分查找的方法来快速找到在时刻 t 领先的候选人的编号。

首先，我们需要创建一个前缀和数组，用于记录每个时刻对应的候选人的得票数。然后，在查询时，可以使用二分查找找到时刻 t 在 times 数组中的位置，然后查找该位置对应的前缀和数组中的候选人编号，这个编号就是在时刻 t 领先的候选人。

以下是具体的代码实现：

class TopVotedCandidate {
public:
    TopVotedCandidate(vector<int>& persons, vector<int>& times) {
        int n = persons.size();
        leadingPerson.resize(n);
        prefixVotes.resize(n);
        vector<int> votesCount(n, 0);
        
        int maxVotes = 0;
        for (int i = 0; i < n; i++) {
            int person = persons[i];
            votesCount[person]++;
            if (votesCount[person] >= maxVotes) {
                maxVotes = votesCount[person];
                leadingPerson[i] = person;
            } else {
                leadingPerson[i] = leadingPerson[i - 1];
            }
            prefixVotes[i] = leadingPerson[i];
        }
        
        this->times = times;
    }
    
    int q(int t) {
        int index = binarySearch(t);
        return prefixVotes[index];
    }
    
private:
    vector<int> leadingPerson;
    vector<int> prefixVotes;
    vector<int> times;
    
    int binarySearch(int t) {
        int left = 0;
        int right = times.size() - 1;
        
        while (left < right) {
            int mid = left + (right - left + 1) / 2;
            if (times[mid] <= t) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        
        return left;
    }
};

在构造函数中，我们首先计算了每个时刻的领先候选人并存储在 leadingPerson 数组中。然后，我们将该数组复制到 prefixVotes 数组中，以便在查询时快速获取领先的候选人。在查询函数 q 中，我们使用二分查找来找到时刻 t 对应的位置，并返回对应的候选人。

lc875.爱吃香蕉的珂珂–中等

题目描述

珂珂喜欢吃香蕉。这里有 n 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 h 小时后回来。

珂珂可以决定她吃香蕉的速度 k （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 k 根。如果这堆香蕉少于 k 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉。

珂珂喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 h 小时内吃掉所有香蕉的最小速度 k（k 为整数）。

示例 1：

输入：piles = [3,6,7,11], h = 8
输出：4

示例 2：

输入：piles = [30,11,23,4,20], h = 5
输出：30

示例 3：

输入：piles = [30,11,23,4,20], h = 6
输出：23

提示：

• 1 <= piles.length <= 104
• piles.length <= h <= 109
• 1 <= piles[i] <= 109

代码展示

这个问题可以使用二分查找来解决。我们可以在可能的速度范围内进行二分查找，找到使得珂珂可以在 h 小时内吃掉所有香蕉的最小速度 k。

以下是具体的代码实现：

class Solution {
public:
    int minEatingSpeed(vector<int>& piles, int h) {
        int left = 1; // 最低速度
        int right = *max_element(piles.begin(), piles.end()); // 最高速度
        
        while (left < right) {
            int mid = left + (right - left) / 2; // 当前猜测的速度
            if (canEatAll(piles, mid, h)) {
                right = mid; // 可以在规定时间内吃完，减小速度
            } else {
                left = mid + 1; // 需要更多时间，增加速度
            }
        }
        
        return left; // 返回最小速度
    }
    
private:
    bool canEatAll(vector<int>& piles, int speed, int h) {
        int hoursNeeded = 0;
        for (int pile : piles) {
            hoursNeeded += (pile + speed - 1) / speed; // 使用向上取整来计算小时
        }
        return hoursNeeded <= h;
    }
};

在这段代码中，我们首先初始化左右指针，左指针 left 是最低速度 1，右指针 right 是堆中最多香蕉的数量。然后，在每一轮二分查找中，我们计算当前速度 mid 下是否可以在规定时间内吃完所有香蕉，这是通过 canEatAll 函数来计算的。如果可以，就缩小右边界，如果不能，就增加左边界。最终返回左指针 left 即可。