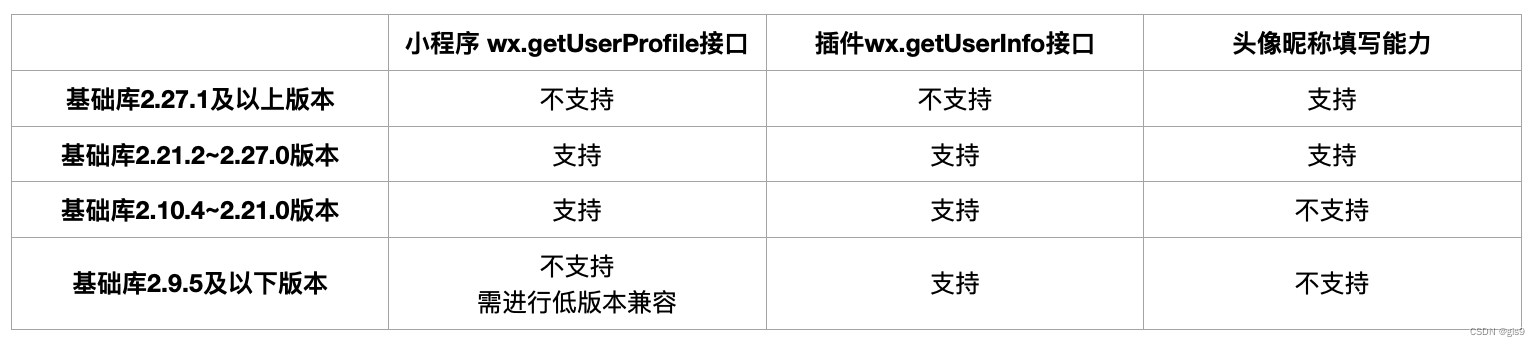
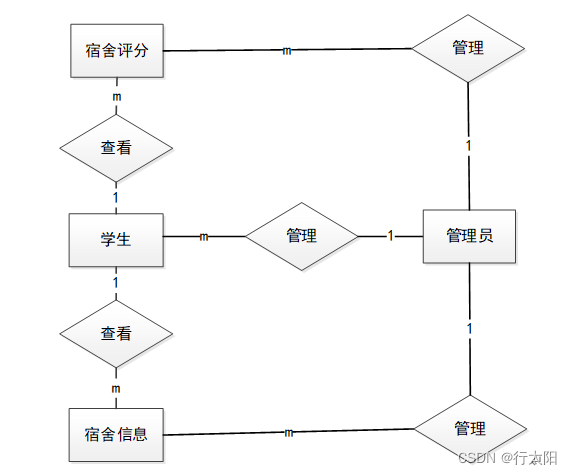
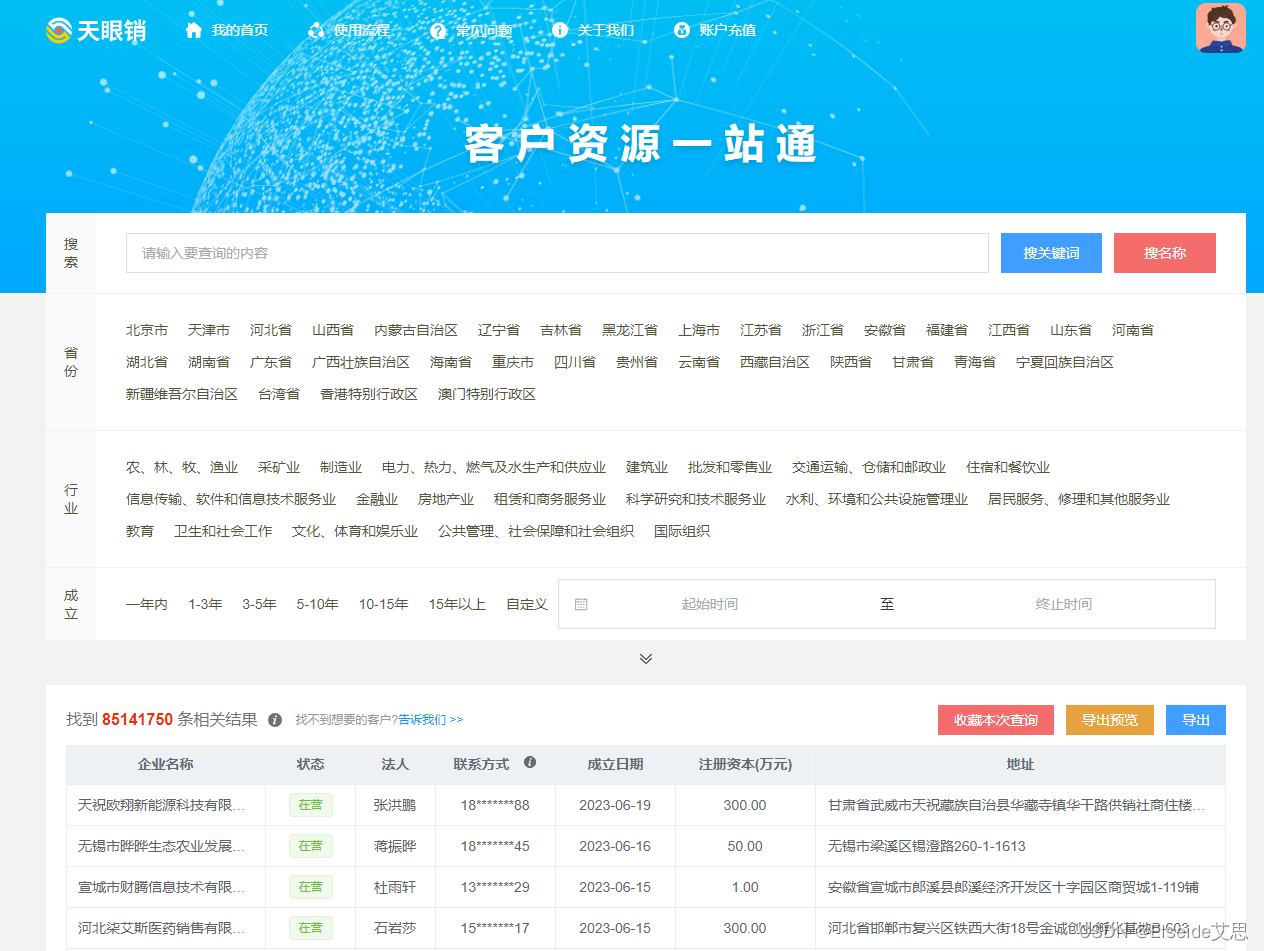
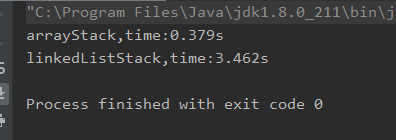
一、题目描述与要求

二叉搜索树的后序遍历序列_牛客题霸_牛客网 (nowcoder.com)

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true ,否则返回 false 。假设输入的数组的任意两个数字都互不相同。

数据范围： 节点数量 0≤n≤1000 ，节点上的值满足 1≤val≤105 ，保证节点上的值各不相同
要求：空间复杂度 O(n) ，时间时间复杂度 O(n2)

提示：

1.二叉搜索树是指父亲节点大于左子树中的全部节点，但是小于右子树中的全部节点的树。

2.该题我们约定空树不是二叉搜索树

3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历

4.参考下面的二叉搜索树，示例 1

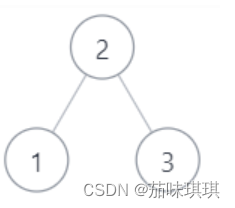
示例

示例1：

输入：[1,3,2]

返回值：true

说明：是上图的后序遍历 ，返回true

示例2：

输入：[3,1,2]

返回值：false

说明：不属于上图的后序遍历，从另外的二叉搜索树也不能后序遍历出该序列 ，因为最后的2一定是根节点，前面一定是孩子节点，可能是左孩子，右孩子，根节点，也可能是全左孩子，根节点，也可能是全右孩子，根节点，但是[3,1,2]的组合都不能满足这些情况，故返回false

示例3：

输入：[5,7,6,9,11,10,8]

返回值：true

---

二、解题思路

根据题目描述我们需要根据所给出的后序遍历序列来判断其是否是一个二叉搜索树。【二叉搜索树的特性是，左子树都比根结点小，右子树都比根结点大】

后序遍历的结果是按照“左子树——右子树——根结点”遍历的。

这个题的解题思路在于怎么去判断左子树与右子树是否合理，也就是是否比根结点小/大。所以核心在于我们要以根结点为基准对这个序列进行判断。

因而我们可以将这个序列翻过来遍历，这样就成了“根结点——右子树——左子树”的顺序，我们从根节点开始将其压入栈，后面对序列进行遍历，在找到比根结点小的结点以前（也就是把右子树遍历完）把每个结点都入栈，一旦找到比当前根结点小的结点（代表开始遍历左子树），将栈顶弹出，更新root【一开始root是无穷大，这是为了遍历完右子树】，然后继续判断，直至将序列遍历完了，则返回true。一旦在遍历的过程中，在更新了root之后，发现有结点比根结点大（此时应该是左子树，应该比root小），则说明这颗树不符合二叉搜索树，返回false。

首先判断是否为空树，空树直接返回false；

然后初始化root为无穷大（作为是否遍历完右子树的标志）；

然后对所给序列进行逆序遍历，每次循环都将当前结点与root进行比较（在root更新前，右子树还没遍历完，root更新后发现有未访问结点比root大则不符合二叉树性质）；

然后判断栈是否为空并且栈顶元素是否大于当前结点（栈顶元素最开始是根结点，所以一旦找到比根结点小的结点，则说明右子树遍历完成，更新root，同时利用while循环出栈，一直到找到当前结点的父节点）；

然后把当前元素压入栈中；

结束循环后返回true即可。

---

三、具体代码

#include <climits>
#include <cmath>
class Solution {
public:
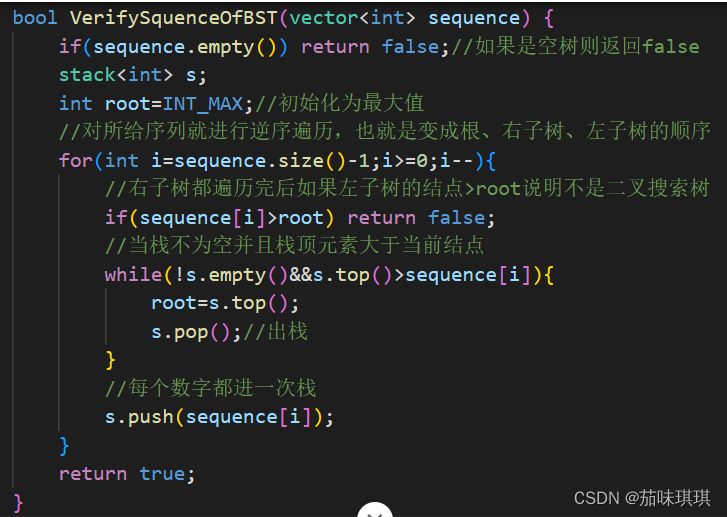
    bool VerifySquenceOfBST(vector<int> sequence) {
        if(sequence.empty()) return false;//如果是空树则返回false
        stack<int> s;
        int root=INT_MAX;//初始化为最大值
        //对所给序列就进行逆序遍历，也就是变成根、右子树、左子树的顺序
        for(int i=sequence.size()-1;i>=0;i--){
            //右子树都遍历完后如果左子树的结点>root说明不是二叉搜索树
            if(sequence[i]>root) return false;
            //当栈不为空并且栈顶元素大于当前结点
            while(!s.empty()&&s.top()>sequence[i]){
                root=s.top();
                s.pop();//出栈
            }    
            //每个数字都进一次栈
            s.push(sequence[i]);
        }
        return true;
    }
};