并查集

定义

🚀在一些应用问题中，需要将n个不同的元素分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中，要反复用到查询某一个元素属于哪个集合的运算。适合描述这类问题的抽象数据结构叫做并查集。

🚀由于每个集合就是一颗树形结构，一个并查集内存在多个集合，所以并查集是一个森林。
🚀通常用数组来充当这种数据结构，采用双亲表示法的方式，即子节点存储父节点的指针。

举例说明

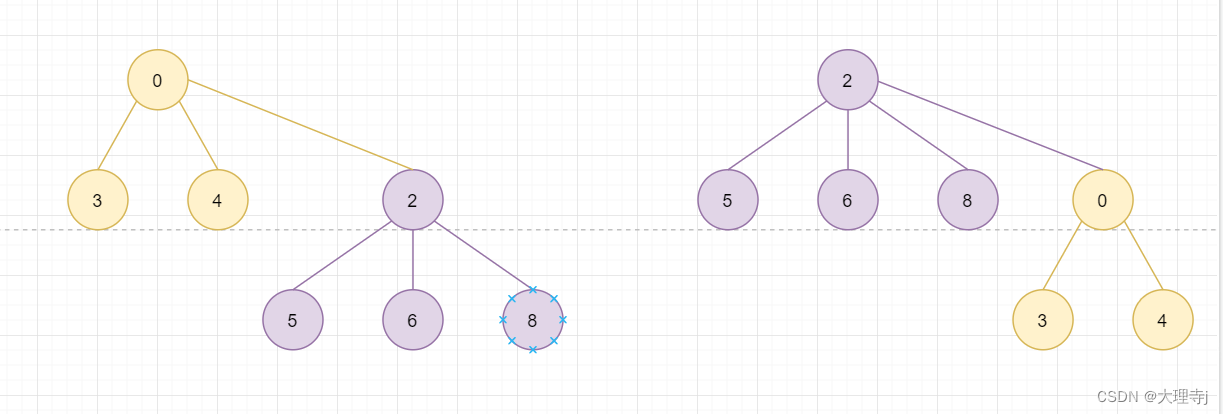
🚀例如，有10名同学，它们的编号分别为0-9，它们来自三个班级（1班，2班，3班），其中0，3，4号同学来自一班，1，7，9同学来自2班，2，5，6，8号同学来自3班。

初始结构：每个元素各自独立为一个集合。

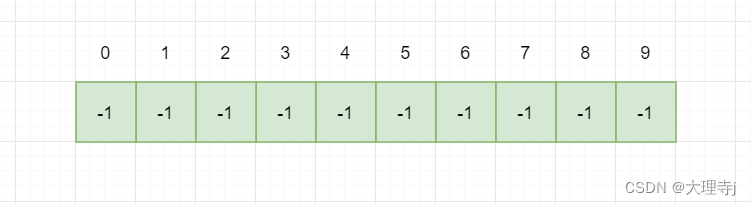
元素的合并：相同班级的同学合并为同一个集合。

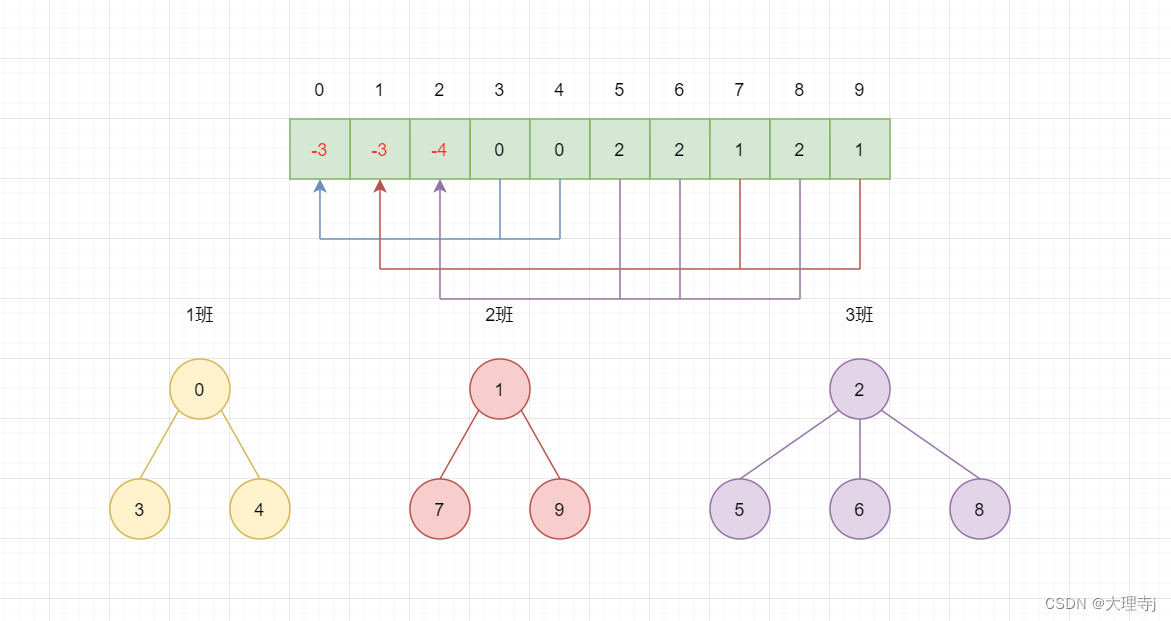
🚀合并规则：

将子节点的数据加到父节点的数据中，将字节点的数据改为父节点的指针。这样父节点中的数据的绝对值就是此集合中元素个数，各个子节点存储的都是指向父节点的指针。

🚀合并的优化：

在合并时，最好将集合内元素数量较少的集合合并到集合内元素数量多的集合。这样在查找某个元素属于哪个集合时可以减少时间消耗。例如，将1班和3班合并，优先是将1班合并到3班，这样第三层的结点数量比较少，相比于将3班合并到1班。

查找某个元素属于哪个集合

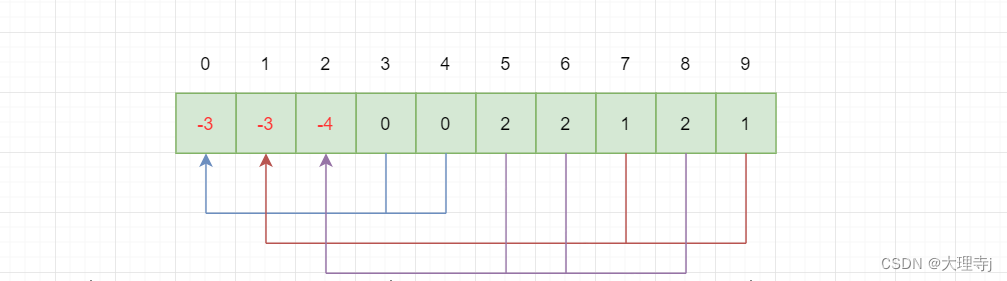
🚀例如查找n号下元素属于哪个集合，只需要判断n号位置的元素是否为负数，如果为负数说明n号位置就是这个集合的根节点(用根节点的下标来标识集合)，如果不是负数就顺着父节点向上访问，直到根节点为止。

代码实现

#pragma once

#include <vector>
#include <iostream>

/*
*					并查集
* 1.核心采用双亲表示法，孩子结点存储的是父节点的下表
* 2.采用类似堆的结构表示---在数组中存储
*/
class UnionFindSet {
private:
	std::vector<int> _ufs;
public:
	UnionFindSet(size_t n) :_ufs(n,-1) {}
	int FindRoot(int x) {
		int parent = x;
		//一直向上找到存储负数的结点
		while (_ufs[parent] >= 0) {
			parent = _ufs[parent];
		}
		return parent;
	}
	void Union(int x1, int x2) {
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		if (root1 == root2) { return; } //本身就在一个集合当中
		if (abs(_ufs[root1]) < abs(_ufs[root2])) {
			std::swap(root1, root2);
		}
		_ufs[root1] += _ufs[root2];     //将root2结点的数据加到root1结点的数据上
		_ufs[root2] = root1;            //将root2结点的数据修改为root1(根结点的下标)
	}
	size_t SetSize() const {
		size_t cnt = 0;
		for (auto& e : _ufs) {
			if (e < 0) { cnt++; }  //结点数据为0的就表示为根结点，能够代表一个集合
		}
		return cnt;
	}
	bool InSet(int x1, int x2)  {
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		return root1 == root2;
	}
};

路径压缩

🚀在经过多次集合合并时，可能会出现某个集合的树形结构深度很深，从而导致查询某个元素的集合时时间消耗比较大，所以可以对树形结构的路径进行压缩。

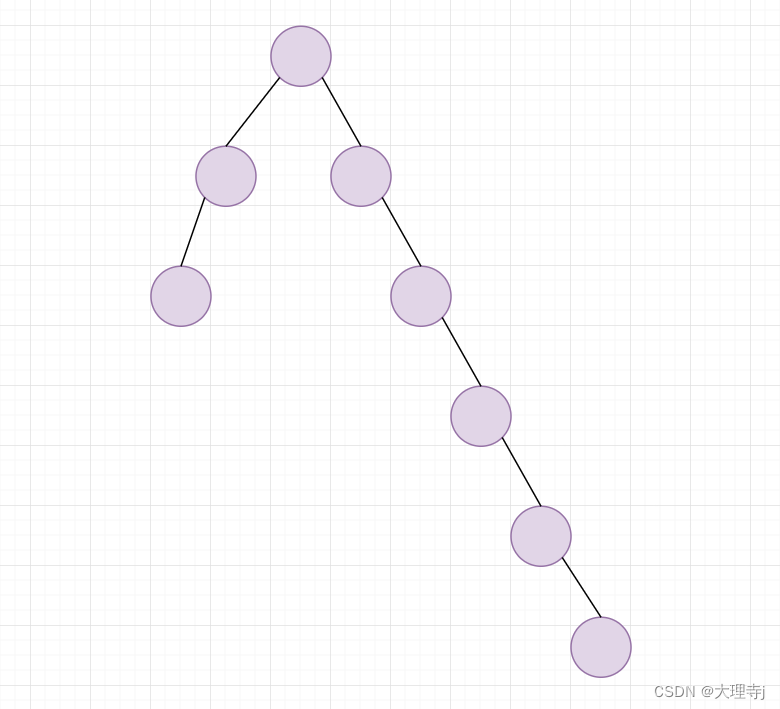
上图只是个示例，通常来说数据量很大的时候才需要路径压缩。

压缩策略：

在查找某个元素属于哪个集合时进行路径的压缩，在找到某个元素的根节点后不着急返回，而是依次将此路径上的该元素的父节点合并到根结点处，完成路径压缩。这样下次再查找某个元素属于哪个集合时，就可以提高效率。

int FindRoot(int x) {
	int parent = x;
	//一直向上找到存储负数的结点
	while (_ufs[parent] >= 0) {
		parent = _ufs[parent];
	}
	//核心代码
	int cur = x;
	while (_ufs[cur] >= 0) {
		int tmp = cur;
		cur = _ufs[cur];
		_ufs[tmp] = parent;
	}
	return parent;
}

Kruskal

最小生成树
🚀最小生成树就是在图的所有生成树中找出各个路径权值和最小的那个路径。

算法原理

🚀克鲁斯卡尔算法是求图的最小生成树的一个经典算法，其采用全局贪心的思想，每次都去选权值最小的边(可以将所有边放在一个小根堆中每次获取堆顶元素)去构成最小生成树(不能重复选取某一个边)，但是这种贪心方式可能会造成环路的产生，所以在每选一个边之前都要判断一下选取这个边后会不会构成环路。而判环的这个步骤使用并查集是非常适合的，可以将已经选取出来的构成最小生成树的顶点放在一个集合S中，在添加某个边时，如果这个边的两个顶点均位于集合S中，说明构成了环路这条边是不能选取的。

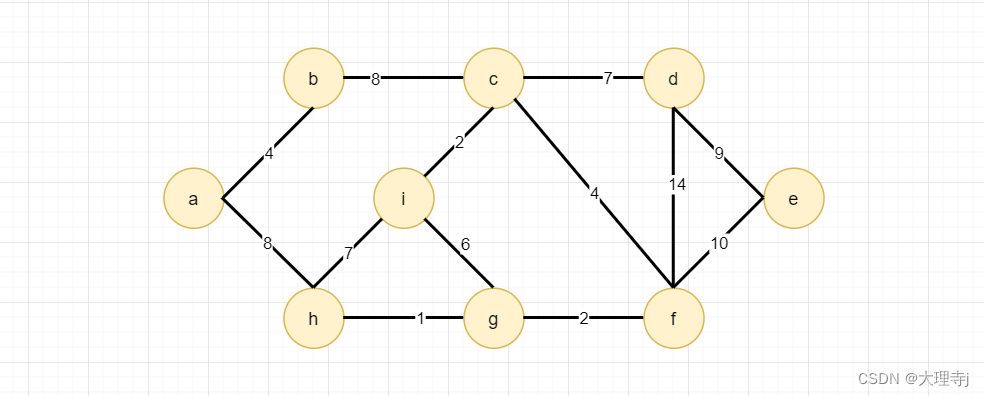
选取边的过程：

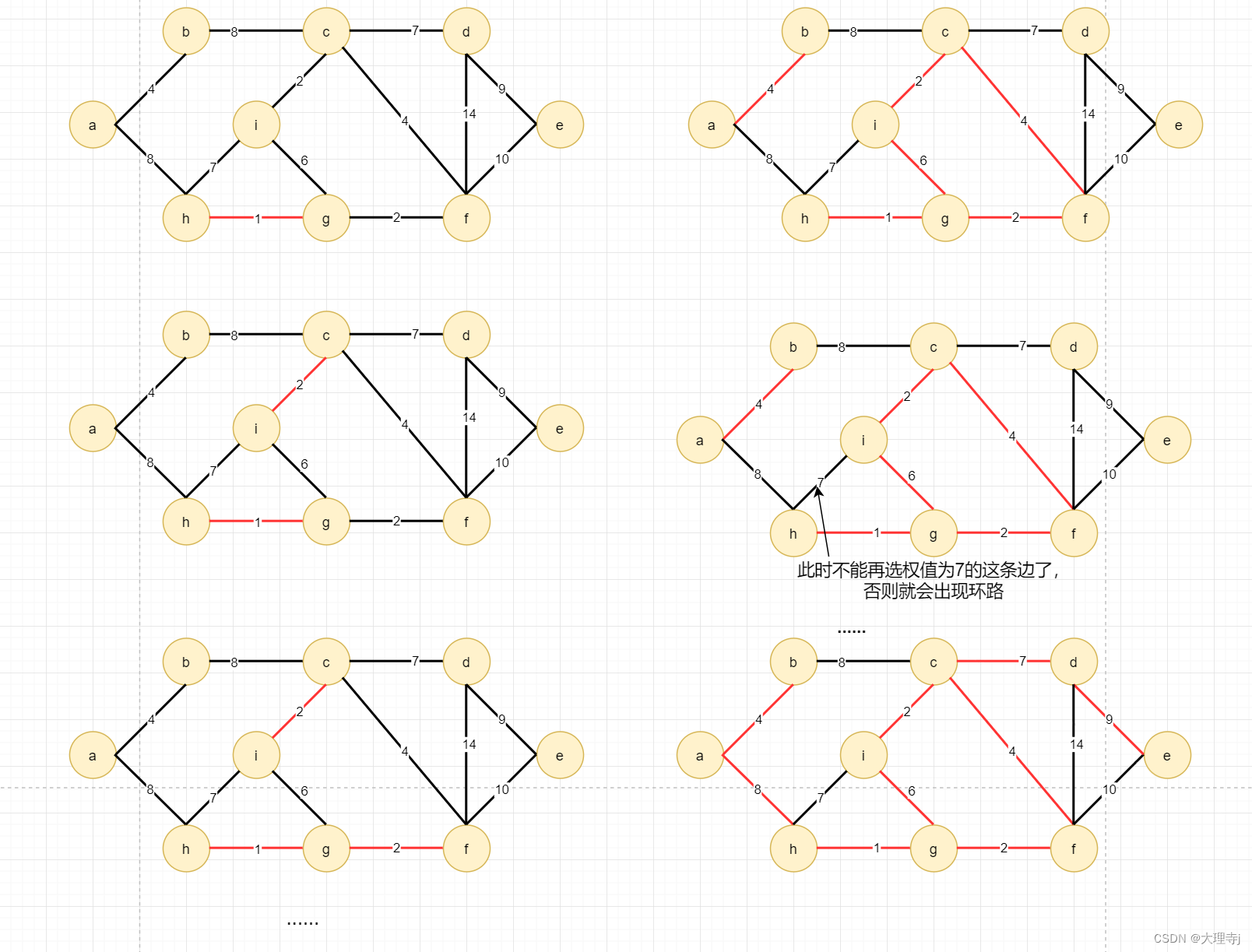
🚀最小生成树的结果并不唯一，例如上图中有两个权值为8的边，上面的选法中是选取了ah这条边，选取bc这条边也是没有问题的。

代码实现

struct Edge {
	size_t _srci;
	size_t _dsti;
	W _weight;

	Edge(size_t srci,size_t dsti,const W& weight) :_srci(srci),_dsti(dsti),_weight(weight) 
	{}
	bool operator > (const Edge& e) const {
		return _weight > e._weight;
	}
};

W Kruskal(self& min_tree) {
	size_t n = _vertex.size();
	min_tree._vertex = _vertex;
	min_tree._index_map = _index_map;
	//初始化矩阵
	min_tree._matrix.resize(n, std::vector<W>(n, W_MAX));
	//开始计算最小生成树
	std::priority_queue<Edge,std::vector<Edge>,std::greater<Edge>> pq;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (i < j && _matrix[i][j] != W_MAX) { 
			//i<j在无向图中避免同一条边添加两次
				pq.push(Edge(i, j, _matrix[i][j]));
			}
		}
	}
	W total = W();//记录权值和
	size_t size = 0;//记录挑选出的边的个数
	UnionFindSet ufs(n);
	while (size < n - 1 && !pq.empty()) {
		Edge eg = pq.top();
		pq.pop();
		if (ufs.InSet(eg._srci, eg._dsti) == false) {
			min_tree._AddEdge(eg._srci, eg._dsti, eg._weight);
			ufs.Union((int)eg._srci, (int)eg._dsti);
			total += eg._weight;
			++size;
		}
	}
	if (size != n - 1) {
		return W();
	}
	return total;
}

Prim

算法原理

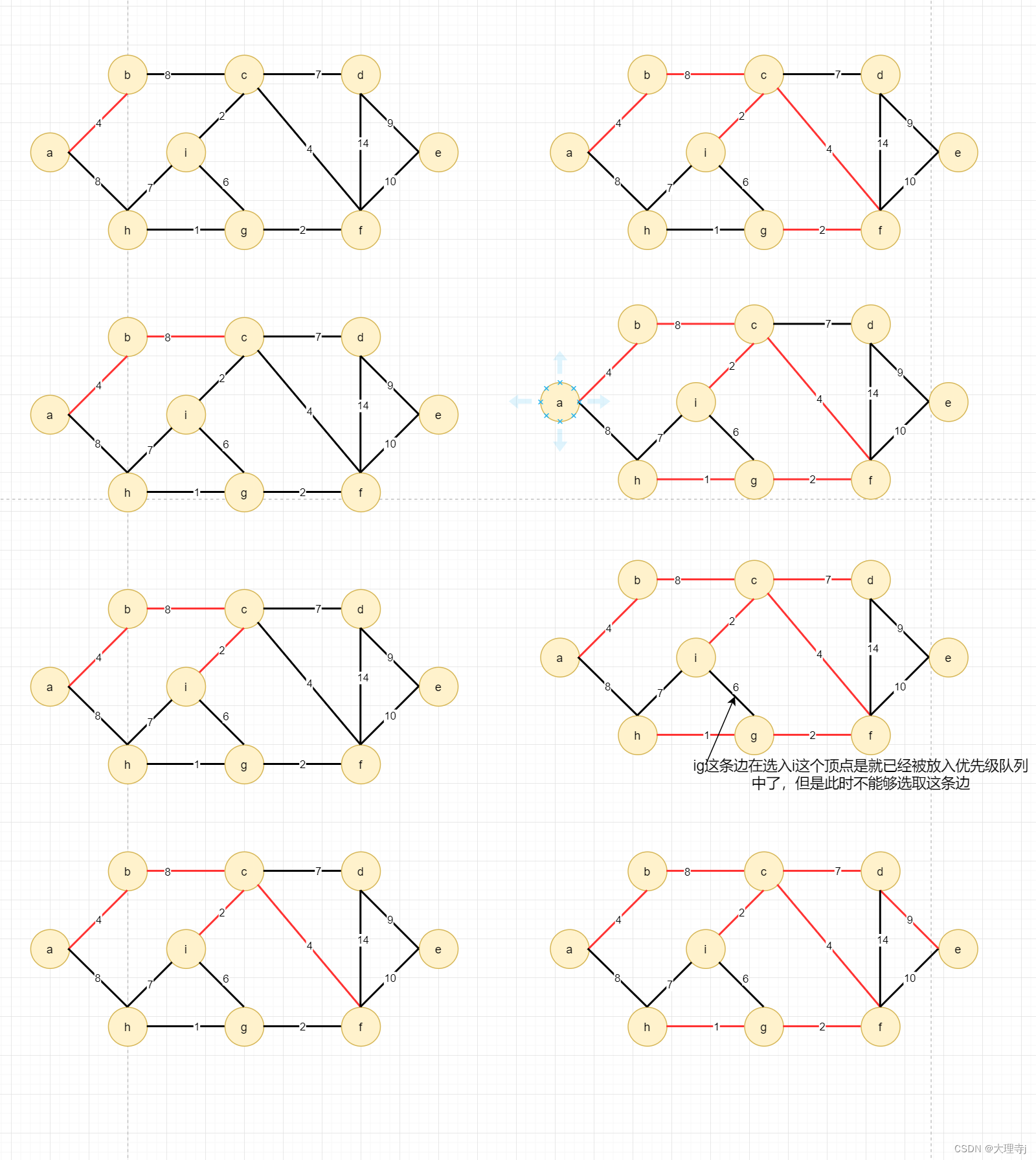
🚀Prim算法与Krunskal算法都是采用贪心的策略，但是Prim算法采用的是局部贪心的策略，在Prim算法中会将图的顶点分类到两个集合X，Y中，对于已经选入到最小生成树的边相连的顶点放在X集合中，没有选进最小生成树的顶点放入Y集合。而在贪心选取权值最小的边时，是在一个顶点位于X集合另一个顶点位于Y集合的所有边中去选择的。所以Prim算法需要指定一个起始顶点。当某个顶点被添加到X集合后，要将与其相连的边放入到优先级队列中，放入优先级队列的边也是有要求的就是它另一个顶点必须是在Y集合中的（如果采用优先级队列的方式存储边，仍然会出现环路情况，所以在选边的同时也要注意判环操作）

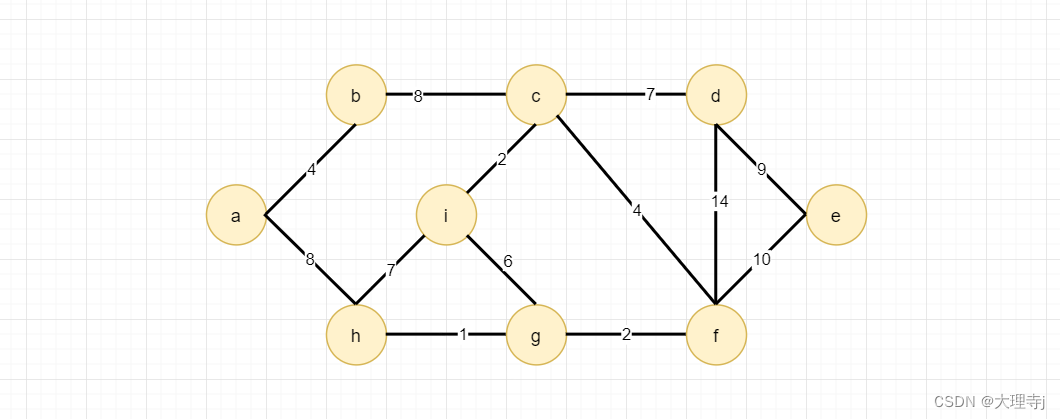
选取边的过程
假设起始顶点为a：

代码实现

W Prim(self& min_tree, const V& src) {
	size_t n = _vertex.size();
	min_tree._vertex = _vertex;
	min_tree._index_map = _index_map;
	//初始化矩阵
	min_tree._matrix.resize(n, std::vector<W>(n, W_MAX));
	//将所有的顶点划分为两个集合 X Y，已经选择的点放入X集合中，没有选择的点在Y集合中
	size_t srci = this->GetVertexIndex(src);
	std::vector<bool> X(n, false);
	std::vector<bool> Y(n, true);
	X[srci] = true;
	Y[srci] = false;
	//将与X集合中所有顶点相连的边存入优先级队列，以供贪心选择
	std::priority_queue<Edge, std::vector<Edge>, std::greater<Edge>> pq;
	for (size_t i = 0; i < n; ++i) {
		if (_matrix[srci][i] != W_MAX) {
			pq.push(Edge(srci, i, _matrix[srci][i]));
		}
	}
	
	size_t size = 0;
	W total_w = W();
	while (size < n - 1 && !pq.empty()) {
		Edge eg = pq.top();
		pq.pop();
		//防止选出的边构成环
		if (true == X[eg._dsti]) {
			continue;
		}
		X[eg._dsti] = true;
		Y[eg._dsti] = false;
		min_tree._AddEdge(eg._srci, eg._dsti, eg._weight);
		++size;
		total_w += eg._weight;
		//std::cout << _vertex[eg._srci] << "->" << _vertex[eg._dsti] << ":" << eg._weight << std::endl;
		//将以dsti点为起点的边加入到队列中
		for (size_t i = 0; i < n; i++) {
			//存在边且终点位于Y集合中
			if (_matrix[eg._dsti][i] != W_MAX && Y[i]) {
				pq.push(Edge(eg._dsti, i, _matrix[eg._dsti][i]));
			}
		}
	}
	if (size != n - 1) {
		return W();
	}
	return total_w;
}