2.1暂无

2.2 翻译答案
如图 P2.3 所示,视网膜图像中与点相对应的直径 x 是由类似的三角形得到的。即

得出 x = 0.085d。根据第 2.1 节中的讨论,并结合一些自由解释,我们可以将眼窝视为一个方形传感器阵列,拥有大约 337,000 个元素,这相当于一个大约 580×580 个元素的阵列。假设元素间距相等,则在 1.5 毫米长的直线上有 580 个元素和 579 个空间,共计 1,159 个。换句话说,如果一个点的直径 d<1.3×10-6 m,或者 d<15.3×10 m,眼睛就无法检测到这个点。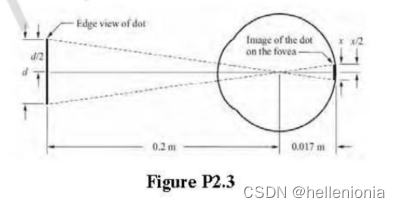

2.3 暂无

2.4 翻译答案
(a) 根据第 2.2 节中关于电磁波谱的讨论,观察物体所需的照明光源的波长必须与物体的 大小相同或更小。由于兴趣只取决于边界形状,而不取决于标本的其他光谱特性,因此远紫外光(波长为 0.001 微米或更小)的单一照明光源将能够探测到所有物体,而可辨别的最小细节将为 0.001 微米或更小,与照明光源的波长相同。要对标本成像,需要一个远紫外相机传感器。

2.5 翻译答案
(a) 图像的垂直(或水平)尺寸为 5 厘米或 50 毫米。因此,我们必须在 50 毫米内容纳 2048 行,即大约 41 行/毫米。线对是线对的一半,即每毫米约 20 个线对。

![]()
2.6 翻译答案
根据图 2.3 中的几何图形,(7 mm)(35 mm)=(z)(500 mm) 或 z = 100 mm。因此,目标尺寸为边长 100 毫米。每行共有 1024 个元素,因此 1 行的分辨率为 1024100 = 10 个元素/毫米。对于线对,我们除以 2,得出 5 lp/mm。

2.7 暂无

2.8 翻译答案
让 D 表示从摄像机镜头中心到成像区域的距离,假设为 1 米;让 H 表示成像区域的高度,假设为 0.5 米;让 L 表示镜头的焦距,假设为 200 毫米。我们希望找到 d,即在透镜焦平面上成像区域的高度(这将是所需 CCD 芯片的最小尺寸)。那么,根据图 2.3 中的几何图形,(H/D) = (d/L) 或
d =(LH)/D =(200 mm)(500 mm)/1000 mm = 100 mm
因此,成像区域的大小为 100 平方毫米。我们需要的分辨率是每毫米 5 个线对,即垂直(和水平)方向上每毫米 10 个像素。由于 d= 100 毫米,我们需要在图像的每条垂直线上检测到(10 像素/毫米)(100 毫米)=1000 像素。

2.9 翻译答案
(a) 在一幅 8 位,1024×1024 的图像中,数据总量(包括起始位和停止位)为 (1024) ×(8+2) 位。通过 3 M 波特调制解调器传输 500 幅此类图像所需的总时间为
传输时间 = 500x(1024)^2×(10)/(3 ×10^6)= 1,748 秒。

2.10 翻译答案
宽高比为 16/9,垂直方向的分辨率为 1125 行(或垂直方向的分辨率为 1125 像素)。系统每隔 1/30 秒就会 "绘制 "一幅完整的 1125×2000 的 8 位图像,包括红、绿和蓝分量图像。两小时共有 7200 秒,因此在这一时间间隔内产生的数字数据总量为 (1125)(2000)(8)(30)(3)(7200)=1.166×10 位,或 1.458×1012 字节(即约 1.5 TB)。

2.11 翻译答案
(a) 根据问题陈述、
x +M(y+Nz)= s
将方程两边相对于 M 进行 "调制",得到
x = s mod M
这里我们利用了第一个等式左边的事实,即所有量都是整数,整数加 M 的整数倍的余数等于第一个整数。

2.12 翻译答案
有关图像由以下公式给出

图像的横截面如图 P2.12(a)所示。如果使用 k 比特对强度进行量化,则会出现图 P2.14(b)所示的情况,即 △G =(255+ 1)/2" 。由于假定眼睛可以检测到 8 级强度的突然变化,因此 AG=8 =256/2',即 k =5。换句话说,32 个或更少的强度等级将产生可见的虚假轮廓。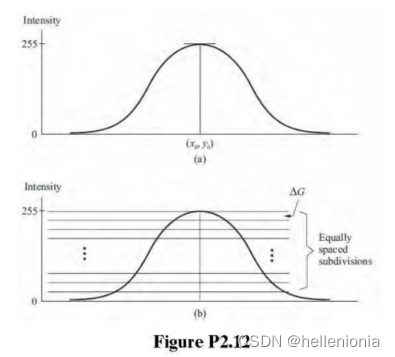
2.13 暂无


2.14 翻译答案
设 p 和 q 如图 P2.14 所示、
(a) Sand Sz 不是 4 连接的,因为 q 不在集合 N4(p) 中。


2.15 翻译答案
如图 P2.15 所示,解决这一问题的方法包括定义所有可能的邻域形状,以便从对角线线段到相应的 4 连接线段。然后,每次在边界中遇到对角线段时,算法只需寻找适当的匹配。
2.16 暂无

2.17 暂无
![]()

2.18 翻译答案
(a) 当 V= {0,1} 时,在 p 和 q 之间不存在一条 4 路径,因为从 p 到 q 不可能沿着既 4 相邻又有来自 V 的值的点走。
图 P2.18(a) 显示了这一条件;不可能到达 q。
最短的 8 路径如图 P2.18(b) 所示,其长度为 4。
最短 m 路径(虚线所示)的长度为 5。
在这种情况下,这两条最短路径都是唯一的。

2.19 翻译答案
(a) 图 P2.19 显示了坐标为 (x,y) 的点 p 与坐标为 (s,t) 的点 q 之间的最短 4 路径,假设路径上的所有点都来自 V。 路径总长度为 |r一s|+ly-t4,这就是公式(2-20)中给出的 D ,距离的定义。当路径的长度为 x-s己+ly一4 时,D ,距离显然等于最短的 4 路径的长度。当我们可以沿着一条路径从 p 到 q 时,就会出现这种情况,这条路径的元素(1)来自 V,(2)以这样的方式排列,即我们可以通过在最多两个方向(例如右转和向上)转弯来横穿从 p 到 q 的路径。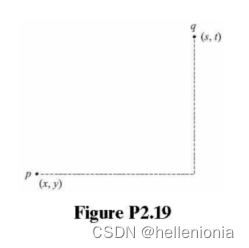

2.20 暂无
2.21 暂无

2.22 翻译答案
参照公式 (2-22) 和 (2-23),让 H 表示求和算子,让 S、和 S,表示两个大小相同的不同小子图像区域,让 S,+S,表示 S、和 Sz 中元素的相应元素和,如第 2.6 节所述。算子 H 计算一个邻域中像素值的总和,因此可以得到一个给定邻域的标量。 那么,H(aS,+ bS,)的含义是:(1)将每个子图像区域中的像素乘以所示常数;(2)将 aS 和 bS 中的像素值逐个相加(产生一个单一的子图像区域);(3)计算该单一子图像区域中所有像素的值之和,产生一个标量。然后我们可以写出
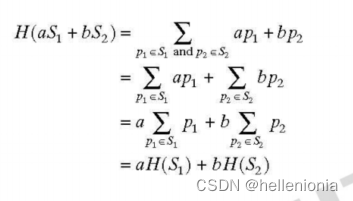
根据公式 (2-23),这表明 H 是一个线性算子。

2.23 翻译答案
(a) 加法: 公式 (2-23 ) 的左边为
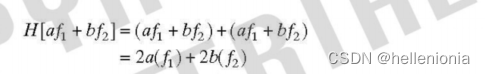
公式 (23 ) 的右边为
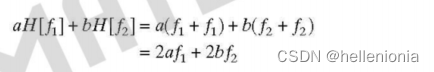
左右两边相等,因此求和算子是线性的。
(c) 乘法: 公式 (2-23) 的左边为

其中,f × f 是两个图像的元素乘积。公式(2-23)的右边是

左边不等于右边,因此乘法算子不是线性的。

2.24 暂无

2.25 翻译答案
k 幅图像的平均值为

而 k +1 幅图像的平均值为


2.26 翻译答案
(a) 根据公式 (2-26),在任意点 (x,y),
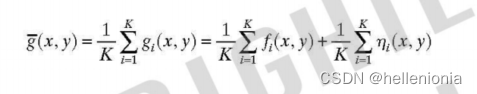
由于该方程适用于任意坐标 (x,y),我们可以去掉坐标来简化符号。

换句话说,噪声图像是通过在同一幅图像上添加噪声而形成的。不同图像中的噪声会发生变化,但 f 却保持不变。此外,噪声的均值为零,所以 E(n}=0。 因此,可以得出 Elg}= f,或 E(g(x,y)= f(x,y),这证明了公式(2-27)的有效性。

2.27 翻译答案
在我们的工作中,8 位图像的强度值范围是 [0,255]。
对这一范围内的值进行减法,可覆盖 [-255,255] 的范围。
8 位无法覆盖这个范围,但问题说明中指出,减法的结果也必须用 8 位表示,因此仅限于 [0,255] 这个范围。这就意味着,任何 2 个像素的减法结果如果为负数,都将被剪切为 0。从图像 a(x,y)到图像 b(x,y)的重复减法过程可以表示为
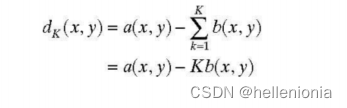
其中,dg(x, y) 是经过 K 次减法后得到的差分图像。由于图像减法是一种无元素操作(见第 2.6 节),我们可以将注意力集中在图像中任何相应像素对的减法上。我们已经说过,负值的结果会以 0 为界限。一旦得到 0 的结果,它就会保持不变,因为从 0 减去任何非负值都是一个负值,同样也会以 0 为界限。 同样,b(x,y,)=0 的任何位置 (xo,y% ) 都会产生结果dx (xo;y%)= a(xo,y%)。在本问题中,减法的最大次数为 255 次,对应于 a(x,y) 为 255、b(x,y) 为 1 的位置条件。 因此,我们从前面的讨论中得出结论,从另一幅图像中重复减去一幅图像(并以 8 比特表示结果),将得到一幅差分图像,在 b(x,y)中不为零的位置,其分量为 0,在 b(x,y)中为 0 的位置,其分量等于 a(x,y)的原始值。

2.28 翻译答案
让 g(x, y) 表示黄金图像,让 f(x, y) 表示在系统日常运行过程中获取的任何输入图像。通过减法进行变化检测的基础是计算差分(x, y)=g(x,y)- f(x,y)。由此得到的图像 d(x, y) 可用于两种基本的变化检测方法。在这种情况下,如果 d(x,y)中的所有像素都在指定的阈值范围 [Tmim.Tmax] 内,我们就认为 f(r,y)与黄金图像 "足够接近",其中 Tmm 为负值,Tmax.为正值。通常情况下,负差和正差都使用相同的阈值,因此我们有一个范围 [-T. T ],d(x,y) 的所有像素都必须在这个范围内,这样 f(x, y) 才能被认为是可接受的。第二种主要方法是对 lad(x, y) 中的所有像素求和,然后将和与阈值 Q 进行比较。这种测试方法要粗糙得多,因此我们将重点讨论第一种方法。
要进行基于差值的检测,有三个基本因素需要严格控制:(1) 正确的配准;(2) 受控的光照;(3) 足够低的噪声水平,使差值不会受到噪声变化的明显影响。第一个条件基本上解决了在相应像素之间进行比较的要求。
两个图像可以是完全相同的,但如果它们相互之间有位移,那么比较它们之间的差异就没有意义了。
受控照明("照明 "并不局限于可见光)显然非常重要,因为照明的变化会极大地影响差分图像中的数值。例如,产品可以有一个或多个严格控制颜色的小块,整个图像中像素的强度(甚至颜色)将根据正在处理的图像中块的实际与预期强度和颜色进行修改。
最后,差分图像的噪点含量必须足够低,这样才不会对黄金图像和输入图像之间的比较产生实质性影响。良好的信号强度可以大大降低噪声的影响。
上述基本主题有许多变体。例如,可以采用比逐个像素阈值比较更复杂的测试形式来实现额外的智能。这方面经常使用的一种技术是将黄金图像细分为不同的区域,并根据预期的区域内容在每个区域执行不同(通常不止一次)的测试。

2.29 翻译答案


2.30 翻译答案


2.31 翻译答案
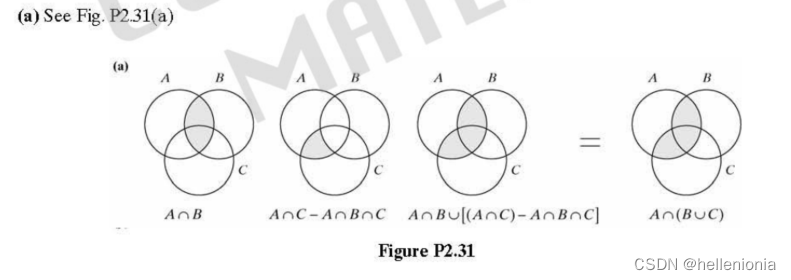

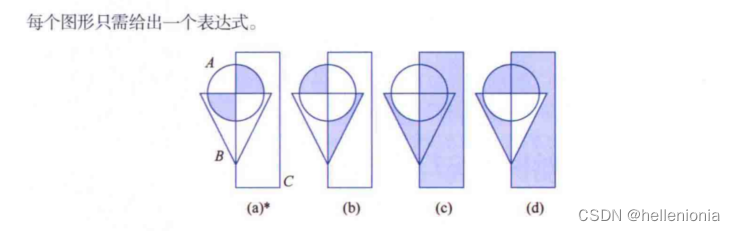
2.32 翻译答案
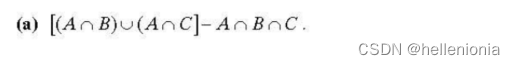

2.33 翻译答案
(a) 我们必须证明,在 "小于或等于 "的关系中,以下三个性质是成立的。
反身性: 换句话说,任何实数都等于它本身。
传递性: 对于任意三个实数 a、b 和 c,如果 a 小于或等于 b,并且 b 小于或等于 c,那么 a 小于或等于 c。
反对称性: 对于任意两个实数 a 和 b,如果 a 小于或等于 b,并且 b 小于或等于 a,那么 a 和 b 就是同一个数。
由于这三个性质都成立,所以集合 S 是 "小于或等于 "关系下的部分有序集合。
(b) 我们必须证明在 "小于等于 "关系下,反复性和反转性的性质成立。
反复性: 任何实数都不可能小于它本身,所以这个性质成立。
传递性: 对于任意三个实数 a、b 和 c,如果 a 小于 b,并且 b 小于 c,那么推论是 a 一定小于 c。
2.34 翻译答案
要解决这个问题,我们必须证明 "能被......整除 "的关系是反身的、传递的和对称的。
(a) 反身性:任何正整数都能被它自己整除(即问题陈述中的 k = 1),因此满足这个条件。

2.35 暂无

2.36 翻译答案
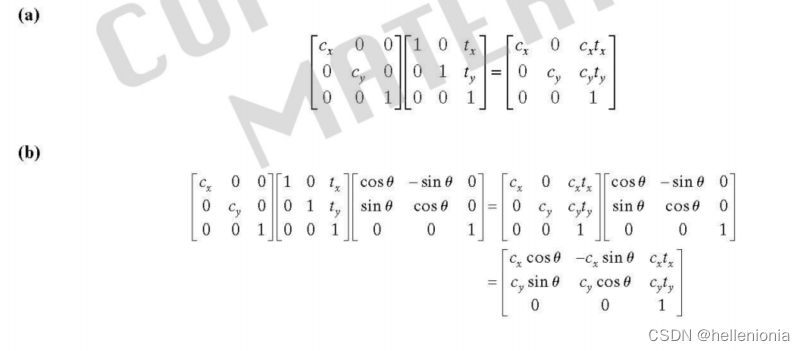

2.37 翻译答案
(a) 正向缩放变换为

相应的逆变换为

(d) 正向旋转变换为

相应的逆旋转变换为

(e) 复合平移/旋转变换为

相应的逆变换为

注意正向与反向复合变换中矩阵的顺序。
![]()

2.39 翻译答案
(a) 傅立叶变换核是可分的,因为

它是对称的,因为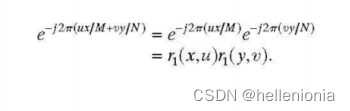

2.40 翻译答案
由式 (2-59) 和可分离核的定义可得

其中
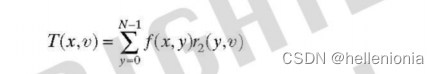
对于固定的 x 值,该方程被视为沿 f (x, y) 一行的一维变换。通过让 x 从 0 到 M -1 的变化,我们可以计算出整个数组 T(x,v)。然后,将这个数组代入上一个等式的最后一行,我们就得到了沿 T(x, o) 列的一维变换。换句话说,当核是可分离的,我们就可以沿着图像的行计算一维变换。然后,我们沿着中间结果的列计算一维变换,得到最终的二维变换 T(u,o)。我们先计算 f(x,y) 列的一维变换,再计算中间结果行的一维变换,就能得到相同的结果。
在第 4 章讨论 2-D 傅立叶变换时,这一结果将发挥重要作用。根据公式(2-61),二维傅里叶变换的计算公式为
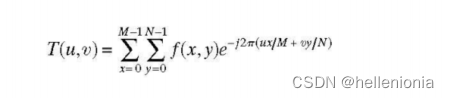
从问题 2.41 中我们知道,傅立叶变换核是可分离的,因此我们可以把这个式子写成

其中
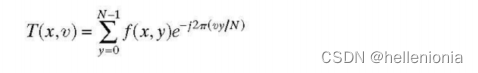
是沿 f(x,y) 行的一维傅立叶变换,设 x=0,1,2,... ,M -1.

2.41 暂无
【英文原版答案】