目录

差分数组-区间增减

和为K的子数组：前缀和 + 哈希表优化

除自身以外数组的乘积：前后缀区间

---

差分数组-区间增减

想对区间 nums[i..j] 的元素全部加 3，那么只需要让 diff[i] += 3，然后再让 diff[j+1] -= 3

和为K的子数组：前缀和 + 哈希表优化

var subarraySum = function(nums, k) {
    // 创建一个 Map 数据结构，用于存储前缀和及其出现的次数
    const mp = new Map();
    
    // 将前缀和为 0 的情况初始化为 1，表示第一个元素就是和为 0 的子数组
    mp.set(0, 1);

    // 初始化计数器 count 为 0，pre 为前缀和的累加值
    let count = 0, pre = 0;

    // 遍历数组 nums 中的每个元素
    for (const x of nums) {
        // 计算前缀和，即当前元素值与前面元素的和
        pre += x;

        // 如果 Map 中存在前缀和等于 (pre - k) 的记录，表示找到一个子数组的和为 k
        // 在 Map 中查找 (pre - k) 对应的次数，将次数加到计数器 count 上
        if (mp.has(pre - k)) {
            count += mp.get(pre - k);
        }

        // 更新 Map，将当前前缀和 pre 对应的次数加一
        if (mp.has(pre)) {
            mp.set(pre, mp.get(pre) + 1);
        } else {
            mp.set(pre, 1);
        }
    }

    // 返回最终的子数组和为 k 的个数
    return count;
};

除自身以外数组的乘积：前后缀区间

var productExceptSelf = function(nums) {
    const length = nums.length;
    const answer = new Array(length);

    // answer[i] 表示索引 i 左侧所有元素的乘积
    // 因为索引为 '0' 的元素左侧没有元素，所以 answer[0] = 1
    answer[0] = 1;
    for (let i = 1; i < length; i++) {
        answer[i] = nums[i - 1] * answer[i - 1];
    }

    // R 为右侧所有元素的乘积
    // 刚开始右边没有元素，所以 R = 1
    let R = 1;
    for (let i = length - 1; i >= 0; i--) {
        // 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
        answer[i] = answer[i] * R;
        // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
        R *= nums[i];
    }
    return answer;
};

小而美的算法技巧：前缀和数组 | labuladong 的算法笔记

位运算

异或：同为0，不同为1

异或运算 XOR：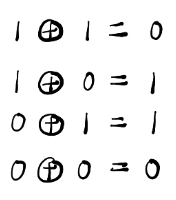

• 一个数和 0 做 XOR 运算等于本身：a⊕0 = a
• 一个数和其本身做 XOR 运算等于 0：a⊕a = 0
• XOR 运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b

136. 只出现一次的数字：除了某个元素只出现一次以外，其余每个元素均出现2次

将所有数字按照顺序做抑或运算，最后剩下的结果即为唯一的数字
时间复杂度：O(n)，空间复杂度：O(1)

/**
 * @param {number[]} nums
 * @return {number}
 */
var singleNumber = function(nums) {
    let ans = 0;
    for(const num of nums) {
        ans ^= num;
    }
    return ans;
};