第3章 分类

PS: 个人记录，抄书系列，建议看原书
原书资料：https://github.com/ageron/handson-ml2

3.1 MNIST 数据集

import sklearn
assert sklearn.__version__ >= "0.20"

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784',version=1)
# [1] 默认情况下，Scikit-Learn将下载的数据集缓存在$HOME/scikit_learn_data目录下。

mnist.keys()

dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])

mnist['url']

'https://www.openml.org/d/554'

X, y = mnist['data'], mnist['target']
X.shape,type(X),type(y)

((70000, 784), pandas.core.frame.DataFrame, pandas.core.series.Series)

import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
some_digit =np.array(X[:1])
some_digit_image = some_digit.reshape(28, 28) # np 才有reshape
plt.imshow(some_digit_image, cmap="binary") # cmap=viridis
plt.axis("off") # 清除坐标轴
plt.show() 

​

y[0]

'5'

y = y.astype(np.uint8)

# 划分训练集测试集，人家已经划分好了
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

3.2 训练二元分类器

# 二元分类器，识别 5 和 非5
y_train_5 = (y_train == 5)  # True for all 5s, False for all other digits
y_test_5 = (y_test == 5)
y_train_5

0         True
1        False
2        False
3        False
4        False
         ...  
59995    False
59996    False
59997     True
59998    False
59999    False
Name: class, Length: 60000, dtype: bool

3.2.1 随机梯度下降 SGD

from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)

SGDClassifier(random_state=42)

some_digit.ndim

2

sgd_clf.predict(some_digit) # 要用二维的

array([ True])

3.3 性能测量

python sklearn中KFold与StratifiedKFold

3.3.1 使用交叉验证测量准确率

# 自行实现交叉验证
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3, random_state=42, shuffle = True)
X_train
X_train = np.array(X_train)
for train_index, test_index in skfolds.split(X_train, y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = y_train_5[train_index]

    X_test_fold = X_train[test_index]
    y_test_fold = y_train_5[test_index]

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred)) # prints 0.9502, 0.96565, and 0.96495

0.9669
0.91625
0.96785

# 利用 sklearn 的 cross_val_score
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy") # scoring = 'neg_mean_square_error'得到 -MSE

array([0.95035, 0.96035, 0.9604 ])

cross_val_score的 scoring参数值解析

所有折叠交叉验证的准确率（正确预测的比率）超过93%？看起来挺神奇的，是吗？不过在你开始激动之前，我们来看一个蠢笨的分类器，它将每张图都分类成“非5”：

from sklearn.base import BaseEstimator

class Never5Classifier(BaseEstimator):
    def fit(self, X, y=None):
        return self
    def predict(self, X):
        return np.zeros((len(X), 1), dtype=bool)

never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.91125, 0.90855, 0.90915])

没错，准确率超过90%！这是因为只有大约10%的图片是数字5，所以如果你猜一张图不是5，90%的概率你都是正确的，简直超越了大预言家！这说明准确率通常无法成为分类器的首要性能指标，特别是当你处理有偏数据集时（即某些类比其他类更为频繁）。

3.3.2 混淆矩阵

评估分类器性能的更好方法是混淆矩阵。（对于回归问题可以用损失函数评估）当然，可以通过测试集来进行预测，但是现在先不要动它（测试集最好留到项目的最后，准备启动分类器时再使用）。作为替代，可以使用cross_val_predict（）函数：

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
y_train_pred.size

60000

from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred) # 注意参数顺序

array([[53892,   687],
       [ 1891,  3530]], dtype=int64)

混淆矩阵中的行表示实际类别，列表示预测类别。真负类、假正类、假负类、真正类（TN,FP,FN,TP）

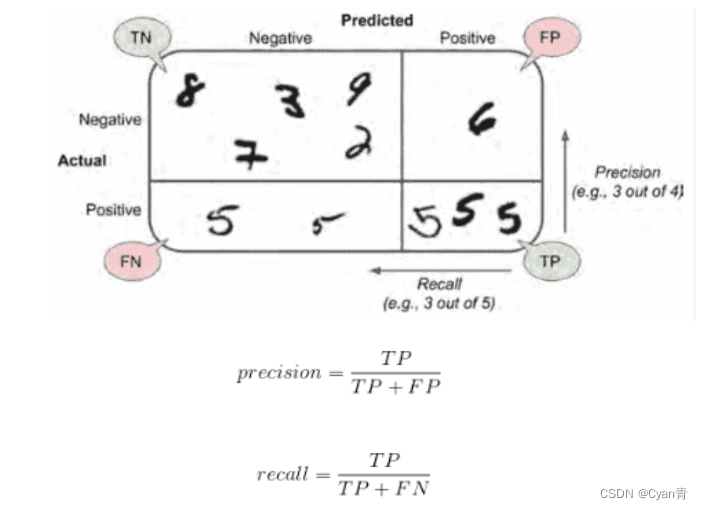
做一个单独的正类预测，并确保它是正确的，就可以得到完美精度（精度=1/1=100%）。但这没什么意义，因为分类器会忽略这个正类实例之外的所有内容。因此，精度通常与另一个指标一起使用，这个指标就是召回率，也称为灵敏度或者真正类率：它是分类器正确检测到的正类实例的比率

3.3.3 精度和召回率

from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred),recall_score(y_train_5, y_train_pred) 

(0.8370879772350012, 0.6511713705958311)

我们可以很方便地将精度和召回率组合成一个单一的指标，称为F1分数。当你需要一个简单的方法来比较两种分类器时，这是个非常不错的指标。

F1分数是精度和召回率的谐波平均值。正常的平均值平等对待所有的值，而谐波平均值会给予低值更高的权重。因此，只有当召回率和精度都很高时，分类器才能得到较高的F1分数。比如(100 + 2) / 2 = 51, 看上去100被拉低了好多

# 调用f1_score()
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)

0.7325171197343846

F1分数对那些具有相近的精度和召回率的分类器更为有利。这不一定能一直符合你的期望：在某些情况下，你更关心的是精度，而另一些情况下，你可能真正关心的是召回率。例如，假设你训练一个分类器来检测儿童可以放心观看的视频，那么你可能更青睐那种拦截了很多好视频（低召回率），但是保留下来的视频都是安全（高精度）的分类器，而不是召回率虽高，但是在产品中可能会出现一些非常糟糕的视频的分类器（这种情况下，你甚至可能会添加一个人工流水线来检查分类器选出来的视频）。反过来说，如果你训练一个分类器通过图像监控来检测小偷：你大概可以接受精度只有30%，但召回率能达到99%（当然，安保人员会收到一些错误的警报，但是几乎所有的窃贼都在劫难逃）。

3.3.4 精度/召回率权衡

对于每个实例，它会基于决策函数计算出一个分值，如果该值大于阈值，则将该实例判为正类，否则便将其判为负类。

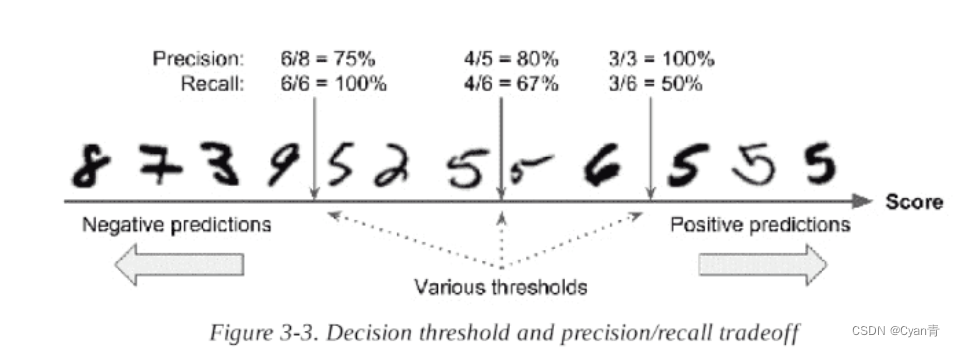
# sklearn 不允许直接设置阈值，但可以获得预测的分数，这样可间接自定义阈值
y_scores = sgd_clf.decision_function(some_digit)
y_scores

array([2164.22030239])

threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

array([ True])

threshold = 8000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

array([False])

可以看出提高阈值，可以降低召回率。那么要如何决定使用什么阈值呢？首先，使用cross_val_predict（）函数获取训练集中所有实例的分数，但是这次需要它返回的是决策分数而不是预测结果：

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                             method="decision_function")
y_scores

array([  1200.93051237, -26883.79202424, -33072.03475406, ...,
        13272.12718981,  -7258.47203373, -16877.50840447])

# 有了这些分数，可以使用precision_recall_curve（）函数
# 来计算所有可能的阈值的精度和召回率：
from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

# 最后，使用Matplotlib绘制精度和召回率相对于阈值的函数图
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.legend()
plt.show()

​

为什么在图3-4中精度曲线比召回率曲线要崎岖一些？要理解原因，可以回头看图3-3，注意，当把阈值从中间箭头往右移动一位数时：精度从4/5（80%）下降到3/4（75%）。另一方面，当阈值上升时，召回率只会下降，这就解释了为什么召回率的曲线看起来很平滑。

总结：分类阈值上升recall必定下降，accuracy 整体上升

假设你决定将精度设为90%。查找图3-4并发现需要设置8000的阈值。更精确地说，你可以搜索到能提供至少90%精度的最低阈值（np.argmax（）会给你最大值的第一个索引，在这种情况下，它表示第一个True值）：

threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
precisions >= 0.90

array([False, False, False, ...,  True,  True,  True])

# 重新计算精确度和召回率
y_train_pred_90 = (y_scores >= threshold_90_precision)
precision_score(y_train_5, y_train_pred_90),recall_score(y_train_5, y_train_pred_90)

(0.9000345901072293, 0.4799852425751706)

现在你有一个90%精度的分类器了（或者足够接近）！如你所见，创建任意一个你想要的精度的分类器是相当容易的事情：只要阈值足够高即可！然而，如果召回率太低，精度再高，其实也不怎么有用！

3.3.5 ROC曲线

还有一种经常与二元分类器一起使用的工具，叫作受试者工作特征曲线（简称ROC）。它与精度/召回率曲线非常相似，但绘制的不是精度和召回率，而是真正类率（召回率的另一名称）和假正类率（FPR）。FPR是被错误分为正类的负类实例比率。它等于1减去真负类率（TNR），后者是被正确分类为负类的负类实例比率，也称为特异度。因此，ROC曲线绘制的是灵敏度（召回率）和（1-特异度）的关系。

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label='ROC_Curve')
    plt.plot([0, 1], [0, 1], 'k--') # Dashed diagonal
plot_roc_curve(fpr, tpr)
plt.legend()
plt.xlabel('fpr')
plt.ylabel('tpr')
plt.show()

​

​

同样这里再次面临一个折中权衡：召回率（TPR）越高，分类器产生的假正类（FPR）就越多。虚线表示纯随机分类器的ROC曲线、一个优秀的分类器应该离这条线越远越好（向左上角）。

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)

0.9604938554008616

有一种比较分类器的方法是测量曲线下面积（AUC）。完美的分类器的ROC AUC等于1，而纯随机分类器的ROC AUC等于0.5。

由于ROC曲线与精度/召回率（PR）曲线非常相似，因此你可能会问如何决定使用哪种曲线。有一个经验法则是，当正类非常少见或者你更关注假正类而不是假负类时，应该选择PR曲线，反之则是ROC曲线。例如，看前面的ROC曲线图（以及ROC AUC分数），你可能会觉得分类器真不错。但这主要是因为跟负类（非5）相比，正类（数字5）的数量真的很少。相比之下，PR曲线清楚地说明分类器还有改进的空间（曲线还可以更接近左上角）。

• c训练一个RandomForestClassifier分类器 比较 它与SGDCLassifier的ROC 和 ROC AUC分数

RandomForestClassifier类没有decision_function（）方法，相反，它有dict_proba（）方法。Scikit-Learn的分类器通常都会有这两种方法中的一种（或两种都有）。dict_proba（）方法会返回一个数组，其中每行代表一个实例，每列代表一个类别，意思是某个给定实例属于某个给定类别的概率（例如，这张图片有70%的可能是数字5）：

from sklearn.ensemble import RandomForestClassifier

forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                    method="predict_proba")
y_scores_forest = y_probas_forest[:, 1]   # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)

plt.plot(fpr, tpr, "b:", label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="lower right")
plt.show()

​

RandomForestClassifier的ROC曲线看起来比SGDClassifier好很多，它离左上角更接近，因此它的ROC AUC分数也高得多：

roc_auc_score(y_train_5, y_scores_forest)

0.9983436731328145

现在你知道如何训练一个二分类器，选择合适的标准，使用交叉验证去评估你的分类器，选择满足你需要的准确率/召回率折衷方案，和比较不同模型的 ROC 曲线和 ROC AUC 数值。现在让我们检测更多的数字，而不仅仅是一个数字 5。

多元分类器

Scikit-Learn可以检测到你尝试使用二元分类算法进行多类分类任务，它会根据情况自动运行OvR或者OvO。我们用sklearn.svm.SVC类来试试SVM分类器（见第5章）：

from sklearn.svm import SVC
svm_clf = SVC()
svm_clf.fit(X_train, y_train) # y_train, not y_train_5
svm_clf.predict(some_digit)

array([5], dtype=uint8)

这段代码使用原始目标类0到9（y_train）在训练集上对SVC进行训练，而不是以“5”和“剩余”作为目标类（y_train_5），然后做出预测（在本例中预测正确）。而在内部，Scikit-Learn实际上训练了45个二元分类器，获得它们对图片的决策分数，然后选择了分数最高的类。要想知道是不是这样，可以调用decision_function（）方法。它会返回10个分数，每个类1个，而不再是每个实例返回1个分数：

some_digit_scores = svm_clf.decision_function(some_digit)
some_digit_scores
# [5] 得分最高

array([[ 1.72501977,  2.72809088,  7.2510018 ,  8.3076379 , -0.31087254,
         9.3132482 ,  1.70975103,  2.76765202,  6.23049537,  4.84771048]])

>>> np.argmax(some_digit_scores)
>>> svm_clf.classes_

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)

svm_clf.classes_[5]

5

# 强制使用 OVR
# 不跑了，太久了
>>> from sklearn.multiclass import OneVsRestClassifier
>>> ovr_clf = OneVsRestClassifier(SVC())
>>> ovr_clf.fit(X_train, y_train)
>>> ovr_clf.predict(some_digit)

# 评估：
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")

# 对数据做标准化后再训练
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")

3.5 误差分析

当然，如果这是一个真正的项目，你将遵循机器学习项目清单中的步骤（见附录B）：探索数据准备的选项，尝试多个模型，列出最佳模型并用GridSearchCV对其超参数进行微调，尽可能自动化，等等。正如你在之前的章节里尝试的那些。在这里，假设你已经找到了一个有潜力的模型，现在你希望找到一些方法对其进一步改进。方法之一就是分析其错误类型。

# 首先看看混淆矩阵。就像之前做的，使用cross_val_predict（）函数进行预测，
# 然后调用confusion_matrix（）函数：
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx

plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show() 

3.6 多标签分类

一个输出表示多个标签

from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)

这段代码会创建一个y_multilabel数组，其中包含两个数字图片的目标标签：第一个表示数字是否是大数（7、8、9），第二个表示是否为奇数。下一行创建一个KNeighborsClassifier实例（它支持多标签分类，不是所有的分类器都支持），然后使用多个目标数组对它进行训练。现在用它做一个预测，注意它输出两个标签：

knn_clf.predict(some_digit)
#数字5确实不大（False），为奇数（True）。

• 评估
  评估多标签分类器的方法很多，如何选择正确的度量指标取决于你的项目。比如方法之一是测量每个标签的F1分数（或者之前讨论过的任何其他二元分类器指标），然后简单地计算平均分数。下面这段代码计算所有标签的平均F1分数：

y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")

这里假设所有的标签都同等重要，但实际可能不是这样。一个简单的办法是给每个标签设置一个等于其自身支持的权重（也就是具有该目标标签的实例的数量）。为此，只需要在上面的代码中设置average="weighted"即可。

3.7 多输出分类

多个标签作为输出

还先从创建训练集和测试集开始，使用NumPy的randint（）函数为MNIST图片的像素强度增加噪声。目标是将图片还原为原始图片：

图片由像素点构成，每个像素点看作一个标签

noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test

some_index = 0
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
save_fig("noisy_digit_example_plot")
plt.show()

# 左边是有噪声的输入图片，右边是干净的目标图片。现在通过训练分类器，清洗这张图片：
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit) 

看起来离目标够接近了。分类器之旅到此结束。希望现在你掌握了如何为分类任务选择好的指标，如何选择适当的精度/召回率权衡，如何比较多个分类器，以及更为概括地说，如何为各种任务构建卓越的分类系统。