通透理解FlashAttention与FlashAttention2：大模型更长上下文的关键

前言

本文最初和第一代ChatGLM-6B的内容汇总在一块，但为了阐述清楚FlashAttention、FlashAttention2等相关的原理，导致之前那篇文章越写越长，故特把FlashAttention相关的内容独立抽取出来成本文

且本文会和本博客内其他大模型相关的文章一样，极其注重可读性，比如为了不断提高可读性，本文近期会不断反复修改，细抠标题的层级、措辞，甚至排版、标点符号，如果不通俗易懂，宁愿不写

如果你对某一节的某一个内容或某一个公式没看明白，请随时于本文评论下留言，一定及时修订以让君明白

第一部分理解FlashAttention所必须的背景知识

FlashAttention是斯坦福联合纽约州立大学在22年6月份提出的一种具有 IO 感知，且兼具快速、内存高效的新型注意力算法「对应论文为：FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness，这是其GitHub地址，这是其解读之一，该解读也是本第二部分的重要参考之一」

它要解决一个什么样的问题呢？

首先，GPT3、LLaMA、ChatGLM、BLOOM等大语言模型输入输出的最大序列长度只有2048或4096，扩展到更长序列的难度在哪里呢？本质原因是，transformer模型的计算复杂度和空间复杂度都是 $O(N^2)$ 的，其中 $N$ 为序列长度
如此，FlashAttention提出了一种加速计算、节省显存和IO感知的精确注意力，可以有效地缓解上述问题

Meta推出的开源大模型LLaMA，阿联酋推出的开源大模型Falcon都使用了Flash Attention来加速计算和节省显存。目前，Flash Attention已经集成到了pytorch2.0中，另外triton、xformer等开源框架也进行了整合实现

1.1 Transformer计算复杂度——Self-Attention层与MLP层

当输入批次大小为 $b$ ，序列长度为 $N$ 时，
$l$ 层transformer模型的计算量为 $l *\left(24 b N h^{2}+4 b N^{2} h\right)$ ， $h$ 是隐藏层维度通常等于词向量维度，可能不少同学都会疑问这个计算量是怎么一步一步计算得来的，下面详细拆解下这个计算过程

首先，我们知道，transformer模型由 $l$ 个相同的层组成，每个层分为两部分：self-attention块和MLP块

1.1.1 Self-Attention层的计算复杂度

self-attention层的模型参数有两部分，一部分是 $Q$ 、 $K$ 、 $V$ 的权重矩阵 $W_Q$ 、 $W_K$ 、 $W_V$ 和偏置，另一部分是输出权重矩阵 $W_O$ 和偏置，最终为： $8bNh^2 + 4bN^2h$

具体怎么计算得来的呢？

第一步是计算 $Q$ 、 $K$ 、 $V$
即 $Q=x W_{Q}, K=x W_{K}, V=x W_{V}$
该矩阵乘法的输入和输出形状为 $[b, N, h] \times[h, h] \rightarrow[b, N, h]$
计算量为： $3 * 2 b N h^{2}=6 b N h^{2}$ 
计算 $Q K^T$
该部分的输入和输出形状为
$\left[b, h e a d \_n u m, l, p e r \_h e a d \_h i d d e n \_s i z e\right]$ $\times$ $\left[b, h e a d \_n u m, p e r \_h e a d \_h i d d e n \_s i z e\right. , N] \rightarrow\left[b, h e a d \_n u m, N, l\right]$
计算量为： $2bN^2h$ 
计算在 $V$ 上的加权 $score \cdot V$
该部分矩阵乘法的输入和输出形状为
$\left[b, h e a d \_n u m, l, l\right] \times\left[b, h e a d \_n u m, l, p e r \_h e a d \_h i d d e n \_s i z e\right]$ $\rightarrow\left[b, h e a d \_n u m, N, p e r \_h e a d \_h i d d e n \_s i z e\right]$
计算量为： $2bN^2h$ 
attention后的线性映射，矩阵乘法的输入和输出形状为 $[b, N, h] \times[h, h] \rightarrow[b, N, h]$
计算量为 $2bNh^2$ 

最终自注意力层的输出结果为
$x_{o u t}=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{h}}\right) \cdot V \cdot W_{o}+x$

1.1.2 MLP层的计算复杂度

MLP块由2个线性层组成，最终是 $16bNh^2$

怎么计算得来的呢？

一般地，第一个线性层是，第二个线性层再将维度从 $4h$ 映射到 $h$
$x=f_{\text {gelu }}\left(x_{\text {out }} W_{1}\right) W_{2}+x_{\text {out }}$

第一个线性层的权重矩阵 $W_1$ 的形状为 $[h,4h]$ ，相当于先将维度从 $h$ 映射到 $4h$ ，矩阵乘法的输入和输出形状为 $[b, N, h] \times[h, 4 h] \rightarrow[b, N, 4 h]$ ，计算量为 $8bNh^2$ 
第二个线性层的权重矩阵 $W_2$ 的形状为 $[4h,h]$ ，相当于再将维度从 $4h$ 映射到 $h$ ，矩阵乘法的输入和输出形状为 $[b, N, 4 h] \times[4 h, h] \rightarrow[b, N, h]$ ，计算量为 $8bNh^2$ 
将上述所有表粗所示的计算量相加，得到每个transformer层的计算量大约为
$24 b N h^{2}+4 b N^{2} h$
此外，另一个计算量的大头是logits的计算(毕竟词嵌入矩阵的参数量也较多)，将隐藏向量映射为词表大小，说白了，词向量维度通常等于隐藏层维度 $h$ ，词嵌入矩阵的参数量为 $Vh$ ，最后的输出层的权重矩阵通常与词嵌入矩阵是参数共享的「解释一下，如七月杜老师所说，这个是transformer中一个重要的点，参数共享可以减小参数量，词嵌入矩阵是[vocab_size，hidden_size]，输出层矩阵是 [hidden_size，vocab_size]，是可以共享的」
其矩阵乘法的输入和输出形状为 $[b, N, h] \times[h, V] \rightarrow[b, N, V]$ ，计算量为 $2bNhV$
因此，对于一个 $l$ 层的transformer模型，输入数据形状为 $[b,N]$ 的情况下，一次训练迭代的计算量为
$l *\left(24 b N h^{2}+4 b N^{2} h\right)+2 b N h V$

1.2 Transformer的空间复杂度——Self-Attention层与MLP层

中间激活的显存大小为 $l *\left(34 b N h+5 b N^{2} a\right)$ ，其中 $a$ 为注意力头数

大模型在训练过程中通常采用混合精度训练，中间激活值一般是float16或者bfloat16数据类型的。在分析中间激活的显存占用时，假设中间激活值是以float16或bfloat16数据格式来保存的，每个元素占了2个bytes。唯一例外的是，dropout操作的mask矩阵，每个元素只占1个bytes。在下面的分析中，单位是bytes，而不是元素个数。

每个transformer层包含了一个self-attention块和MLP块，并分别对应了一个layer normalization连接。

1.2.1 Self-Attention块的中间激活

self-attention块的计算公式如下：

$Q=x W_{Q}, K=x W_{K}, V=x W_{V}$
$x_{o u t}=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{h}}\right) \cdot V \cdot W_{o}+x$

最终，self-attention块的中间激活占用显存大小为： $11 b N h+5 b N^{2} a$

具体怎么计算得来的呢？

对于 $Q,K,V$ ，需要保存它们共同的输入 $x$ ，这就是中间激活。输入 $x$ 的形状为 $[b, N, h]$ ，元素个数为 $bNh$ ，占用显存大小为 $2 * b N h=2 b N h$
对于 $Q K^{T}$ 矩阵乘法，需要保存中间激活 $Q,K$ ，两个张量的形状都是 $[b,s,h]$ ，占用显存大小合计为 $2 * 2 * b N h=4 b N h$
对于 $\text { softmax () }$ 函数，需要保存函数的输入 $Q K^{T}$ ，占用显存大小为 $2 b N^{2} a$ ，这里的 $a$ 表示注意力头数
$\text { score }=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right)$

其中
$Q$ 的形状为： $\left[b, h e a d \_n u m, N, p e r \_h e a d \_h i d d e n \_s i z e\right]$
$K^{T}$ 的形状为： $\left[b, h e a d \_n u m, p e r \_h e a d \_h i d d e n \_s i z e, N\right]$
$Q K^{T}$ 的形状为： $\left[b, h e a d \_n u m, N, N\right]$ ，元素个数为 $b N^{2} a$ ，占用显存大小为 $2 b N^{2} a$
计算完 $\text { softmax () }$ 函数后，会进行dropout操作。需要保存一个mask矩阵，mask矩阵的形状与 $Q K^{T}$ 相同，占用显存大小为 $b N^{2} a$
计算在 $V$ 上的attention，即 $\text { score } \cdot V$ ，需要保存 $\text { score }$ ，大小为 $2 b N^{2} a$ ；以及 $V$ ，大小为 $2 b N h$ ，二者占用显存大小合计为 $2 b N^{2} a+2 b N h$
计算输出映射以及一个dropout操作。输入映射需要保存其输入，大小为 $2 b s h$ ；dropout需要保存mask矩阵，大小为 $\text { bsh }$ ，二者占用显存大小合计为 $3 b N h$

因此，将上述中间激活相加得到，self-attention块的中间激活占用显存大小为 $11 b N h+5 b N^{2} a$

1.2.2 MLP块的中间激活

MLP块的计算公式如下： $x=f_{\text {gelu }}\left(x_{\text {out }} W_{1}\right) W_{2}+x_{\text {out }}$ ，最终对于MLP块，需要保存的中间激活值为 $19 b N h$

具体怎么计算得来的呢？

第一个线性层需要保存其输入，占用显存大小为 $2 b N h$
激活函数需要保存其输入，占用显存大小为 $8 b N h$
第二个线性层需要保存其输入，占用显存大小为 $8 b N h$
最后有一个dropout操作，需要保存mask矩阵，占用显存大小为 $\text { bNh }$

1.2.3 两个layer norm需要保存的中间激活

另外，self-attention块和MLP块分别对应了一个layer normalization。每个layer norm需要保存其输入，大小为 $2bNh$ ，2个layer norm需要保存的中间激活为 $4bNh$

综上，每个transformer层需要保存的中间激活占用显存大小为 $34 b N h+5 b N^{2} a$

对于 $l$ 层transformer模型，还有embedding层、最后的输出层。embedding层不需要中间激活。总的而言，当隐藏维度 $h$ 比较大，层数 $l$ 较深时，这部分的中间激活是很少的，可以忽略

因此，对于 $l$ 层transformer模型，中间激活占用的显存大小可以近似为 $\left(34 b N h+5 b N^{2} a\right) * l$ 「更多分析见此文《分析transformer模型的参数量、计算量、中间激活、KV cache》」

通过上面两小节的内容，可以看到，transformer模型的计算量和储存复杂度随着序列长度 $N$ 呈二次方增长。这限制了大语言模型的最大序列长度 $N$ 的大小

其次，GPT4将最大序列长度 $N$ 扩大到了32K，Claude更是将最大序列长度 $N$ 扩大到了100K，这些工作一定采用了一些优化方法来降低原生transformer的复杂度，那具体怎么优化呢？
我们知道，每个transformer层分为两部分：self-attention块和MLP块，但上面计算量中的 $4bN^2h$ 项和中间激活中的 $5bN^2a$ 项都是self-attention块产生的，与MLP块无关

1.3 如何改进safe softmax已提升计算速度

对于safe softmax而言

考虑到向量 $\left[x_{1}, x_{2}, \cdots, x_{d}\right]$ ，原生softmax的计算过程如下：
$\operatorname{softmax}\left(x_{i}\right)=\frac{e^{x_{i}}}{\sum_{j=1}^{d} e^{x_{j}}}$
在实际硬件中，浮点数表示的范围是有限的
对于float32和bfloat16来说，当 $x \geq 89$ 时， $e^x$ 就会变成inf，发生数据上溢的问题
故为了避免发生数值溢出的问题，保证数值稳定性，计算时通常会“减去最大值”，称为“safe softmax”

即现在所有的深度学习框架中都采用了“safe softmax”这种计算方式
$m=\max _{i}\left(x_{i}\right) ; \quad \operatorname{softmax}\left(x_{i}\right)=\frac{e^{x_{i}-m}}{\sum_{j=1}^{d} e^{x_{j}-m}}$
在训练语言模型时，通常会采用交叉熵损失函数。交叉熵损失函数等价于先执行log_softmax函数，再计算负对数似然函数
且在计算log_softmax时，同样会执行“减去最大值”，这不仅可以避免数值溢出，提高数值稳定性，还可以加快计算速度
$\log \left(\operatorname{softmax}\left(x_{i}\right)\right)=\log \left(\frac{e^{x_{i}-m}}{\sum_{j=1}^{d} e^{x_{j}-m}}\right)=x_{i}-m-\log \left(\sum_{j=1}^{d} e^{x_{j}-m}\right)$

1.4 GPU的内存分析图：降低注意力复杂度只是一方面，计算的更大瓶颈是显存访问

通过上文可知

transformer的核心组件self-attention块的计算复杂度和空间复杂度是序列长度 $N$ 的二次方
但对于self-attention块，除了大矩阵乘法是计算受限的，其他操作(计算softmax、dropout、mask）都是内存受限的
尽管已经有许多近似注意力的方法尝试减少attention的计算和内存要求。例如，稀疏近似和低秩近似的方法，将计算复杂度降低到了序列长度的线性或亚线性
但这些近似注意力方法方法并没有得到广泛应用。因为这些方法过于关注FLOPs(浮点数计算次数)的减少，而忽略了IO读写的内存访问开销，导致这并没有效减少运行时间(wall-clock time)
总之，在现代GPU中，计算速度已经远超过了显存访问速度，transformer中的大部分计算操作的瓶颈是显存访问。对于显存受限的操作，IO感知是非常重要的，因为显存读写占用了大部分的运行时间
而Flash Attention则是IO感知的，通过减少内存访问，来计算精确注意力，从而减少运行时间，实现计算加速

GPU的内存由多个不同大小和不同读写速度的内存组成。内存越小，读写速度越快。对于A100-40GB来说，内存分级图如下所示

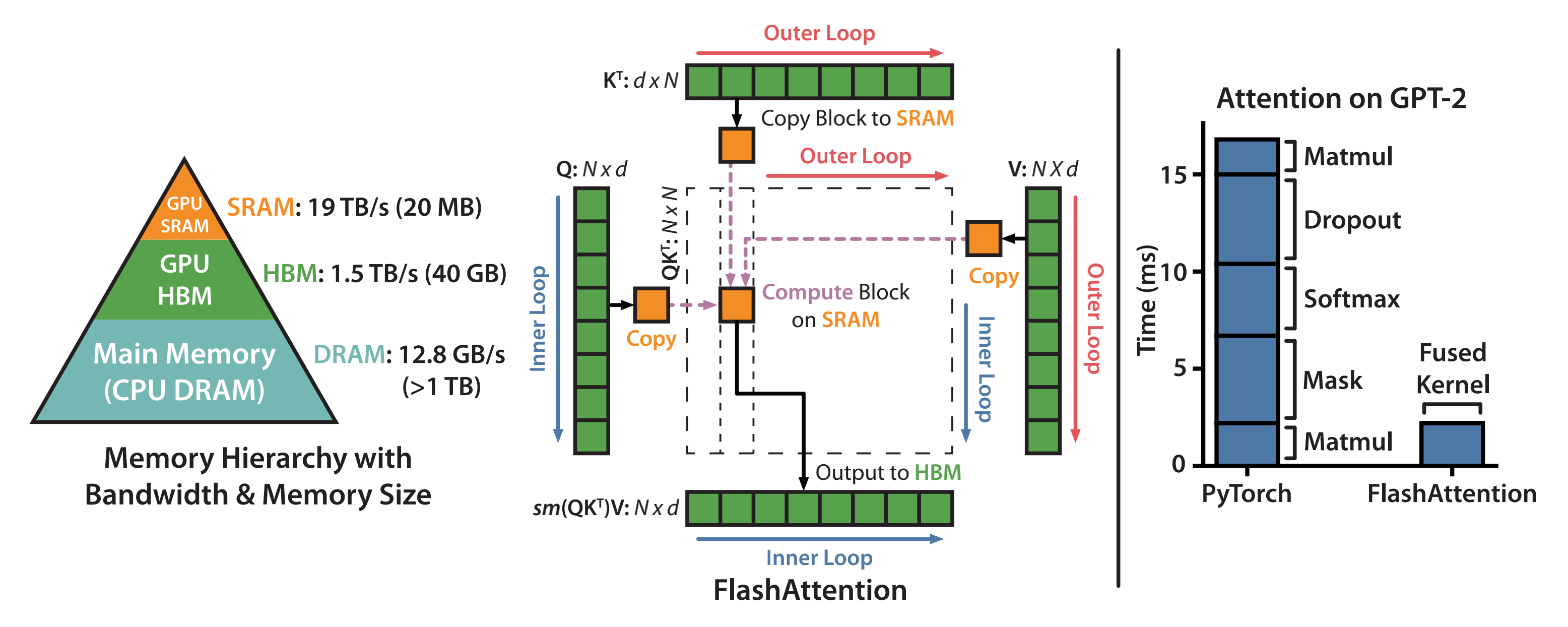
SRAM内存分布在108个流式多处理器上，每个处理器的大小为192K。合计为 $192 * 108 K B=20,736 K M=20 M B$
高带宽内存HBM（High Bandwidth Memory），也就是我们常说的显存，大小为40GB。SRAM的读写速度为19TB/s，而HBM的读写速度只有1.5TB/s，不到SRAM的1/10

所以，上面讲到计算注意力的主要瓶颈是显存访问，因此减少对HBM的读写次数，有效利用更高速的SRAM来进行计算是非常重要的，而GPU有大量的线程来执行某个操作，称为kernel。GPU执行操作的典型方式分为三步：

每个kernel将输入数据从低速的HBM中加载到高速的SRAM中
在SRAM中，进行计算
计算完毕后，将计算结果从SRAM中写入到HBM中

而对于性能受限于内存带宽的操作，进行加速的常用方式就是kernel融合。kernel融合的基本思想是：避免反复执行“从HBM中读取输入数据，SRAM执行计算，最后将计算结果写入到HBM中”，将多个操作融合成一个操作，减少读写HBM的次数(需要注意的是，模型训练通常会影响到算子融合的效果，因为为了后向传递计算梯度，通常需要将某些中间结果写入到HBM中)

第二部分 FlashAttention：减少内存访问提升计算速度——更长上下文的关键

2.1 前向传递：Standard Attention/Memory-efficient Attention/Flash Attention

2.2.1 Standard Attention

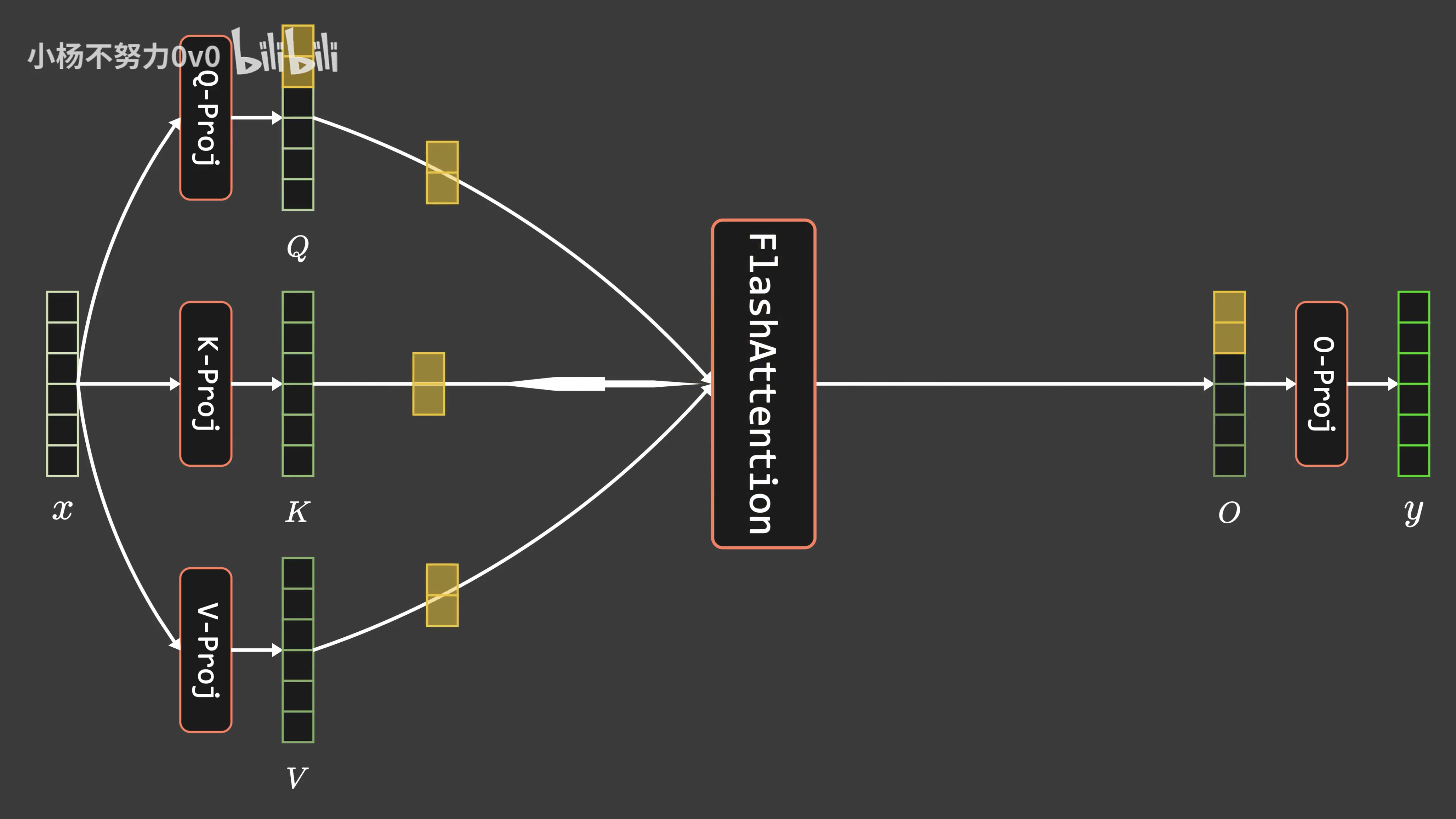
首先，transformer中注意力机制的计算过程为：
$\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{\top}}{\sqrt{d}}\right) V$
其中， $Q, K, V \in R^{N \times d}$ ，其中 $N$ 是序列长度， $d$ 是每个注意力头的维度，输出可以记为 $O \in R^{N \times d}$
上面的式子可以拆解为：
$S=Q K^{\top} \in R^{N \times N}, P=\operatorname{softmax}(S) \in R^{N \times N}, O=P V \in R^{N \times d}$
在标准注意力实现中， $S, P \in R^{N \times N}$ 都要写回到HBM中，占用了 $O\left(N^{2}\right)$ 的内存，通常 $N \gg d$
例如，对于GPT2， $N = 1024$ ， $d = 64$ ；对于GPT3， $N = 1028$ ， $d = 128$

总之，注意力矩阵 $P, S$ 需要的内存 $O\left(N^{2}\right)$ 远大于 $Q, K, V, O$ 所需要的内存 $O(N d)$
相当于，self-attention中，大部分操作都是内存受限的逐点运算，例如，对 $S$ 的mask操作、 $S$ 的softmax操作、对 $P$ 的dropout操作，这些逐点操作的性能是受限于内存带宽的，会减慢运行时间
下图展示了标准注意力的实现过程

标准注意力实现存在两个问题：
1. 显存占用多，过程中由于实例化了完整的注意力矩阵 $P, S \in R^{N \times N}$ ，导致了 $O\left(N^{2}\right)$ 的内存要求
2. HBM读写次数多，减慢了运行时间(wall- clock time)

接下来2.2.2节中的Memory-efficient Attention、2.2.3节中的Flash Attention，便是要分别解决上述这两个问题

2.2.2 Memory-efficient Attention：把显存复杂度从平方降低到线性，但HBM访问次数仍是平方

在注意力计算过程中，节省显存的主要挑战是softmax与 $K,V$ 的列是耦合的。其方法是单独计算softmax的归一化因子，来实现解耦

为了简化分析，忽略计算softmax时“减去最大值”的步骤
记 $Q$ 的第 $i$ 列为 $q_{i} \in R^{d}$ ， $K$ 的第 $j$ 列为 $K_{j} \in R^{d}$ ，有 $S_{i j}=q_{i}^{\top} k_{j} \in R$
定义softmax的归一化因子为：
$L_{i}=\sum_{j} e^{q_{i}^{\top} k_{j}} \in R$
记 $v_{j} \in R^{d}$ 为 $V$ 的第 $j$ 个列向量，则输出 $O$ 的第 $i$ 个列向量 $o_i$ 为：
$o_{i}=P_{i:} V=\sum_{j} P_{i j} v_{j}=\sum_{j} \frac{e^{q_{i}^{\top} k_{j}}}{L_{i}} v_{j}$
在计算得到归一化因子 $L_i$ 后，就可以通过反复累加 $\frac{e^{q_{i}^{\top} k_{j}}}{L_{i}} v_{j}$ 来得到 $o_i$

如此，节省内存(memory-efficient)的注意力机制，改变了计算顺序，相比于Standard Attention，节省显存的注意力机制将显存复杂度从 $O(N^2)$ 降低到了 $O(N)$

这种方法在《Online normalizer calculation for softmax》和《Self-attention Does Not Need $O\left(n^{2}\right)$ Memory》中已经使用过，称其为“lazy softmax”，这种方法避免了实例化完整的注意力矩阵 $S,P$ ，从而达到了节省显存的目的。然而HBM访问次数仍然是 $O(N^2)$ 的，因此运行时间并没有减少

2.2.3 Flash Attention：降低HBM读写次数，避免频繁地从HBM中读写数据

如上文说过的

在标准注意力实现中，注意力的性能主要受限于内存带宽，是内存受限的。频繁地从HBM中读写 $N \times N$ 的矩阵是影响性能的主要瓶颈
稀疏近似和低秩近似等近似注意力方法虽然减少了计算量FLOPs，但对于内存受限的操作，运行时间的瓶颈是从HBM中读写数据的耗时，减少计算量并不能有效地减少运行时间(wall-clock time)
针对内存受限的标准注意力，Flash Attention是IO感知的，目标是避免频繁地从HBM中读写数据

2.3.3.1 tiling：分块计算注意力

从GPU显存分级来看，SRAM的读写速度比HBM高一个数量级，但内存大小要小很多

通过kernel融合的方式，将多个操作融合为一个操作，利用高速的SRAM进行计算，可以减少读写HBM的次数，从而有效减少内存受限操作的运行时间。但SRAM的内存大小有限，不可能一次性计算完整的注意力，因此必须进行分块计算，使得分块计算需要的内存不超过SRAM的大小
相当于，内存受限 --> 减少HBM读写次数 --> kernel融合 --> 满足SRAM的内存大小 --> 分块计算。因此分块大小block_size不能太大，否则会导致OOM
而分块计算的难点是什么呢？
注意力机制的计算过程是“矩阵乘法 --> scale --> mask --> softmax --> dropout --> 矩阵乘法”，矩阵乘法和逐点操作(scale，mask，dropout)的分块计算是容易实现的，难点在于softmax的分块计算。由于计算softmax的归一化因子(分母)时，需要获取到完整的输入数据，进行分块计算的难度比较大

tiling的主要思想是分块计算注意力。分块计算的难点在于softmax的分块计算，softmax与 $K$ 的列是耦合的，通过引入了两个额外的统计量 $m(x),l(x)$ 来进行解耦，实现了分块计算。为了保证数值稳定性，对于 $x \in R^{B}$ ，执行“减去最大值”的safe softmax的计算过程如下：

$m(x):=\max _{i} \quad x_{i}$

$\quad f(x):=\left[\begin{array}{lll} e^{x_{1}-m(x)} & \ldots & e^{x_{B}-m(x)} \end{array}\right]$

$\quad \ell(x):=\sum_{i} f(x)_{i}$

$\quad \operatorname{softmax}(x):=\frac{f(x)}{\ell(x)}$

对于两个向量 $x^{(1)}, x^{(2)} \in R^{B}$ ，解耦拼接向量 $x=\left[x^{(1)}, x^{(2)}\right] \in R^{2 B}$ 的softmax计算：

$m(x)=m\left(\left[x^{(1)} x^{(2)}\right]\right)=\max \left(m\left(x^{(1)}\right), m\left(x^{(2)}\right)\right)$

$\quad f(x)=\left[e^{m\left(x^{(1)}\right)-m(x)} f\left(x^{(1)}\right) \quad e^{m\left(x^{(2)}\right)-m(x)} f\left(x^{(2)}\right)\right]$

$\ell(x)=\ell\left(\left[x^{(1)} x^{(2)}\right]\right)=e^{m\left(x^{(1)}\right)-m(x)} \ell\left(x^{(1)}\right)+e^{m\left(x^{(2)}\right)-m(x)} \ell\left(x^{(2)}\right)$

$\quad \operatorname{softmax}(x)=\frac{f(x)}{\ell(x)}$

通过保持两个额外的统计量 $m(x),l(x)$ ，可以实现softmax的分块计算。需要注意的是，可以利用GPU多线程同时并行计算多个block的softmax。为了充分利用硬件性能，多个block的计算不是串行（sequential）的，而是并行的。

下面通过例子说明如何分块计算softmax。对向量 [1,2,3,4] 计算softmax，分成两块 [1,2] 和 [3,4] 进行计算。计算block 1：

$\begin{array}{l} m_{1}=\max ([1,2])=2\\ \begin{array}{c} f_{1}=\left[e^{1-2}, e^{2-2}\right]=\left[e^{-1}, e^{0}\right] \\ l_{1}=\sum f_{1}=e^{-1}+e^{0} \\ o_{1}=\frac{f_{1}}{l_{1}}=\frac{\left[e^{-1}, e^{0}\right]}{e^{-1}+e^{0}} \end{array} \end{array}$

计算block 2:

$\begin{array}{l} m_{2}=\max ([3,4])=4\\ \begin{array}{c} f_{2}=\left[e^{3-4}, e^{4-4}\right]=\left[e^{-1}, e^{0}\right] \\ l_{2}=\sum f_{2}=e^{-1}+e^{0} \\ o_{2}=\frac{f_{2}}{l_{2}}=\frac{\left[e^{-1}, e^{0}\right]}{e^{-1}+e^{0}} \end{array} \end{array}$

合并得到完整的softmax结果：

$\begin{array}{l} m=\max \left(m_{1}, m_{2}\right)=4\\ f=\left[e^{m_{1}-m} f_{1}, e^{m_{2}-m} f_{2}\right]=\left[e^{-3}, e^{-2}, e^{-1}, e^{0}\right]\\ l=e^{m_{1}-m} l_{1}+e^{m_{2}-m} l_{2}=e^{-3}+e^{-2}+e^{-1}+e^{0}\\ o=\frac{f}{l}=\frac{\left[e^{-3}, e^{-2}, e^{-1}, e^{0}\right]}{e^{-3}+e^{-2}+e^{-1}+e^{0}} \end{array}$

在忽略mask和dropout的情况下，简化分析，Flash Attention算法的前向计算过程如下所示。从下图可以看到，该算法在 $K,V$ 的维度上做外循环，在 $Q$ 的维度上做内循环。而在triton的代码实现中，则采用了在 $Q$ 的维度上做外循环，在 $K,V$ 的维度上做内循环

2.3.3.2 重计算

上文讲到，模型训练会影响kernel融合的效果，为了后向传递计算梯度，前向计算时通常需要将某些中间结果写回到HBM中，这会产生额外的HBM读写次数，减慢运行时间。因此，Flash Attention没有为后向传递保存很大的中间结果矩阵。

在标准注意力实现中，后向传递计算 $Q,K,V$ 的梯度时，需要用到 $N \times N$ 的中间矩阵 $S,P$ ，但这两个矩阵并没有保存下来。这里的技巧是重计算，保存了两个统计量 $m(x),l(x)$ ，后向传递时在高速的SRAM上快速地重新计算Attention，通过分块的方式重新计算注意力矩阵 $S,P$ 。相比于标准注意力中，从HBM中读取很大的中间注意力矩阵的方法，重计算的方法要快得多。

总的来说，Flash Attention通过调整注意力的计算顺序，引入两个额外的统计量进行分块计算，避免了实例化完整的 $N \times N$ 的注意力矩阵 $S,P$ ，将显存复杂度从 $O\left(N^{2}\right)$ 降低到了 $O\left(N\right)$ 。另外，对于内存受限的标准注意力，Flash Attention通过kernel融合和分块计算，大量减少了HBM访问次数，尽管由于后向传递中的重计算增加了额外的计算量FLOPs，减少了运行时间，计算速度更快（GPT2的7.6倍）。

2.3.3.3 kernel融合

为了简化分析，上文介绍注意力时忽略了mask和dropout操作。下面详细介绍Flash Attention前向传递的细节。给定输入 $Q, K, V \in R^{N \times d}$ ，计算得到注意力输出 $O^{N \times d}$

$\begin{array}{c} S=\tau Q K^{\top} \in R^{N \times N} \\ S^{\text {masked }}=M A S K(S) \in R^{N \times N} \\ P=\operatorname{softmax}\left(S^{\text {masked }}\right) \in R^{N \times N} \\ P^{\text {dropped }}=\operatorname{dropout}\left(P, p_{d r o p}\right) \in R^{N \times N} \\ O=P^{\text {dropped }} V \in R^{N \times d} \end{array}$

其中， $\tau$ 是softmax的缩放因子，典型的比如 $\frac{1}{\sqrt{d_{k}}}$ 。MASK操作将输入中的某些元素置为 −∞ ，计算softmax后就变成了0，其他元素保持不变；causal-lm结构和prefix-lm结构的主要差别就是MASK矩阵不同。 $\text { dropout }(x, p)$ 逐点作用在 $x$ 的每个元素上，以 $p$ 的概率将该元素置为0，以 $1-p$ 的概率将元素置为 $\frac{x}{1-p}$

tiling分块计算使得我们可以用一个CUDA kernel来执行注意力的所有操作。从HBM中加载输入数据，在SRAM中执行所有的计算操作(矩阵乘法、mask、softmax、dropout、矩阵乘法)，再将计算结果写回到HBM中。通过kernel融合将多个操作融合为一个操作，避免了反复地从HBM中读写数据