📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 二叉树的最大深度
- 二叉树的最小深度
- 完全二叉树的节点个数
- 总结:
先看第一题,求二叉树的最大深度
二叉树的最大深度
104. 二叉树的最大深度 - 力扣(LeetCode)
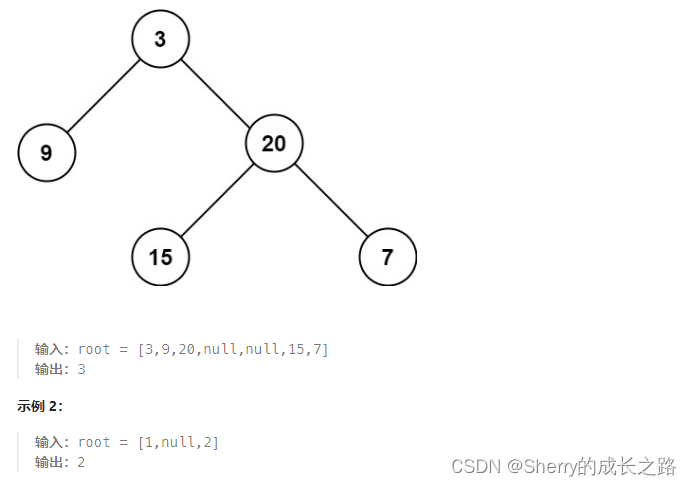
这道题的思路主要有两种,第一种是正常求解二叉树的最大深度,即从上至下搜索,二叉树最大深度的定义是从根节点到叶子节点的最远距离为二叉树的最大深度。我们可以按照前序遍历的方法向下遍历,依次统计出到叶子结点的距离,取最大值即可。
第二种思路是由于二叉树的最大高度就是二叉树的最大深度,所以可以采用求二叉树最大高度的方法求解出本题,高度是逐渐变小的从根节点到叶子节点,这是它和直接求深度的本质区别,这个时候我们可以以后序遍历的方法来从上到下求取最大高度,完成求解。
先给出正常逻辑求深度的代码
class Solution {
public:
int result=0;
void dfs(TreeNode*root,int deepth){
result=result>deepth?result:deepth;
if(root->left)dfs(root->left,deepth+1);
if(root->right)dfs(root->right,deepth+1);
}
int maxDepth(TreeNode* root) {
if(root==NULL)return 0;
dfs(root,1);
return result;
}
};
下面的是以求高度的思路写出的代码
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root==nullptr)
{
return 0;
}
int leftval=maxDepth(root->left);
int rightval=maxDepth(root->right);
int max1=1+max(leftval,rightval);
return max1;
}
};
两种思路中我更偏向于按照深度的思路,这种思路我觉得更利于理解。
二叉树的最小深度
111. 二叉树的最小深度 - 力扣(LeetCode)
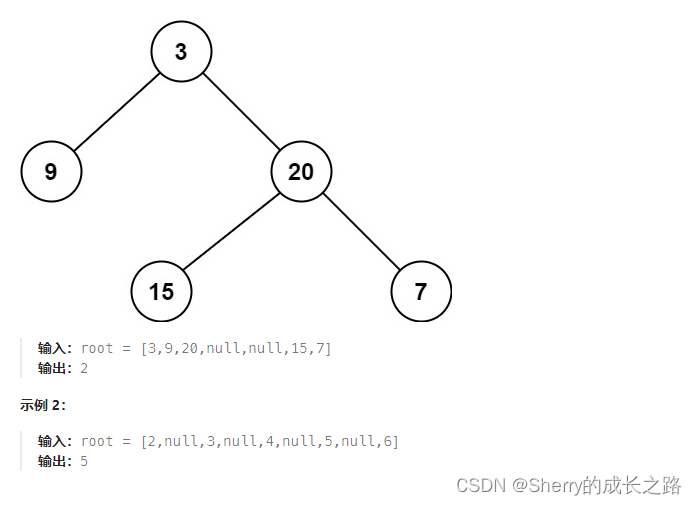
这道题是求解二叉树的最小深度,如果按照直接求深度的思想写代码思路相差的并不多。只有一点需要注意,并不是直接取deepth和result中的最小值,因为那样直接去取最小值,会出现当根节点一开始左子树或右子树有一个没有的情况时,会直接使result附上结果为1的答案,但是实际上这与二叉树的深度定义本身是不相符合的,深度的定义是根节点到叶子结点的距离,所以一定要遍历到叶子节点时才能算是一个答案,具体代码看下面。
class Solution {
public:
int result=INT_MAX;
void dfs(TreeNode* root,int deepth)
{
if(root->left==nullptr&&root->right==nullptr)
{
result=result<deepth?result:deepth;
}
if(root->left)
{
dfs(root->left,deepth+1);
}
if(root->right)
{
dfs(root->right,deepth+1);
}
}
int minDepth(TreeNode* root) {
if(root==nullptr)
{
return 0;
}
dfs(root,1);
return result;
}
};
上面的代码已经很清晰的写出了,求解最小深度的代码,当该节点的左右节点都为空时候,那么该节点才是叶子节点,这时候我们再收获答案,进行比较。第二种思路在这里就不给出了,和这种思路差不太多,但是本人认为使用高度来求深度应用在这道题中稍显麻烦了一些。
完全二叉树的节点个数
222. 完全二叉树的节点个数 - 力扣(LeetCode)
这道题也分成两种大致的思路,一种是按照正常思路解,即不管他是什么类型的二叉树,直接将所有节点全遍历一次,记录下一共遍历了几个节点,后返回答案,这样的思路无论是什么二叉树都能遍历出来,属于暴力解法。这里不给出代码。
第二种思路就是按照满二叉树的解法,满二叉树一定是完全二叉树,由于完全二叉树中一定会有某子树是完全二叉树,我们按照这样的性质来遍历,判断从根节点开始的各个子树是否满足满二叉树的特点来求解,这样的好处是可以减少遍历一部分的中间节点,但是值得注意的是,时间复杂度貌似和暴力求解差不多都是On。
class Solution {
public:
int countNodes(TreeNode* root) {
if(root==nullptr)
{
return 0;
}
TreeNode* left=root->left;
int leftval=0,rightval=0;
TreeNode* right=root->right;
while(left)
{
left=left->left;
leftval++;
}
while(right)
{
right=right->right;
rightval++;
}
if(leftval==rightval)
{
return (2<<leftval)-1;
}
return countNodes(root->left)+countNodes(root->right)+1;
}
}
代码绝大部分是结束判断语句,判断从某节点起始,它的子树是否为完全二叉树,因为如果是的话从该节点的两侧开始遍历如果节点数目相等,那么肯定就是完全二叉树,按照这样的思路,即可完成判断。判断成功了,返回的是当前完全二叉树共多少节点。这个代码不需要担心如果有单独节点出现,因为单独节点没有左右子树,也可以看作为完全二叉树!
总结:
今天我们完成了二叉树的最大深度、二叉树的最小深度、完全二叉树的节点个数三道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~