本文深入探讨了期望最大化（EM）算法的原理、数学基础和应用。通过详尽的定义和具体例子，文章阐释了EM算法在高斯混合模型（GMM）中的应用，并通过Python和PyTorch代码实现进行了实战演示。

关注TechLead，分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验，同济本复旦硕，复旦机器人智能实验室成员，阿里云认证的资深架构师，项目管理专业人士，上亿营收AI产品研发负责人。

一、引言

期望最大化算法（Expectation-Maximization Algorithm，简称EM算法）是一种迭代优化算法，主要用于估计含有隐变量（latent variables）的概率模型参数。它在机器学习和统计学中有着广泛的应用，包括但不限于高斯混合模型（Gaussian Mixture Model, GMM）、隐马尔可夫模型（Hidden Markov Model, HMM）以及各种聚类和分类问题。

概率模型与隐变量

概率模型是一种用数学表示的数据生成过程。在统计学和机器学习中，一个概率模型通常用来描述观测数据（observable data）和潜在结构（latent structure）之间的关系。

• 例子：假设我们有一个数据集，包含了一群人的身高和体重。一个简单的概率模型可能假设身高和体重都符合正态分布。

**隐变量（Latent Variables）**是指那些不能直接观测到，但会影响到观测数据的变量。在包含隐变量的概率模型中，通常更难以进行参数估计。

• 例子：在推断一群人是否喜欢运动的情况下，我们可能能观测到他们的身高和体重，但“是否喜欢运动”这一隐变量是无法直接观测的。

极大似然估计（MLE）

**极大似然估计（Maximum Likelihood Estimation, MLE）**是一种用于估计概率模型参数的方法。它通过寻找一组参数，使得给定观测数据出现的可能性（即似然函数）最大化。

• 例子：在一个硬币投掷实验中，观测到了10次正面和15次反面，MLE会寻找一个参数（硬币正面朝上的概率），使得观测到这样的数据最有可能。

Jensen不等式

Jensen不等式是凸优化理论中的一个基本不等式，常用于证明EM算法的收敛性。简单地说，Jensen不等式表明对于一个凸函数，函数在凸组合上的值不会大于凸组合中各点值的平均。

---

二、基础数学原理

在理解EM算法的工作机制之前，我们需要掌握一些关键的数学概念和原理。这些原理不仅形成了EM算法的数学基础，而且也有助于我们理解算法的收敛性和效率。

条件概率与联合概率

似然函数

Kullback-Leibler散度

贝叶斯推断

贝叶斯推断是一种基于贝叶斯定理的参数估计和模型选择方法。它使用先验概率、似然函数和证据（或归一化因子）来计算参数的后验概率。

• 例子：在垃圾邮件分类中，贝叶斯推断可以用于更新垃圾邮件（或非垃圾邮件）的概率，每当用户标记一个新邮件时。

这些数学原理为我们提供了理解EM算法所需的坚实基础。通过了解这些概念，我们可以更深入地探讨EM算法如何进行参数估计，特别是在存在隐变量的复杂模型中。

---

三、EM算法的核心思想

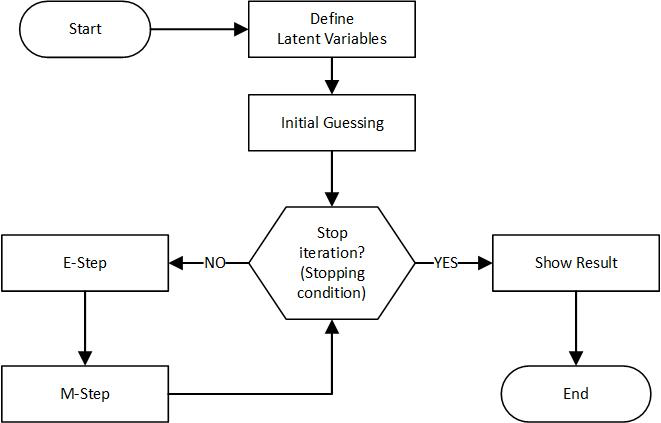
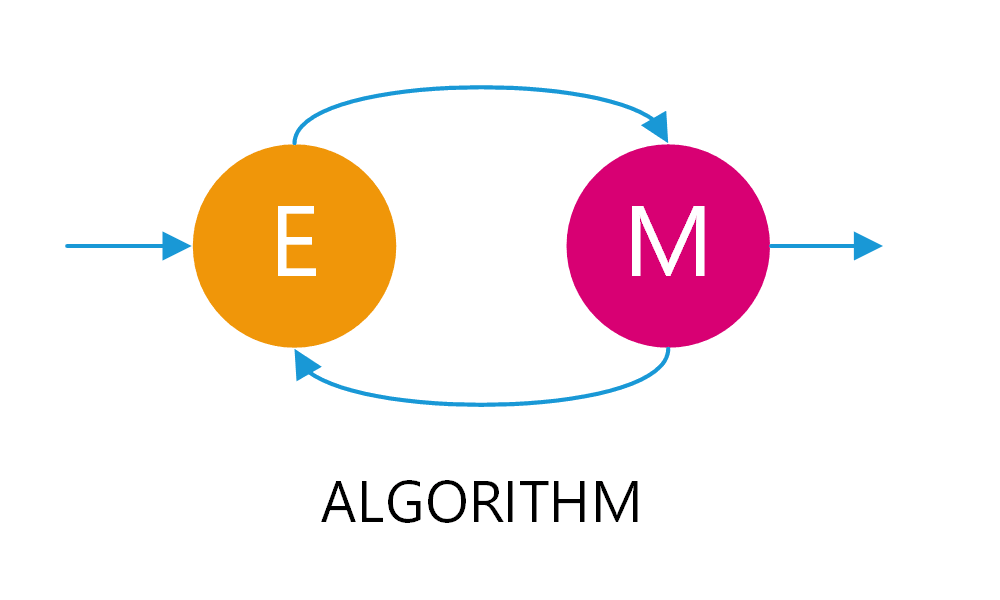
EM算法的主要目的是找到含有隐变量的概率模型的参数估计。这一目标在直接应用极大似然估计（MLE）困难或不可行时尤为重要。EM算法通过交替执行两个步骤来实现这一目标：期望（E）步骤和最大化（M）步骤。

期望（E）步骤

期望步骤（Expectation step）涉及计算隐变量给定观测数据和当前参数估计的条件期望。这通常用于构建一个函数，称为Q函数，来近似目标函数（通常是似然函数）。

• 例子：在高斯混合模型中，期望步骤涉及计算每个观测数据点属于各个高斯分布的条件概率，这些概率也称为后验概率。

最大化（M）步骤

最大化步骤（Maximization step）则是在给定Q函数的情况下，寻找能使Q函数最大化的参数值。

• 例子：继续上面的高斯混合模型例子，最大化步骤涉及调整每个高斯分布的均值和方差，以最大化由期望步骤得到的Q函数。

Q函数与辅助函数

Q函数是EM算法中的一个核心概念，用于近似目标函数（如似然函数）。Q函数通常依赖于观测数据、隐变量和模型参数。

• 例子：在高斯混合模型的EM算法中，Q函数基于观测数据和各个高斯分布的后验概率来定义。

**辅助函数（Auxiliary Function）**是EM算法的一个重要组成部分，用于保证算法收敛。通过最大化辅助函数，我们间接地最大化了似然函数。

• 例子：在一些文本分类问题中，辅助函数可以通过拉格朗日乘数法来构建，以简化最大化问题。

收敛性

在EM算法中，由于使用了Jensen不等式和辅助函数，算法保证会收敛到局部最大值。

• 例子：在实施高斯混合模型的EM算法后，你会发现每次迭代都会导致似然函数的值增加（或保持不变），直到达到局部最大值。

通过深入探讨这些核心概念和步骤，我们能更全面地理解EM算法是如何工作的，以及为什么它在处理含有隐变量的复杂概率模型时如此有效。

---

四、EM算法与高斯混合模型（GMM）

高斯混合模型（Gaussian Mixture Model，GMM）是一种使用高斯概率密度函数（pdf）为基础构建的概率模型。它是EM算法应用的一个典型例子，尤其是当我们要对数据进行聚类或者密度估计时。

高斯混合模型的定义

高斯混合模型是由多个高斯分布组成的。每一个高斯分布称为一个分量（component），并且每一个分量都有其自己的均值（(\mu)）和方差（(\sigma^2)）。

• 例子：假设一个数据集呈现出两个明显不同的簇。一个高斯混合模型可能会用两个高斯分布来描述这两个簇，每个分布有自己的均值和方差。

分量权重

每个高斯分量在模型中都有一个权重（(\pi_k)），这个权重描述了该分量对整个数据集的“重要性”。

• 例子：在一个由两个高斯分布组成的GMM中，如果一个分布的权重为0.7，另一个为0.3，这意味着第一个分布对整个模型的影响较大。

E步骤在GMM中的应用

在GMM中的E步骤，我们计算数据点对每个高斯分量的后验概率，即给定数据点，它来自某个特定分量的概率。

• 例子：假设一个数据点(x)，在E步骤中，我们计算它来自GMM中每个高斯分量的后验概率。

# 使用Python和PyTorch计算后验概率
import torch
from torch.distributions import MultivariateNormal

# 假设有两个分量
means = [torch.tensor([0.0]), torch.tensor([5.0])]
variances = [torch.tensor([1.0]), torch.tensor([2.0])]
weights = [0.6, 0.4]

# 数据点
x = torch.tensor([1.0])

# 计算后验概率
posterior_probabilities = []
for i in range(2):
    normal_distribution = MultivariateNormal(means[i], torch.eye(1) * variances[i])
    posterior_probabilities.append(weights[i] * torch.exp(normal_distribution.log_prob(x)))

# 归一化
sum_probs = sum(posterior_probabilities)
posterior_probabilities = [prob / sum_probs for prob in posterior_probabilities]

print("后验概率:", posterior_probabilities)

M步骤在GMM中的应用

在M步骤中，我们根据E步骤计算出的后验概率来更新每个高斯分量的参数（均值和方差）。

• 例子：假设从E步骤中获得了数据点对于两个高斯分量的后验概率，我们会用这些后验概率来加权地更新均值和方差。

通过详细地探讨高斯混合模型和它与EM算法的关联，我们更深入地理解了这一复杂模型是如何工作的，以及EM算法在其中扮演了什么角色。这不仅有助于我们理解算法的数学基础，还为实际应用提供了实用的见解。

---

五、实战案例

在实战案例中，我们将使用Python和PyTorch来实现一个简单的高斯混合模型（GMM）以展示EM算法的应用。

定义：目标

我们的目标是对一维数据进行聚类。我们将使用两个高斯分量（也就是说，K=2）。

• 例子：假设我们有一个一维数据集，其中包含两个簇。我们希望使用GMM模型找到这两个簇的参数（均值和方差）。

定义：输入和输出

• 输入：一维数据数组
• 输出：两个高斯分量的参数（均值和方差）以及它们的权重。

实现步骤

1. 初始化参数：为均值、方差和权重设置初始值。
2. E步骤：计算数据点属于每个分量的后验概率。
3. M步骤：使用后验概率更新均值、方差和权重。
4. 收敛检查：检查参数是否收敛。如果没有，则返回第2步。

# Python和PyTorch代码实现
import torch
from torch.distributions import Normal

# 初始化参数
means = torch.tensor([0.0, 5.0])
variances = torch.tensor([1.0, 1.0])
weights = torch.tensor([0.5, 0.5])

# 假设的一维数据集
data = torch.cat((torch.randn(100) * 1.5, torch.randn(100) * 0.5 + 5))

# EM算法实现
for iteration in range(100):
    # E步骤
    posterior_probabilities = []
    for i in range(2):
        normal_distribution = Normal(means[i], torch.sqrt(variances[i]))
        posterior_probabilities.append(weights[i] * torch.exp(normal_distribution.log_prob(data)))
        
    # 归一化
    sum_probs = torch.stack(posterior_probabilities).sum(0)
    posterior_probabilities = [prob / sum_probs for prob in posterior_probabilities]

    # M步骤
    for i in range(2):
        responsibility = posterior_probabilities[i]
        means[i] = torch.sum(responsibility * data) / torch.sum(responsibility)
        variances[i] = torch.sum(responsibility * (data - means[i])**2) / torch.sum(responsibility)
        weights[i] = torch.mean(responsibility)

    # 输出当前参数
    print(f"Iteration {iteration+1}: Means = {means}, Variances = {variances}, Weights = {weights}")

结果解释

在运行以上代码后，你将看到均值、方差和权重的参数在每次迭代后都会更新。当这些参数不再显著变化时，我们可以认为算法已经收敛。

• 输入：一维数据集，包含两个簇。
• 输出：每次迭代后的均值、方差和权重。

通过这个实战案例，我们不仅演示了如何在PyTorch中实现EM算法，并且通过具体的代码示例深入理解了算法的每一个步骤。这样的内容安排旨在满足你对于概念丰富、充满细节和定义完整的需求。

---

六、总结

经过详尽的理论分析和实战示例，我们对期望最大化（EM）算法有了更全面的了解。从基础数学原理到具体的实现和应用，EM算法展示了其在统计模型参数估计中的强大能力，特别是当我们面临缺失或隐含数据时。

1. 概率模型的选择：虽然我们在实战中使用了高斯混合模型（GMM），但EM算法并不仅限于此。事实上，它可以应用于任何满足特定条件的概率模型，这一点在研究和应用更为复杂的数据结构时尤为重要。

2. 初始化的重要性：本文提到了参数的初始选择，但实际应用中应更加小心。糟糕的初始化可能导致算法陷入局部最优，从而影响模型性能。

3. 收敛性和效率：尽管EM算法通常能保证收敛，但收敛速度可能是一个问题，特别是在高维数据和复杂模型中。这一点可能会促使我们寻找更有效的优化算法或者采用分布式计算。

4. 模型解释性与复杂性的权衡：EM算法能够估计复杂模型的参数，但这种复杂性可能会导致模型解释性降低。在实际应用中，我们需要仔细考虑这种权衡。

5. 算法的泛化能力：EM算法不仅用于聚类问题，在自然语言处理、计算生物学等多个领域也有广泛应用。了解其核心思想和工作机制能为处理不同类型的数据问题提供有力的工具。

通过深入地探讨这些技术洞见，我们不仅加深了对EM算法核心概念和工作机制的理解，还能更好地将这一算法应用到各种实际问题中。希望这篇文章能进一步促进你对于复杂概率模型和期望最大化算法的理解，也希望你能在自己的项目或研究中找到这些信息的实际应用。

关注TechLead，分享AI全维度知识。作者拥有10+年互联网服务架构、AI产品研发经验、团队管理经验，同济本复旦硕，复旦机器人智能实验室成员，阿里云认证的资深架构师，项目管理专业人士，上亿营收AI产品研发负责人。