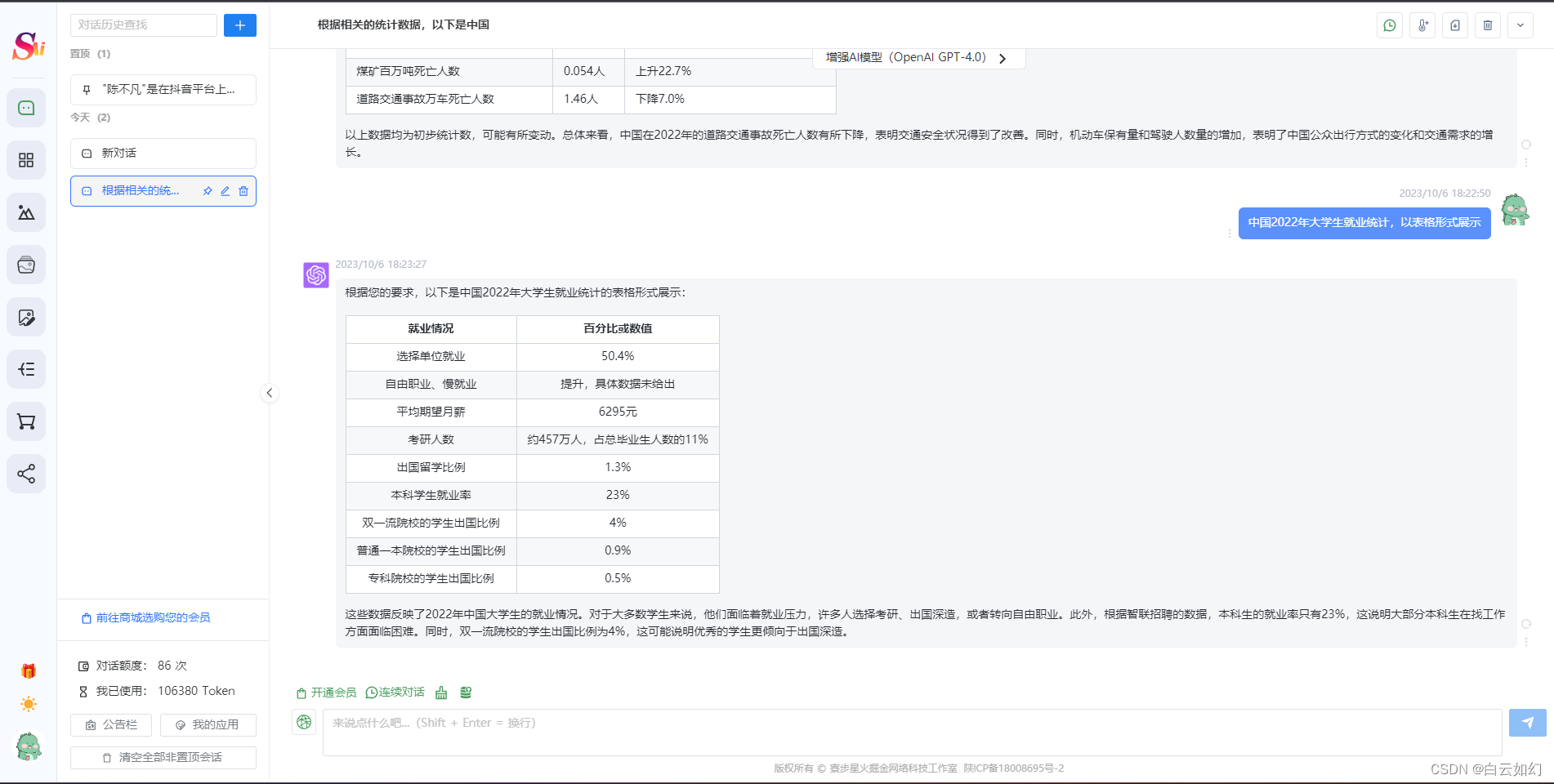
[python 刷题] 4 Median of Two Sorted Arrays

题目：

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be $O(log(m+n))$.

这道题给了两个排序好的数组，然后求有序数组的中位数

这题还是比较难的，我个人觉得直接跳到最优解理解起来会有点吃力，所以就循序从简到繁开始理解起来

暴力解 $(m+n)log(m+n)$

在不考虑时间复杂度为 $O(log(m+n))$ 的情况下，这道题最简单的解法就是合并两个数组，进行排序，找出中位数。即当数组长度为奇数时 $arr[n//2]$，当数组长度为偶数时 $(arr[(n-1)//2]+arr[n//2])/2$，其中 $n$ 为数组的长度。

这样的解法时间复杂度为 $(m+n)log(m+n)$，并不能算是一个非常有效的算法

优化 $(m+n)$

但是已知两个数组都是有序数组，要找的又是中位数，那就可以换个思路去解决这个问题，中位数既然是数组最中间的数字，那也就意味着中位数能够将排序的数组分成 $l$ 和 $r$，其中

• 在有序数组长度和为偶数时，$len(l)=len(r)$
• 在有序数组长度和为奇数时，$len(l)=len(r)-1$

而同样也可以生成两个指针 $ptr1$ 和 $ptr2$ 指向 $m$ 和 $n$，使得 $ptr1+ptr2=len(l)$，这样就能通过 m[ptr1] 和 n[ptr2] 获得中位数

图解一下就是，每次做遍历的时候判断一下当前 ptr 上所对比的两个数字：

当 $A<B$ 时，将 $A$ 所对标的指针指向下一个数字 $C$：

接着对比 $B$ 和 $C$，一直抵达中位数时种植循环。代码如下：

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        n, m = len(nums1), len(nums2)
        i, j = 0, 0
        m1, m2 = 0, 0

        for count in range(0, (n + m) // 2 + 1):
            m2 = m1
            # both array has length
            if i < n and j < m:
                if nums1[i] > nums2[j]:
                    m1 = nums2[j]
                    j += 1
                else:
                    m1 = nums1[i]
                    i += 1
            elif i < n:
                m1 = nums1[i]
                i += 1
            else:
                m1 = nums2[j]
                j += 1

        return m1 if (n + m) % 2 else (m1 + m2) / 2

这样优化下来的时间复杂度为 $O(m+n)$，空间复杂度为 $O(1)$，并且这个解法是能过的，不过我不确定在服务器忙的时候会不会 timeout

优化 $log(m+n)$

上面的解法是从下标为 0 开始进入循环的，但是反过来从 $len(arr)-1$ 做循环也可以，现在就有了几个先决条件：

• l = 0
• r = len(arr) - 1
• 中位数 (mid)

再加上题目中 $O(log(m+n))$ 的提示，接下来就开始捋 binary search 的解法

即同样采用 优化 $(m+n)$ 的解法，不过这里对比一个数字一个数字的对比，这里直接选取较短数组的中位数开始对比，只要额外满足 $max(l_a,l_b)\le min(r_a,r_b)$ 这一条件，就能够保证已经找到对应的中位数，如：

这个时候判断 $m1$ 和 $m2$ 的大小，就可以对整个数组进行对半切割，进行下一步查找，从而达成 $log(min(m,n))$ 的时间复杂度

另外这里其实需要用 4 个指针进行交错对比：

才能更好判断从哪里开始切割

另外，针对可能存在较短数组只存在于一边的 cluster，如 A=[8], B=[1,1,2,2,3,3,4,5] 这种情况，需要进行一个下标的判断，同时辅以默认值

代码如下：

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        a, b = nums1, nums2
        total = len(nums1) + len(nums2)
        half = total // 2

        if len(b) < len(a):
            a, b = a, b

        l, r = 0, len(a) - 1
        while True:
            i = (l + r) // 2  # a
            j = half - i - 2  # b

            a_left = a[i] if i >= 0 else float("-infinity")
            a_right = a[i + 1] if (i + 1) < len(a) else float("infinity")
            b_left = b[j] if j >= 0 else float("-infinity")
            b_right = b[j + 1] if (j + 1) < len(b) else float("infinity")

            # partition is correct
            if max(a_left, b_left) <= min(a_right, b_right):
                # odd
                if total % 2:
                    return min(a_right, b_right)
                # even
                return (max(a_left, b_left) + min(a_right, b_right)) / 2
            elif a_left > b_right:
                r = i - 1
            else:
                l = i + 1