一、贪心算法的定义

贪心算法是指不考虑整体上的综合最优决策，而在局部上以最优决策来解决问题，即每次选择的都是最优的解决方案，不考虑该决策对整体的影响。这种方法在处理一些情况下，可以得到最优解的很好近似方案，例如，哈夫曼编码、求最小生成树中的普里姆算法（Prim）、克鲁斯卡尔算法（Kruskal）、求单源最短路径中的迪杰斯特拉算法（Dijkstra）等算法。

二、贪心算法的基本步骤

• 首先，对整体最优解采用贪心算法进行分解，将其化为若干个小规模的子问题，这些子问题是相互独立的，然后通过数学归纳法证明，在每一步的选择中，可以依据贪心策略在当前子问题中选择出最优解（局部解决，不考虑整体情况，只考虑当前），最后，将所有子问题的最优解进行整体合并，得到整体的最优解，从而解决问题，简单可归纳为三个步骤。

三、贪心算法的性质

贪心算法具有以下两大性质，若针对某一问题，若具有以下重要性质，则可以通过使用贪心算法可以得到最优解。

（一）最优子结构性质

针对一个问题，将问题分为若干个子问题，从而该问题的最优解分割成若干个子问题的最优解来解决，然后通过递推从而得到该问题的最优解，即最优子结构性质。所以，具有这种性质的问题，才能保证通过贪心算法得到的解是最优解。【可分割，局部】

（二）贪心选择性质

在求解问题时，每一步都采取在当前情况下最优的选择，即每次选择都是在局部中选择最优解，从而最终得到的解是整体最优解（最近似），即贪心选择性质。【局部最优】

四、贪心算法的应用

在《数据结构》中贪心算法的常见应用场景有以下，例如，哈夫曼树中的哈夫曼编码，图的应用中求最小生成树以及求单源最短路径的相关算法。

（一）哈夫曼树——哈夫曼编码

注：求哈夫曼编码时，最小频率和最小权值等同，这里以最小权值为例介绍。
简单的来说，哈夫曼编码是可变字长编码(VLC)的一种，常用于数据的压缩，压缩率在20%~90%。哈夫曼树以及哈夫曼编码的基本概念，可以回顾一下之前的文章：数据结构学习笔记——哈夫曼树

例如，画出以3，4，6，8，12，13，15，18，25，40为结点权值所构造的哈夫曼树，并对各结点编码。

解：选取权值最小的两个结点：3和4，相加3+4=7，新的根结点为7，将其插入到树的集合中：

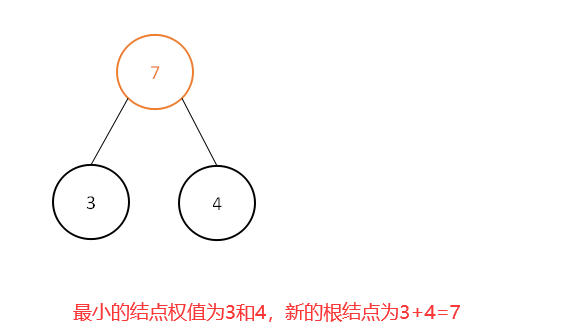
此时集合中为[6，7，8，12，13，15，18，25，40]，继续选取最小的两个结点权值：

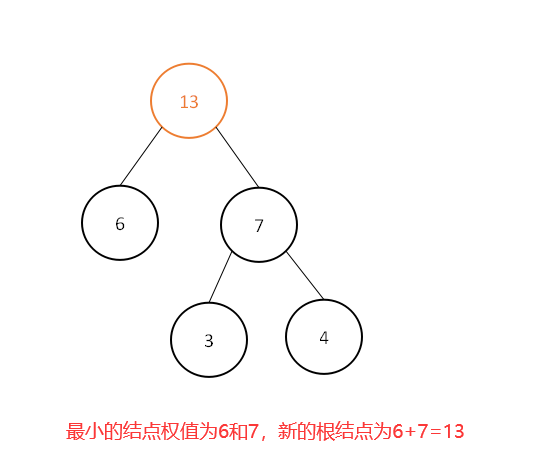
此时集合中为[8，12，13，13，15，18，25，40]，继续选取最小的两个结点权值：

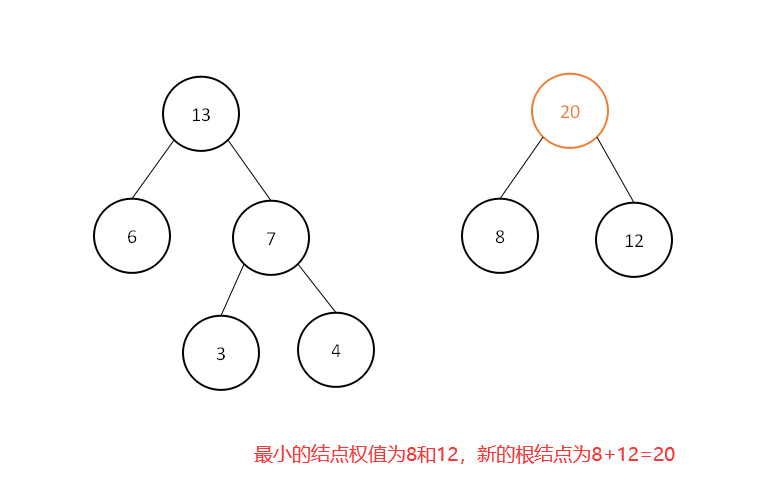
此时集合中为[13，13，15，18，20，25，40]，继续选取最小的两个结点权值：

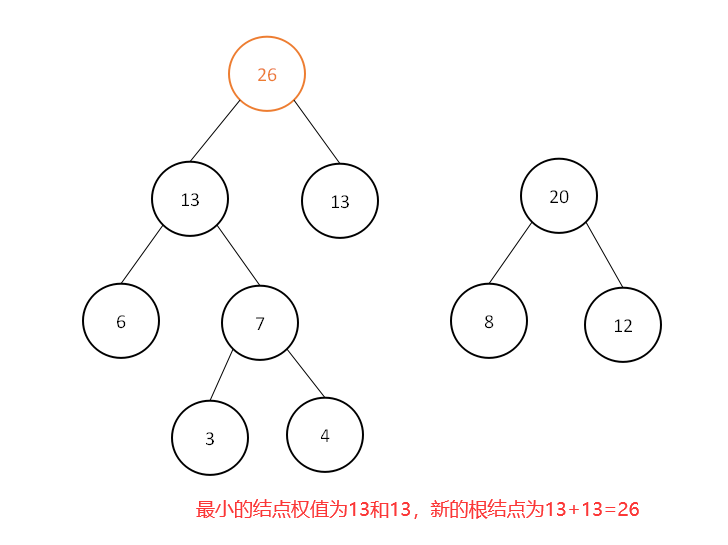
此时集合中为[15，18，20，25，26，40]，继续选取最小的两个结点权值：

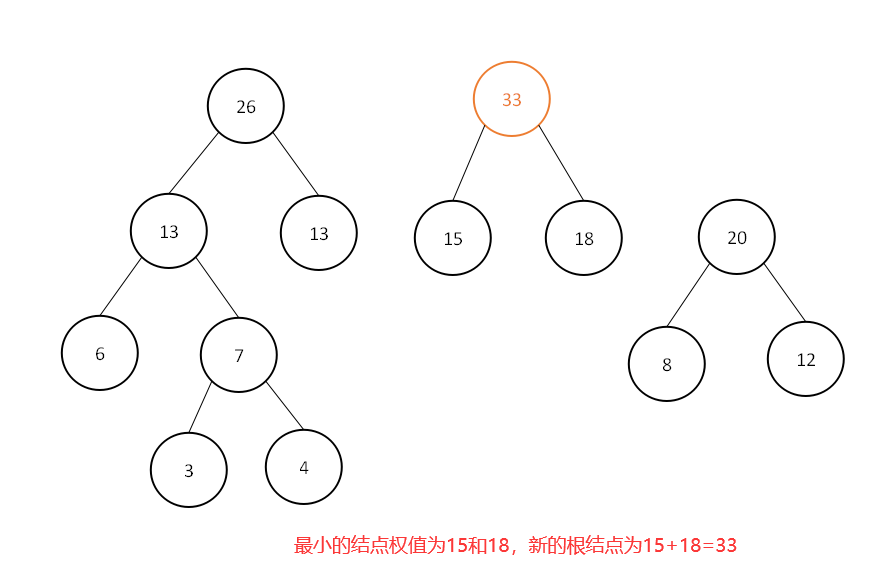
此时集合中为[20，25，26，33，40]，继续选取最小的两个结点权值：

此时集合中为[26，33，40，45]，继续选取最小的两个结点权值：

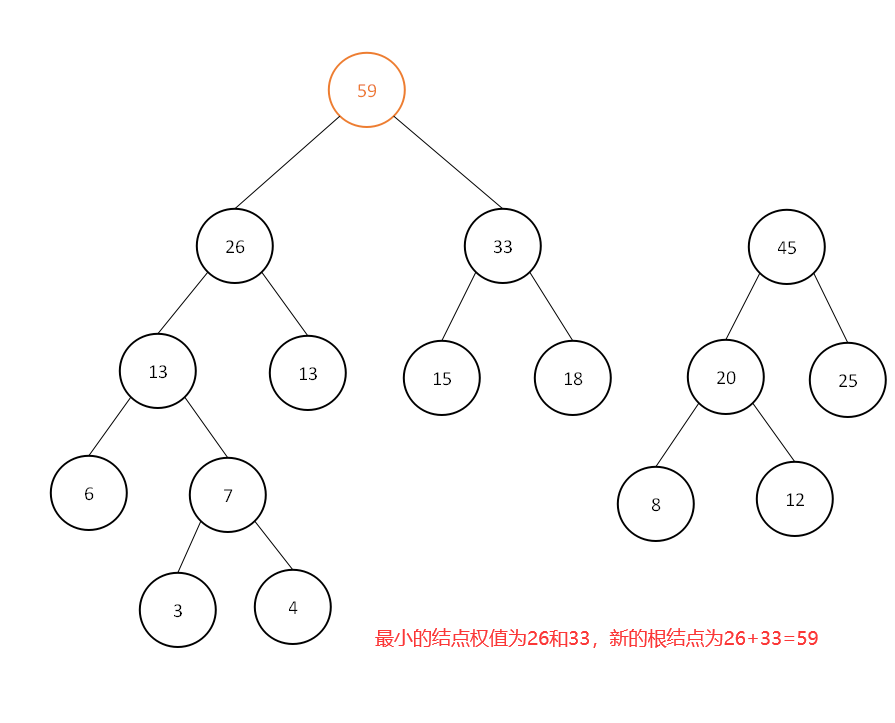
此时集合中为[40，45，59]，继续选取最小的两个结点权值：

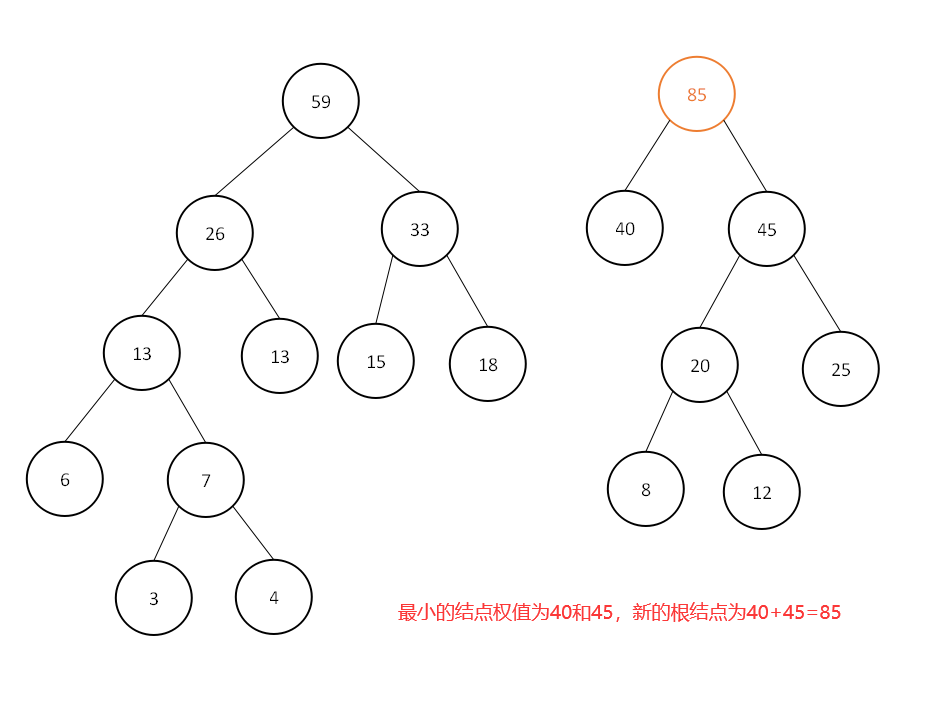
此时集合中为[59，85]，继续选取最小的两个结点权值：

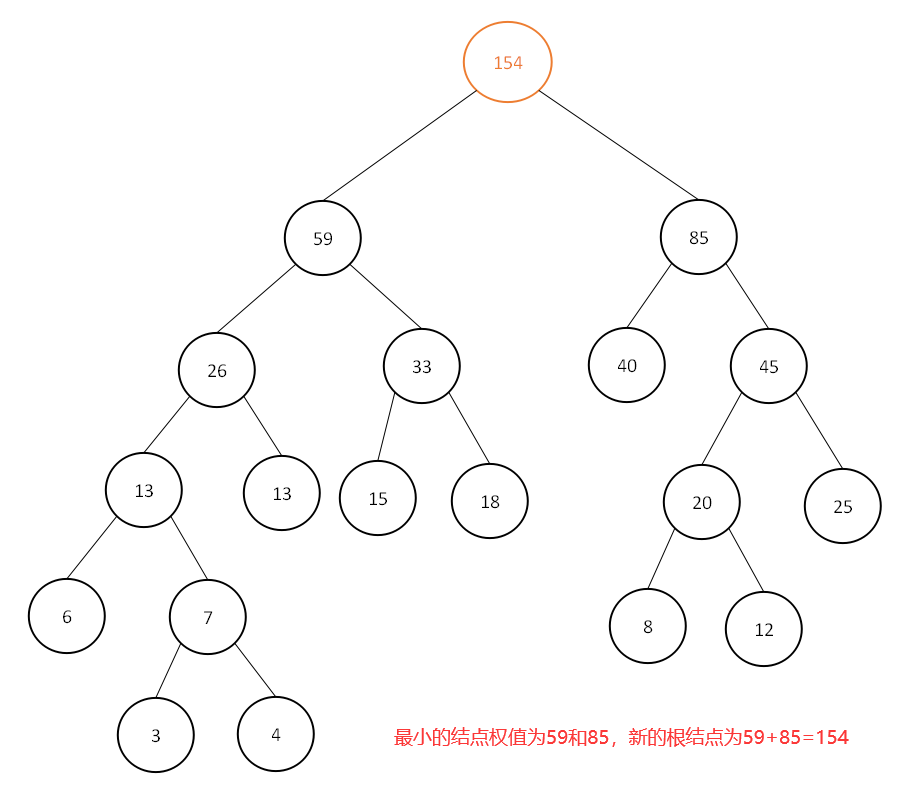
即为最终的哈夫曼树，设左分支为0，右分支为1，如下：

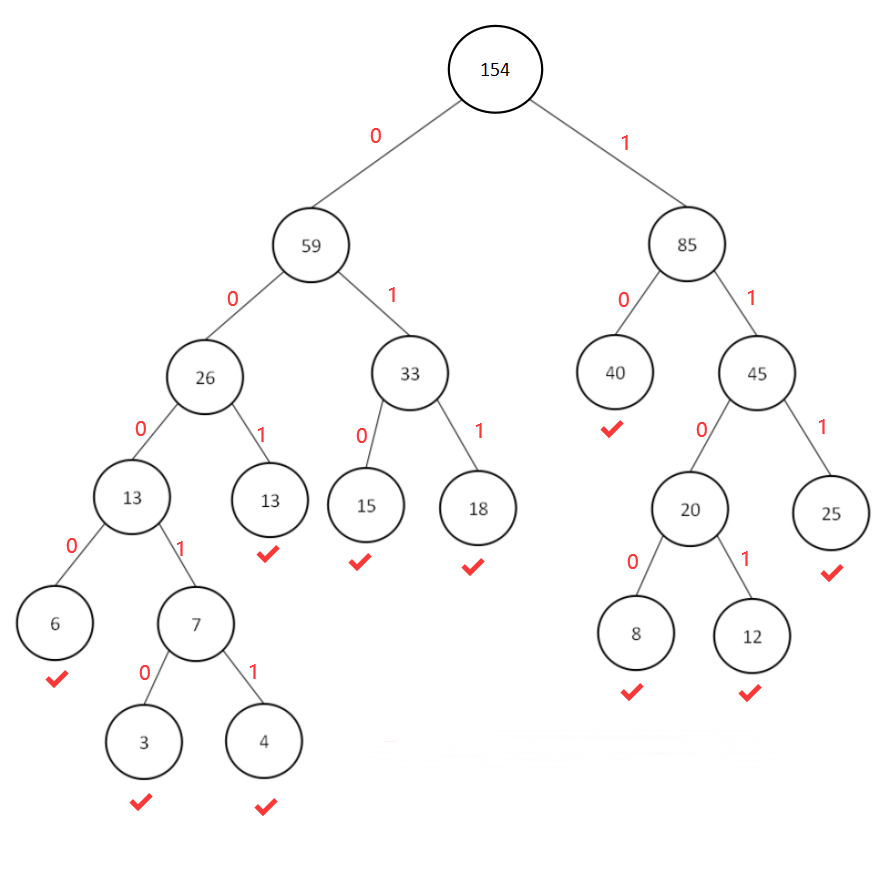
则各叶子结点的哈夫曼编码如下：
3：00010
4：00011
6：0000
8：1100
12：1101
13：001
15：010
18：011
25：111
40：10

从以上过程中，不难看出，每次的选择都是选取两棵根结点权值最小的树作为左、右子树，新的二叉树的根结点权值为其权值之和，然后将原先两个结点从森林中删除，新的结点添加进去……，按照由下至上依次构造哈夫曼树，最上层的权值最大。
1、哈夫曼编码的最优子结构性质

• 针对哈夫曼树，对字符进行编码，将要编码的字符作为叶子节点，两两组合，从下往上，通过执行n-1次的合并产生新的根结点，依次进行下去，得到最终的哈夫曼编码。由于每次选择的都是两个最小权值结点，从而构成了一个局部最优解。【局部最优】

n个结点的哈夫曼树可形成共2n-1个结点，且叶子结点的个数也为n，分支结点的个数=总结点数-叶子结点数=2n-1-n=n-1，即有n-1次合并。

2、哈夫曼编码的贪心选择性质

• 每次选择当前两个或权值最小的结点构造一颗子树的根结点，其权值为权值之和，并把产生的子树的根结点再插入到队列中，最后，按结点的权值大小为最小优先队列。由于每次选择的情况都是最小权值结点，所以这两个结点之和一定是最优解。【选择最优】

（二）图的应用——求最小生成树

简单的来说，含有n个顶点的最小生成树有以下特点：
①最小生成树不唯一；
②最小生成树是一个无环图（不形成回路）；
③最小生成树中包含图的所有顶点；
④最小生成树在所有生成树中该树的各边权值之和最小；
⑤最小生成树生成树的边的个数为n-1；

在生成最小生成树时可以选择不同的边，所以最小生成树不唯一（存在权值相同的边），但若当图G的各边权值不同，则此时最小生成树是唯一的，所以最小生成树的边的权值之和总是唯一的。

最小生成树的概念，可以回顾一下之前的文章：数据结构学习笔记——图的应用1（最小生成树、最短路径）

1、普里姆算法（Prim）

普里姆算法的步骤如下：
①从顶点集V中任意选取一个顶点，然后将与该顶点邻接的边中选取一条权值最小的边，将其并入，从而得到一棵树；
②继续选取邻接的边中最短的边（权值最小），连接边，并入树中（若有相同权值，则任选一条即可）；
③直到图中的所有顶点都被并入，得到最小生成树。

• 普里姆算法适用于求边稠密的网的最小生成树，由于每次都是选择一个点与其他剩下点的之间的最短边（最小权值），所以其时间复杂度与图的边数无关，核心语句是在集顶点集V中寻找最近的顶点，所以n个顶点、e条边的无向连通带权图，其时间复杂度为O(n²)。

例如，下面是一个无向带权连通图，采用普里姆算法生成最小生成树：

任意选取一个顶点为起点开始，这里选取V1为例。

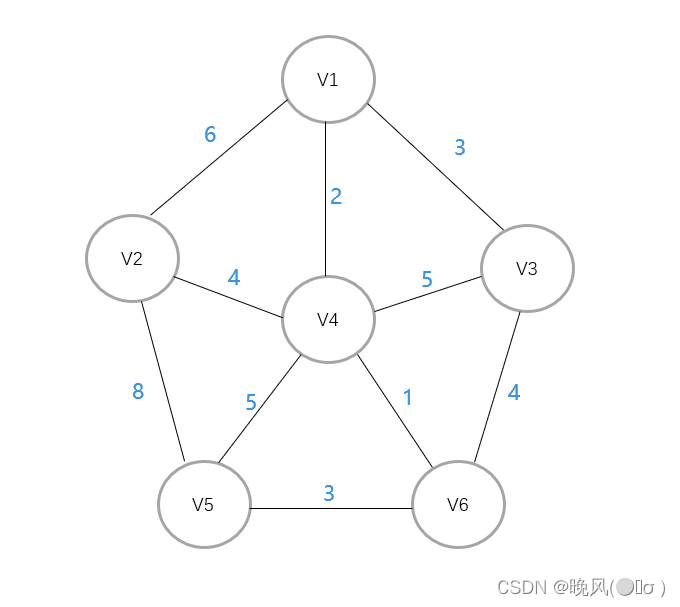
此时邻接的边的权值分别为[2、3、6]，取最小权值2，所以V1与邻接的顶点V4相连：

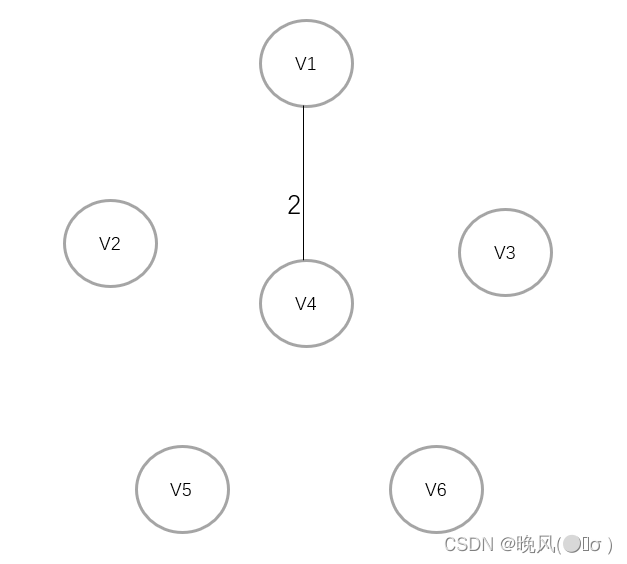
此时邻接的边的权值分别为1、4、5、5，以及加上前面的3、6，即[1、3、4、5、5、6]，取最小权值1，所以V4与邻接的顶点V6相连：

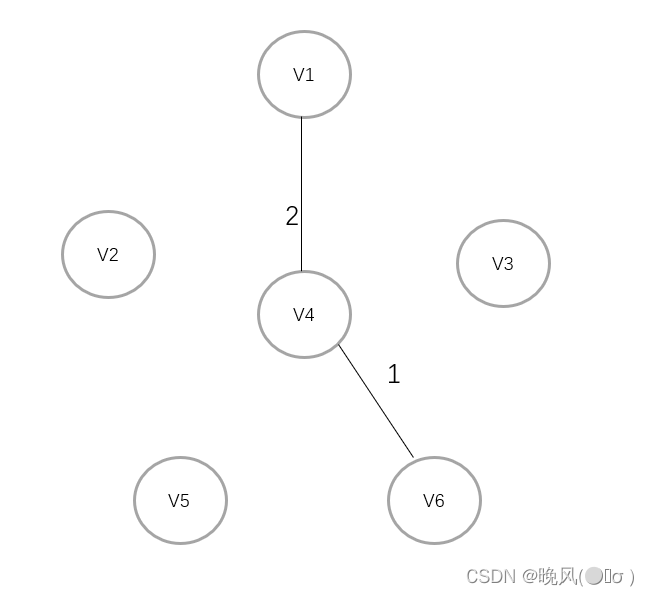
此时邻接的边的权值分别为3、4，以及加上前面的3、6、4、5、5，即[3、4、4、5、5、6]，取最小权值3，V6与邻接的顶点V5相连：

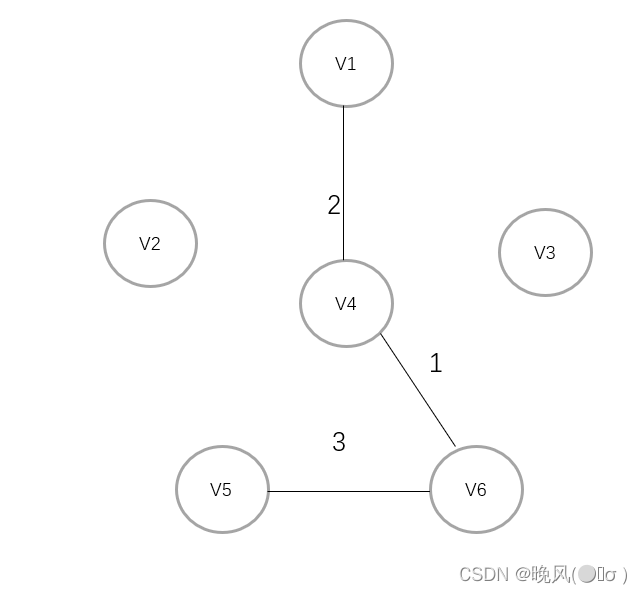
取此时最小权值，取的是当前图中剩余各边对应权值中最小的权值，即3，V1与V3相连：

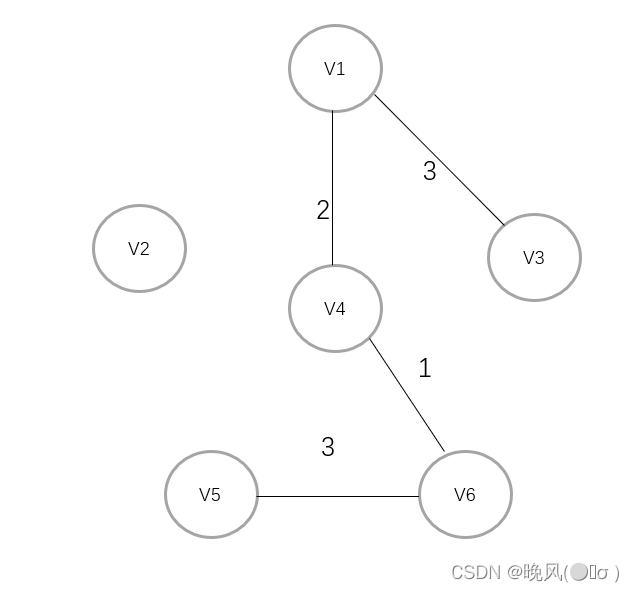
取此时最小权值，即4，V4与V2相连，至此所有顶点都被访问到，得到最小生成树（该最小生成树的代价为3+1+4+2+3=13）：

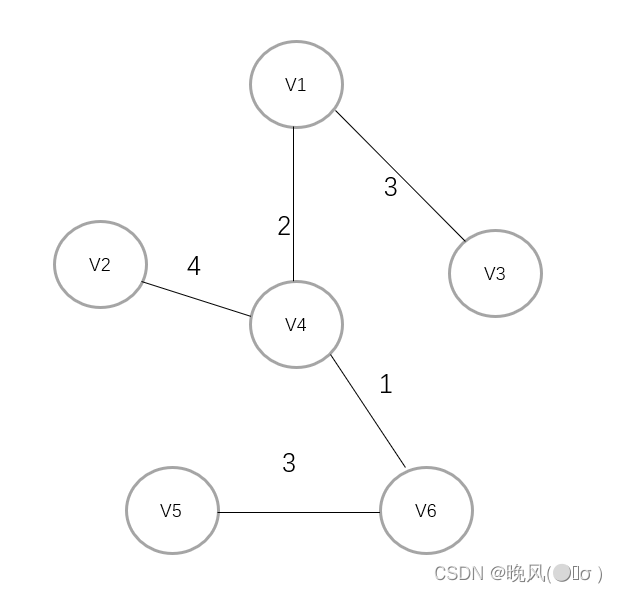
（1）普里姆算法的最优子结构性质

• 从上可看出，普里姆算法的核心是每次选择当前顶点（连通）与剩下顶点（未连通）之间的最小权值的边，依次进行，每次选最小，最后得到一棵最小生成树。由于每次选择两个最小权值边，从而构成了一个局部最优解。【局部最优】

（2）普里姆算法的贪心选择性质

• 由于在每次选择中，都是选择的权值最小的边，所以保证了每一步的选择情况都是当前最优的，从而最终得到的是一棵最小生成树。【选择最优】

2、克鲁斯卡尔算法（Kruskal）

克鲁斯卡尔算法的步骤如下：
①先将图的所有边对应的权值按照从小到大的顺序排序；
②选择其中权值最小的边加入并连接，并入树中，若选取的某边与先前的树构成回路（环），则舍去；
③一直进行下去，权值以小到大，直到所有顶点被访问到，得到最小生成树。

• 克鲁斯卡尔算法适用于求边稀疏的网的最小生成树，核心语句是将e条边从小到大依次排序，所以n个顶点、e条边的无向连通带权图，其时间复杂度为O(eloge)。

例如，下面是一个无向带权连通图，采用克鲁斯卡尔算法生成最小生成树：

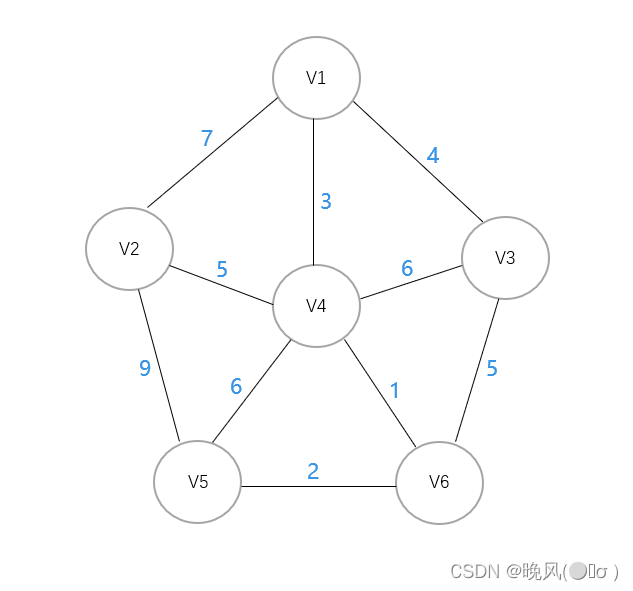
将图中所有边对应的权值，按从小到大排序如下：1，2，3，4，5，6，8。
可知权值1最小，首先连接V4和V6：

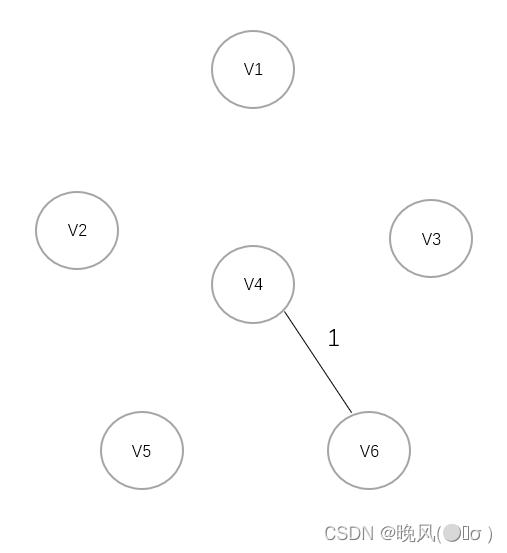
3、选择权值2，连接V6与V5：

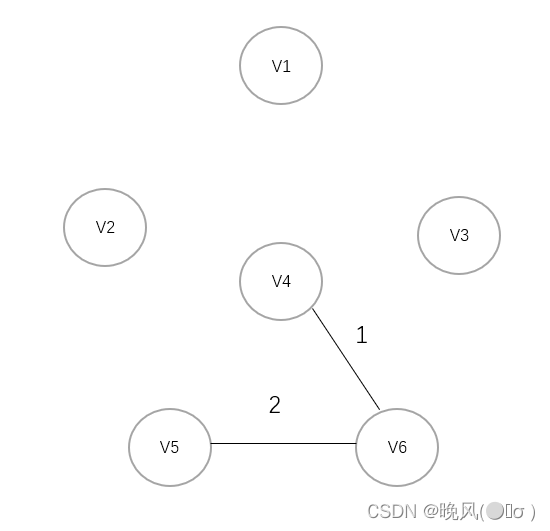
3、选择权值3，选取V4与V1连接：

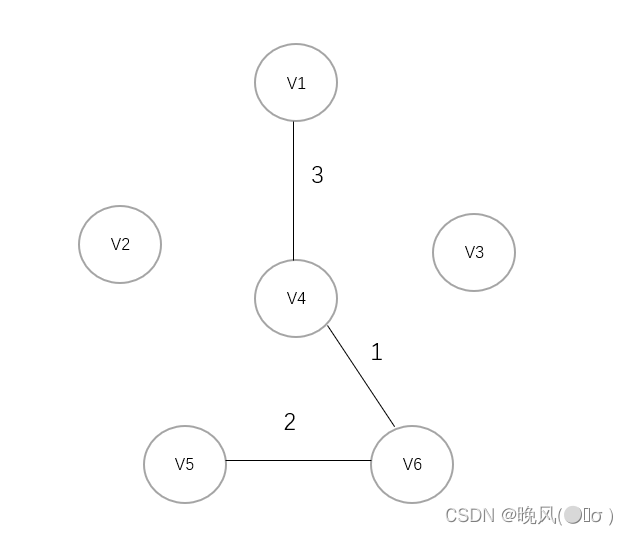
4、选择权值4，连接V1与V3：

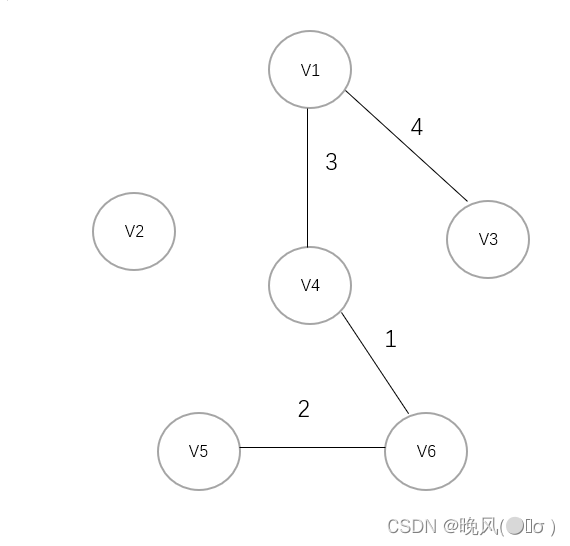
5、选取权值5，连接V4与V2，最终得到最小生成树如下（该最小生成树的代价为4+3+1+5+2=15）：

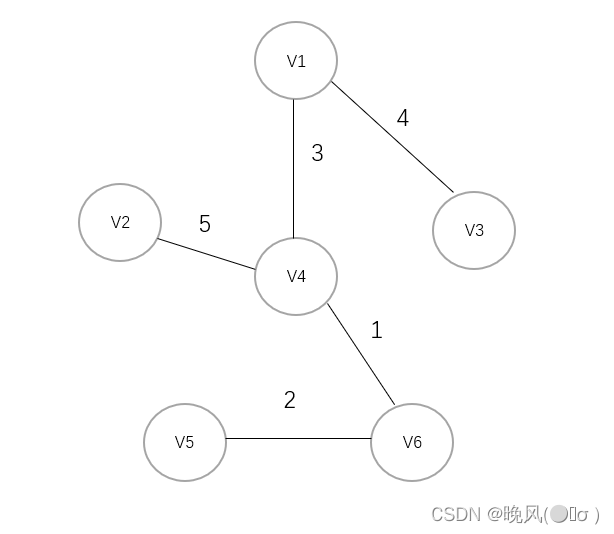
（1）克鲁斯卡尔算法的最优子结构性质

• 克鲁斯卡尔算法中由于权值已经顺序排列，所以依次进行，每次加入的都是当前最小的边，构成的都是当前的一个连通分量的最小生成树（该顶点到其他顶点的最小生成树），最后得到整个图的最小生成树。由于事先已排序好，每次选择的是当前最小权值边，从而构成了一个局部最优解。【局部最优】

（2）克鲁斯卡尔算法的贪心选择性质

• 由于在每次选择中，都是选择的权值最小的边且保证不会成回路（环），若不满足该条件，则说明当前情况不是最优，所以保证了在每一步的选择情况都是当前最优的，从而最终得到的是一棵最小生成树。【选择最优】

3、两种算法的比较

名称	比较
普里姆算法	一次次
克鲁斯卡尔算法	整体

普里姆算法是每次选取一个最短边，即针对顶点，只能得到该顶点到其他顶点的最小生成树，当需要求图的最小生成树时，需要一次次的普里姆算法才能得到最小生成树，而克鲁斯卡尔算法由于一开始就将边的权值按从小到大依次排序，是从整体上出发，所以可以直接得到最小生成树，另外，由于需要对所有的边进行排序，其占用的空间也比普里姆算法多，空间复杂度为O(n)。

（三）图的应用——求单源最短路径

迪杰斯特拉算法（Dijkstra）

迪杰斯特拉算法计算的是在一个有向带权图中，指定一个源点到其他所有顶点的最短路径长度，即最短路径，而单源最短路径一般通过迪杰斯特拉算法解决。

在带权图中，一个顶点到另一个顶点所经过边的权值之和称为该路径的带权路径长度，由于可能路径不止一条，所以将带权路径长度最短的那条路径称为最短路径。

迪杰斯特拉算法的步骤如下：
①通过一个数组存储源点到每个顶点的距离；
②依次选取源点当前未访问到的所有顶点中距离最短的顶点，然后更新该顶点相邻的顶点与源点的距离；
③重复过程，直到所有顶点都被访问到。

• 克鲁斯卡尔算法中的核心语句是寻找距离源点最近的顶点，所以n个顶点的有向带权图，其时间复杂度为O(n²)，另外由于需要数组存放带权邻接矩阵，所以空间复杂度为O(n)。

（1）迪杰斯特拉算法的最优子结构性质

• 在每次更新该顶点相邻的顶点与源点的距离时，当前所有的顶点与源点的最短路径是最优的，从而构成了一个局部最优解。【局部最优】

（2）迪杰斯特拉算法的贪心选择性质

• 由于每次选择的都是源点当前未访问到的所有顶点中距离最短的顶点，保证选择的都是当前距离最短，从而得到的是最短路径。【选择最优】