背包问题
- 一、背包问题概述
- 二、01背包问题
- (1)求这个背包至多能装多大价值的物品?
- (2)若背包恰好装满,求至多能装多大价值的物品?
- 三、完全背包问题
- (1)求这个背包至多能装多大价值的物品?
- (2)若背包恰好装满,求至多能装多大价值的物品?
一、背包问题概述
背包问题是⼀种组合优化的问题。问题可以描述为:给定⼀组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。
根据物品的个数,分为如下几类:
- 01背包问题:每个物品只有⼀个
- 完全背包问题:每个物品有无限多个
- 多重背包问题:每件物品最多有 x 个
- 混合背包问题:每个物品会有上面三种情况
- 分组背包问题:物品有 n 组,每组物品里有若干个,每组里最多选⼀个物品
其中上述分类里面,根据背包是否装满,又分为两类:
- 不一定装满背包
- 背包一定装满
根据限定条件的个数,又分为两类:
- 限定条件只有⼀个:比如体积 -> 普通的背包问题
- 限定条件有两个:比如体积 + 重量 -> 二维费用背包问题
虽然背包问题种类非常繁多,题型非常丰富,难度也是非常难以捉摸。但是,它们都是从 01背包问题 演化过来的。01 背包问题 非常重要。
二、01背包问题
01背包 — 模板
Nowcoder -DP41.01背包
题目:你有一个背包,最多能容纳的体积是V。
现在有 n 个物品,第 i 个物品的体积为 vi,价值为 wi.
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
输入描述:
第一行两个整数 n 和 V,表示物品个数和背包体积。
接下来 n 行,每行两个数 vi 和 wi,表示第i个物品的体积和价值。
1 ≤ n, V, vi, wi ≤ 1000
输出描述:
输出有两行,第一行输出第一问的答案,第二行输出第二问的答案,如果无解请输出0。
(1)求这个背包至多能装多大价值的物品?
- 状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积「不超过」 j ,所有的选法中,能挑选出来的最大价值。 - 状态转移方程:
线性 dp 状态转移方程分析方式,⼀般都是根据「最后⼀步」的状况,来分情况讨论:
a. 不选第 i 个物品:相当于就是去前 i - 1 个物品中挑选,并且总体积不超过 j 。此时 dp[i][j] = dp[i - 1][j] ;
b. 选择第 i 个物品:那么我就只能去前 i - 1 个物品中,挑选总体积不超过 j - v[i] 的物品。此时 dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。但是这种状态不⼀定存在,因此需要特判⼀下。
具体来说,如下图:

- 初始化:
我们多加一行,方便我们的初始化,此时仅需将第⼀行初始化为 0 即可。因为什么也不选,也能满足体积不小于 j 的情况,此时的价值为 0 。
综上,状态转移方程为: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])
第一问的核心代码如下:
// 第一问
// dp[i][j] 表示:从前 i 个物品中挑选,总体积「不超过」 j ,所有的选法中,能挑选出来的最⼤价值
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= V; j++)
{
dp[i][j] = dp[i - 1][j];
if (j - v[i] >= 0)
dp[i][j] = max(w[i] + dp[i - 1][j - v[i]], dp[i][j]);
}
}
cout << dp[n][V] << endl;
(2)若背包恰好装满,求至多能装多大价值的物品?
第⼆问仅需微调⼀下 dp 过程的细节即可,因为有可能凑不齐 j 体积的物品,因此我们把不合法的状态设置为 -1.
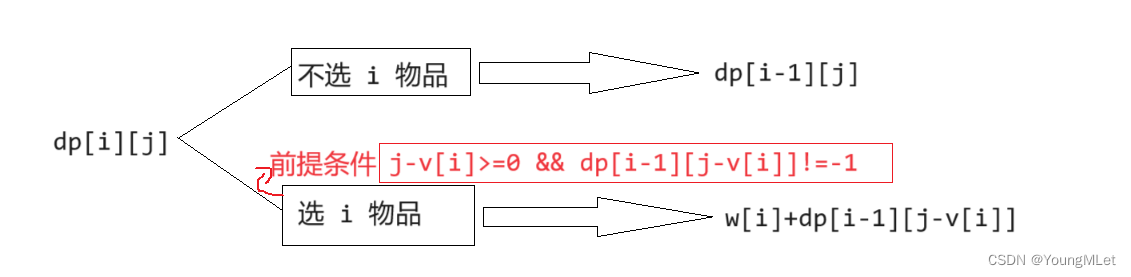
- 状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积「正好」等于 j ,所有的选法中,能挑选出来的最大价值。 - 状态转移方程:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]) . 但是在使用 dp[i - 1][j - v[i]] 的时候,不仅要判断 j >= v[i] ,还要判断 dp[i -1][j - v[i]] 表示的情况是否存在,也就是 dp[i - 1][j - v[i]] != -1.
我们可以表示为下图的:
- 初始化:
我们多加一行,方便我们的初始化:
i. 第⼀个格子为 0 ,因为正好能凑齐体积为 0 的背包;
ii. 但是第一行后面的格子都是 -1 ,因为没有物品,无法满足体积大于 0 的情况,如下图所示,dp 表完成初始化:
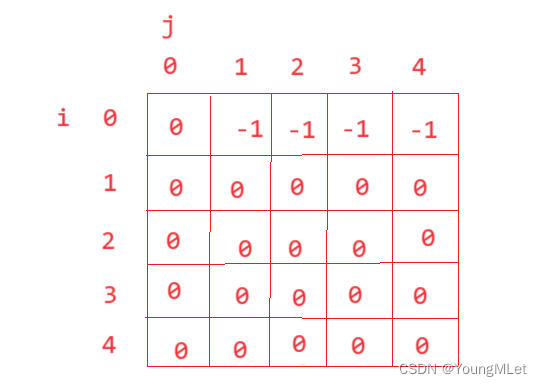
所以第二问的核心代码如下:
// 第二问
// dp[i][j] 表⽰:从前 i 个物品中挑选,总体积「正好」等于 j ,所有的选法中,能挑选出来的最⼤价值。
memset(dp, 0, sizeof(dp));
// 值为 -1 表示从 0~i 的物品中没有体积刚好为 j 的物品,所以也就没有价值
for (int j = 1; j <= V; j++) dp[0][j] = -1;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= V; j++)
{
dp[i][j] = dp[i - 1][j];
if (j - v[i] >= 0 && dp[i - 1][j - v[i]] != -1)
dp[i][j] = max(dp[i][j], w[i] + dp[i - 1][j - v[i]]);
}
}
cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;
空间优化:
背包问题基本上都是利用 「滚动数组」 来做空间上的优化:
i. 利用「滚动数组」优化;
ii. 直接在「原始代码」上修改。
根据状态转移方程,我们更新当前 dp 表位置的时候,只需要用到 i - 1 行中的第 j 个位置和第 j - v[i] 个位置,如下图,三角形是我们需要更新的位置,我们只需要两个圆圈的位置:

我们可以观察到,三角形所在的位置只需要依赖第 j 个位置和第 j - v[i] 个位置,所以我们可以大胆把横坐标去掉,只需要一个维度的坐标即可,这种方法叫做滚动数组;但是我们要注意,遍历顺序需要从右往左,如下图:
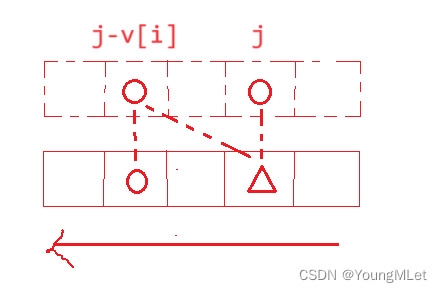
因为我们依赖的是当前未更新的 dp 表的位置和当前位置左边的位置,如果从左往右更新,那么对于后面的位置来说,它们的左边位置已经被覆盖了,所以我们应该从右往左更新。
所以在01背包问题中,优化的结果为:
i. 删掉所有的横坐标;
ii. 修改⼀下 j 的遍历顺序
优化后的整体代码:
#include <vector>
#include <algorithm>
#include <string.h>
#include <iostream>
using namespace std;
const int N = 1001;
int n, V, v[N], w[N];
int dp[N];
// 对空间进行优化:使用滚动数组
int main()
{
cin >> n >> V;
for (int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
// 第一问
// dp[i][j] 表⽰:从前 i 个物品中挑选,总体积「不超过」 j ,所有的选法中,能挑选出来的最⼤价值
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= v[i]; j--) // 遍历顺序修改成从右往左
dp[j] = max(w[i] + dp[j - v[i]], dp[j]);
}
cout << dp[V] << endl;
// 第二问
// dp[i][j] 表⽰:从前 i 个物品中挑选,总体积「正好」等于 j ,所有的选法中,能挑选出来的最⼤价值。
memset(dp, 0, sizeof(dp));
// 值为 -1 表示从 0~i 的物品中没有体积刚好为 j 的物品,所以也就没有价值
for (int j = 1; j <= V; j++) dp[j] = -1;
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= v[i]; j--)
if (dp[j - v[i]] != -1)
dp[j] = max(dp[j], w[i] + dp[j - v[i]]);
}
cout << (dp[V] == -1 ? 0 : dp[V]) << endl;
return 0;
}
有关01背包的练习题:
Leetcode -416.分割等和子集
Leetcode -494.目标和
Leetcode -1049.最后一块石头的重量Ⅱ
三、完全背包问题
完全背包 — 模板
Nowcoder -DP42.完全背包
题目:你有一个背包,最多能容纳的体积是V。
现在有 n 种物品,每种物品有任意多个,第 i 种物品的体积为 vi, 价值为 wi.
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
输入描述:
第一行两个整数 n 和 V,表示物品个数和背包体积。
接下来 n 行,每行两个数 vi 和 wi,表示第i种物品的体积和价值。
1 ≤ n, V ≤ 1000
输出描述:
输出有两行,第一行输出第一问的答案,第二行输出第二问的答案,如果无解请输出0。
(1)求这个背包至多能装多大价值的物品?
- 状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积不超过 j ,所有的选法中,能挑选出来的最大价值。(这里是和 01背包⼀样) - 状态转移方程:线性 dp 状态转移⽅程分析方式,⼀般都是根据最后⼀步的状况,来分情况讨论。但是最后⼀个物品能选很多个,因此我们的需要分很多情况:
a. 选 0 个第 i 个物品:此时相当于就是去前 i - 1 个物品中挑选,总体积不超过 j 。此时最大价值为 dp[i - 1][j] ;
b. 选 1 个第 i 个物品:此时相当于就是去前 i - 1 个物品中挑选,总体积不超过 j - v[i] 。因为挑选了⼀个 i 物品,此时最大价值为 dp[i - 1][j - v[i]] + w[i] ;
c. 选 2 个第 i 个物品:此时相当于就是去前 i - 1 个物品中挑选,总体积不超过 j - 2 * v[i] 。因为挑选了两个 i 物品,此时最大价值为 dp[i - 1][j - 2 * v[i]] + 2 * w[i] ;
d. …
如下图:
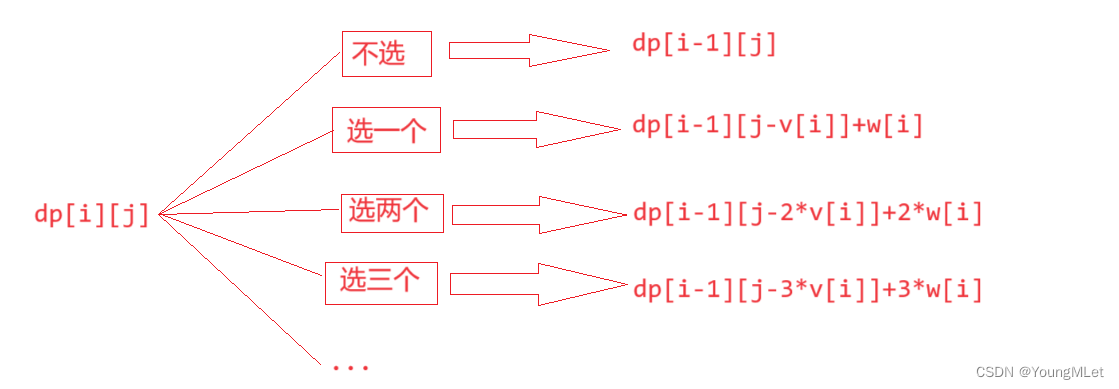
此时我们可以如下分析:

我们观察到,画绿色下划线的内容中,下面的下划线中的 dp 表达式与上面的只相差一个 w[i] ,所以,紫色框框中的 dp[i][j-v[i]] 加上一个 w[i] 是可以完全替代上面的紫色框框中的一堆表达式,所以我们得出以下状态转移方程:
dp[i][j] = max(dp[i-1][j], dp[i][j-v[i]]+w[i])
- 初始化:
我们多加⼀行,方便我们的初始化,此时仅需将第⼀行初始化为 0 即可。因为什么也不选,也能满足体积不小于 j 的情况,此时的价值为 0 。
所以第一问的核心代码如下:
// 第一问
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= V; j++)
{
dp[i][j] = dp[i - 1][j];
if(j >= v[i]) dp[i][j] = max(dp[i][j - v[i]] + w[i], dp[i][j]);
}
}
cout << dp[n][V] << endl;
(2)若背包恰好装满,求至多能装多大价值的物品?
第⼆问仅需微调⼀下 dp 过程的细节即可,因为有可能凑不齐 j 体积的物品,因此我们把不合法的状态设置为 -1 。
-
状态表示:
dp[i][j] 表示:从前 i 个物品中挑选,总体积正好等于 j ,所有的选法中,能挑选出来的最大价值。 -
状态转移方程:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]) ;但是在使用 dp[i][j - v[i]] 的时候,不仅要判断 j >= v[i] ,还要判断 dp[i][j - v[i]] 表示的情况是否存在,也就是 dp[i][j - v[i]] != -1. -
初始化:
我们多加一行,方便我们的初始化:
a. 第⼀个格子为 0 ,因为正好能凑齐体积为 0 的背包;
b. 但是第一行后面的格子都是 -1 ,因为没有物品,无法满足体积大于 0 的情况。
所以第二问的核心代码如下:
// 第二问
memset(dp, 0, sizeof(dp));
dp[0][0] = 0;
for(int j = 1; j <= V; j++)
dp[0][j] = -1;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= V; j++)
{
dp[i][j] = dp[i - 1][j];
if(j >= v[i] && dp[i][j - v[i]] != -1) dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);
}
}
cout << (dp[n][V] == -1? 0 : dp[n][V]) << endl;
空间优化: 滚动数组,注意,根据状态转移方程,我们这里需要更新的位置是依赖 i - 1 行的第 j 个位置和第 i 行的 j - v[i] 个位置,而 dp[i][j-v[i]] 是已经更新过的位置,所以我们需要从右往左更新 dp 表;
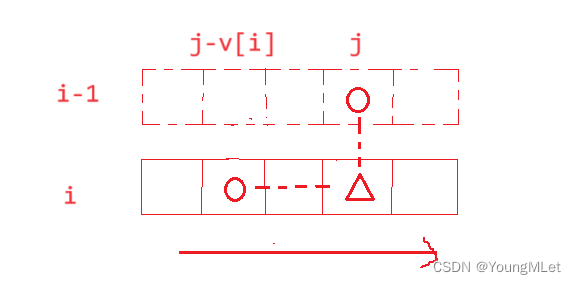
空间优化后的整体代码:
#include <iostream>
#include <string.h>
using namespace std;
const int N = 1001;
int n, V, v[N], w[N];
int dp[N];
// 空间优化后的代码
int main()
{
cin >> n >> V;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
// 第一问
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= V; j++)
{
if(j >= v[i]) dp[j] = max(dp[j - v[i]] + w[i], dp[j]);
}
}
cout << dp[V] << endl;
// 第二问
memset(dp, 0, sizeof(dp));
dp[0] = 0;
for(int j = 1; j <= V; j++)
dp[j] = -1;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= V; j++)
{
if(j >= v[i] && dp[j - v[i]] != -1) dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
}
cout << (dp[V] == -1? 0 : dp[V]) << endl;
}
完全背包的练习题:
Leetcode -322.零钱兑换
Leetcode -518.零钱兑换Ⅱ
Leetcode -279.完全平方数
此外,我们还有一些⼆维费用的背包问题练习:
Leetcode -474.一零和
Leetcode -879.盈利计划