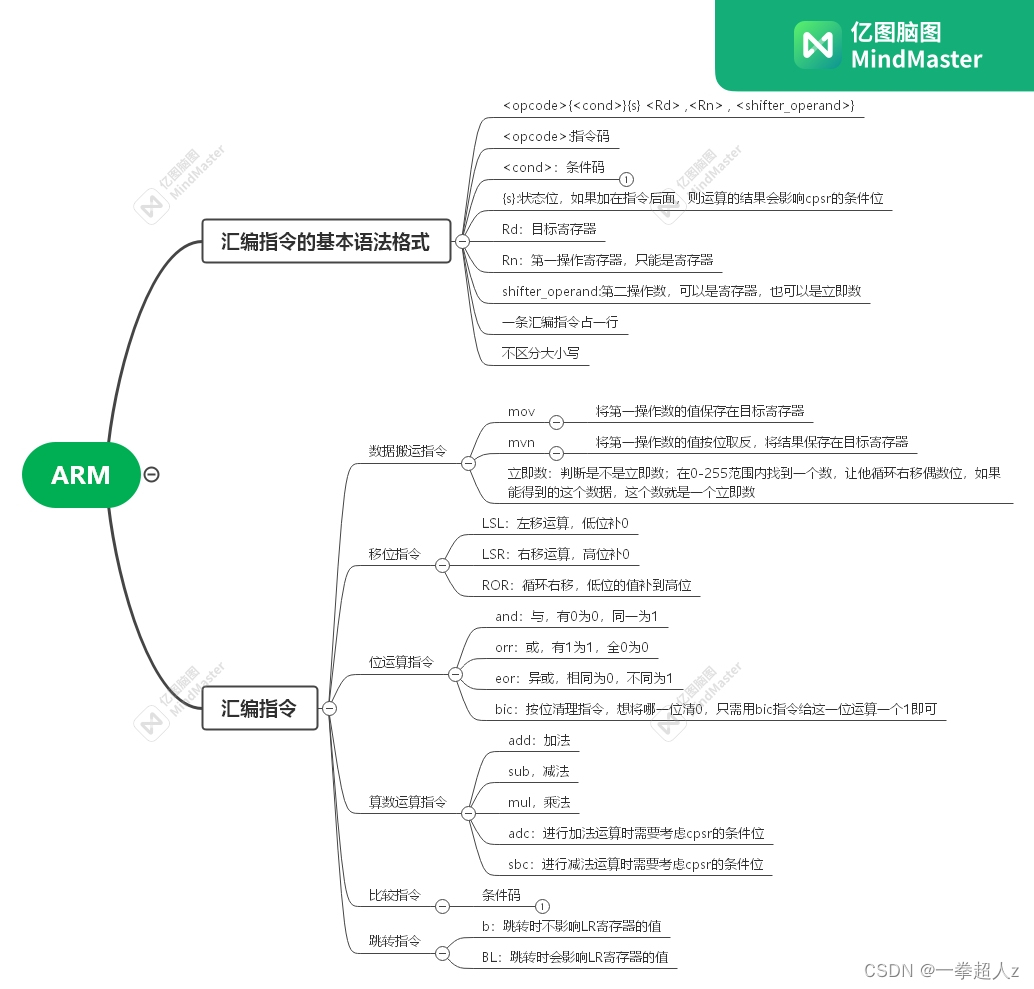
介绍协向量时,曾说过它们有点像 行向量, 行向量确实以某种方式代表了协向量,
这里说明一下:
协向量是不变的; 协向量组件是可变的。

协向量不依赖坐标系,协向量的组件取决于坐标系。
当我们说协向量具有组件时,我们的意思是?

要记住:协向量是 一个 从向量到实数的函数,协向量并不存在向量空间V中,协向量只是将V中的向量作为输入,所以我们不能使用V中的基向量来构造协向量,
所以应该怎么做才对?

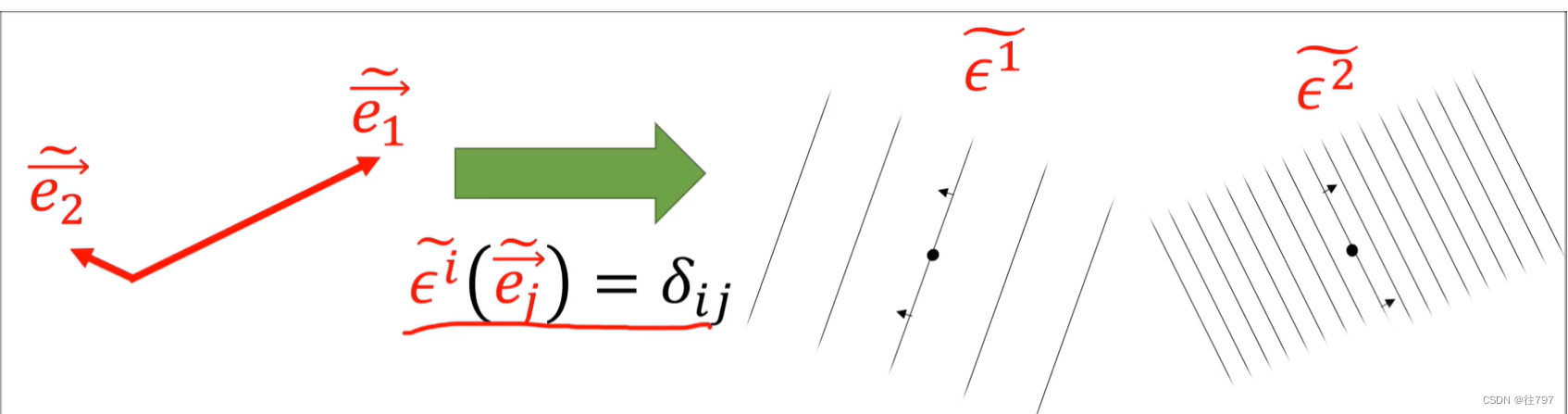
从V中取两基向量,并引入两个协向量(从向量到实数的函数),
并定义它们的计算结果,
如图: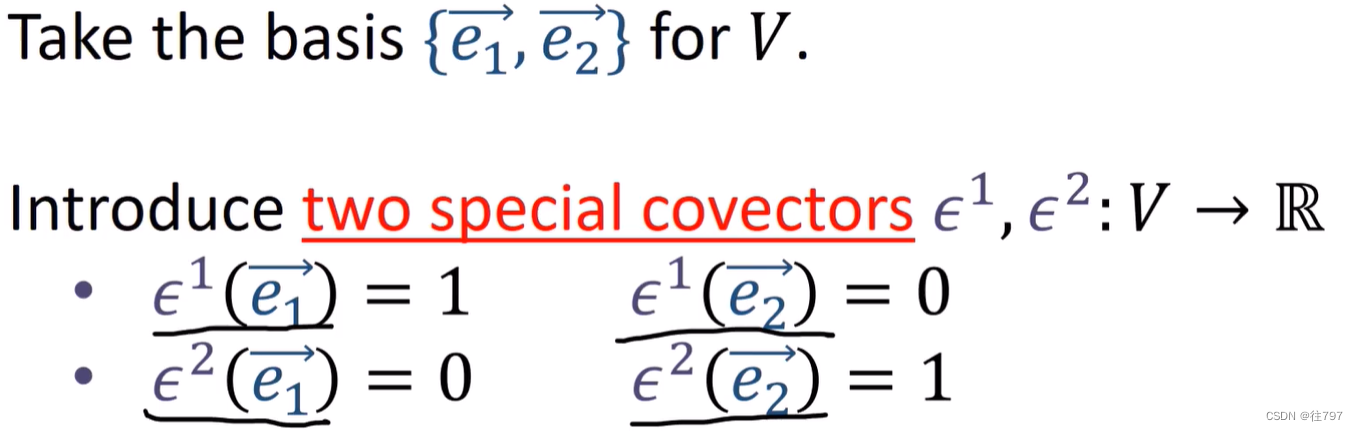
还记得那个 kronecker Delta 吗。
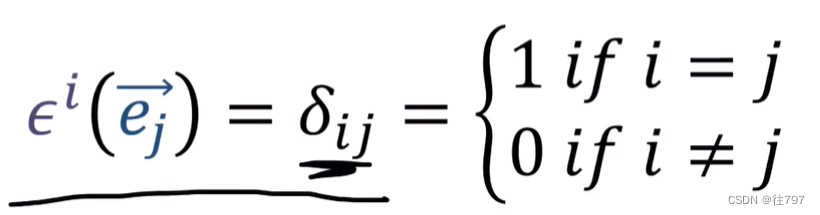
这些协向量 实际上看起来像一堆线吗? 为找到答案,把它们作用到某个向量v上,
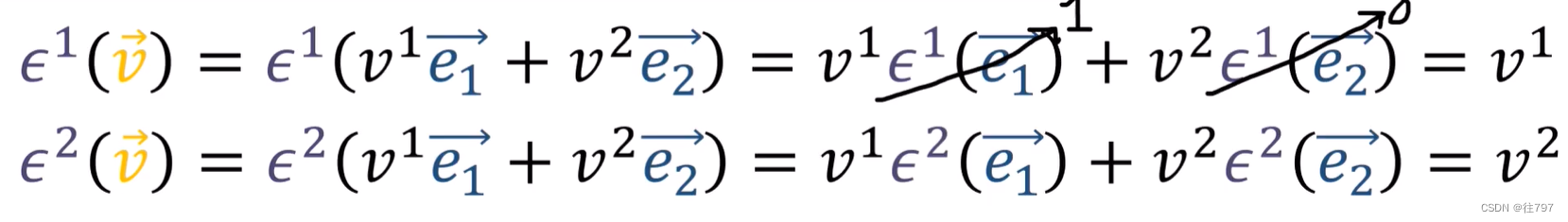
仔细 看,这些 所做的是:它们在投射矢量分量,是把?
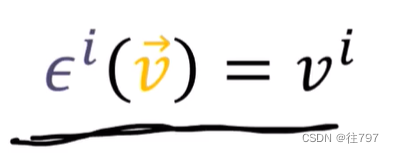
当把应用到v中,我们将得到v基向量e1、e2上的组件,
所以,看起来就像是:可以帮助我们获得向量v的第一个分量,其中e1就是指向这个分量的方向。
看起来就像是:可以帮助我们获得向量v的第2个分量,其中e2就是指向这个分量的方向。
这就是协向量的样子(视觉上)

现在我们对向量v应用一些通用的协向量α,α可以是任一协向量
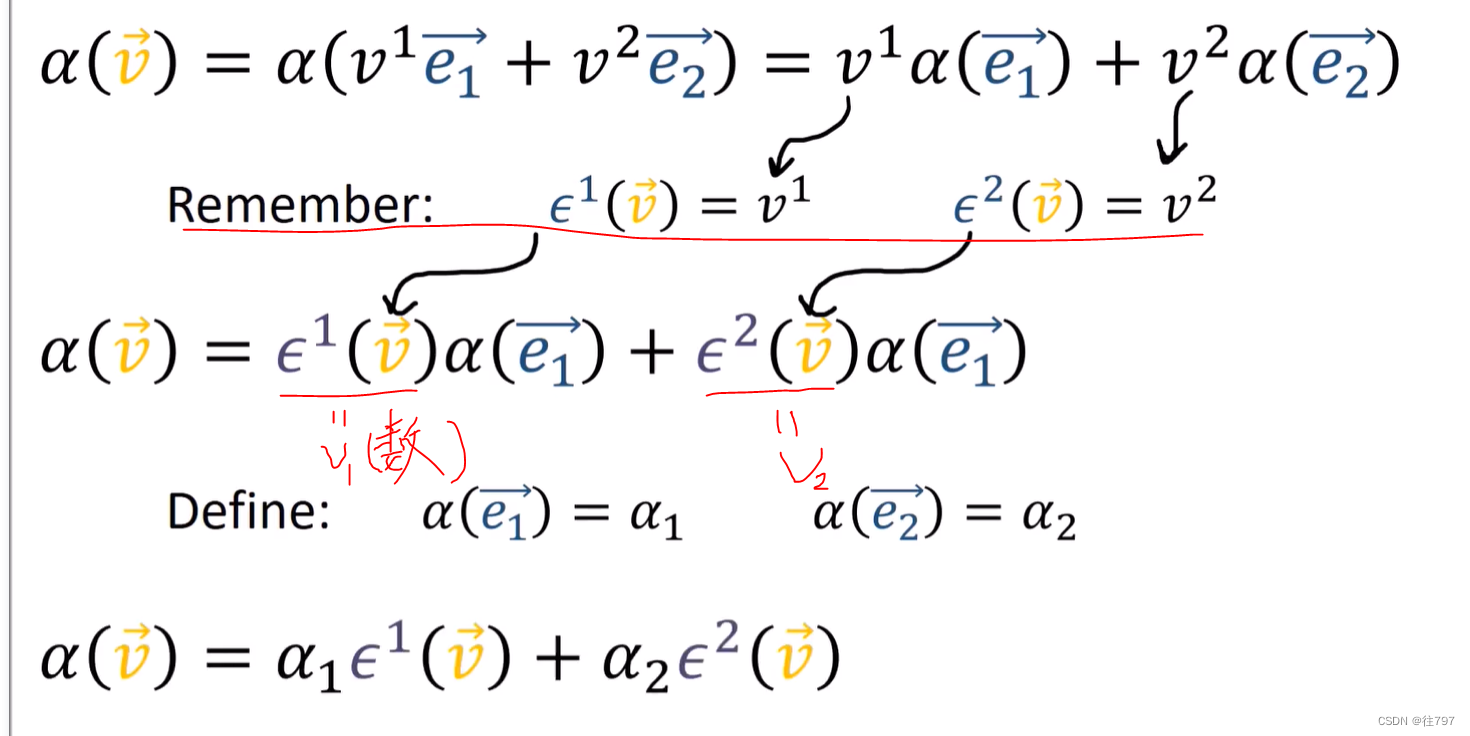
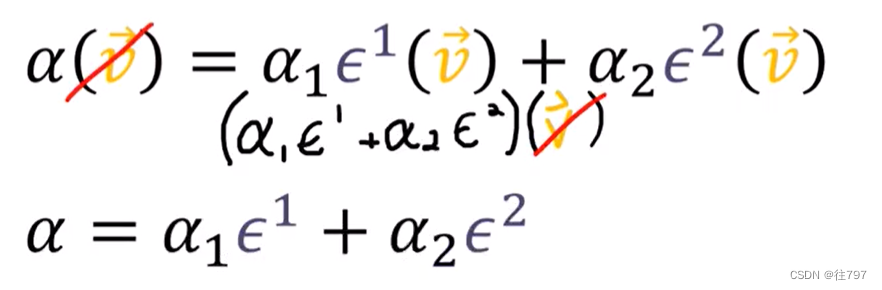
(注:α1=α*e1=一个数,α2也是一个数,上面表示 任意一个协向量α = 数1* + 数2*
)
所以上面我们所作的是:编写了一个通用的协向量α(α可以是任意协向量) 作为协向量的线性组合,
所以这意味着协向量 是 构成了所有协向量集合的基底,
也因为这个原因,被称为 ”对偶基“ , 因为它们是对偶空间V* 上的 基底。
以上我们就用了代数的方式写出了 一个协向量的表达,
现考虑视觉上,
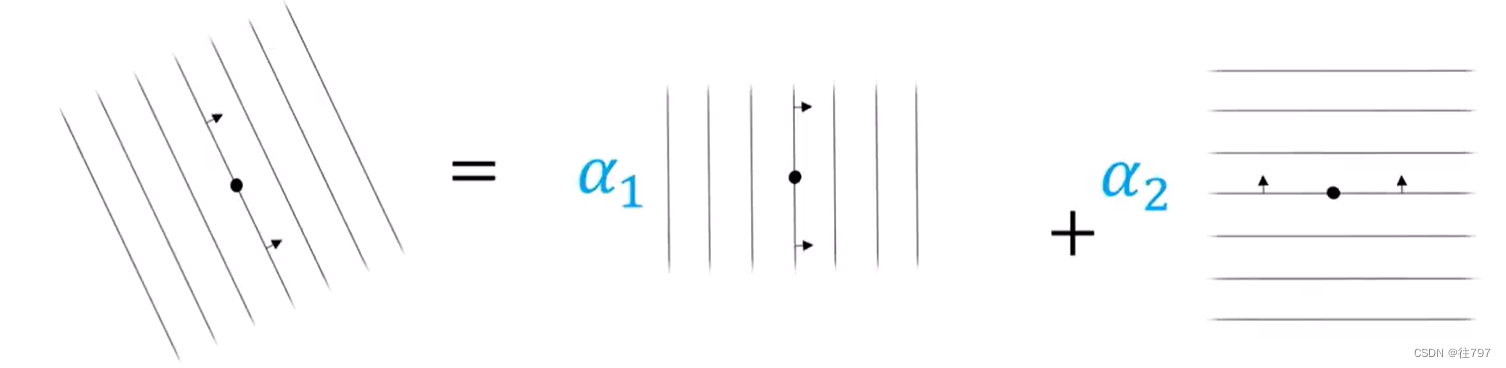
假设有一个协向量α,一簇在e1、e2为基底的向量空间的线, 可通过把α应用到基底e1、e2上来获得α的组件,只需计算穿透的行数,
我们可以把α写成、
的线性组合 的方式来表示α。
所以过程就是:从基底向量开始,使用这个定义 来获得对偶协向量的基底,然后使用 这些 我们就可以将任意的协向量表示为对偶基的线性组合。(这是对上面整个过程的描述)
但记住,、
并不是 唯一的基底,(正如向量空间那般,基底可以变,基底个数不变那般)
因此,我们可以用别的向量开始,如:
并使用以下规则,我们可以定义另一对对偶基,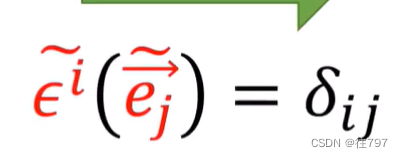 (规则--就是规定)
(规则--就是规定)
同样地,可将任意协向量α表示为 、
的线性组合。

例子:
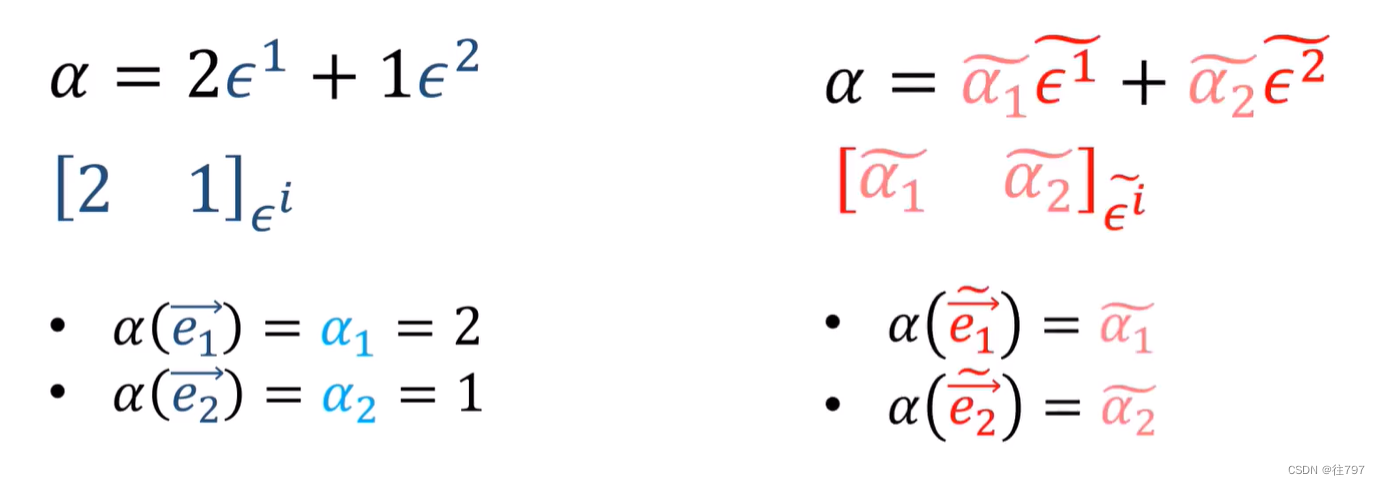
已知一个协向量α在 旧(对偶)基、
下的线性表示, 同时有一对新(对偶)基
、
,想把协向量α利用新基
、
做线性表示,
将α应用到新基底,
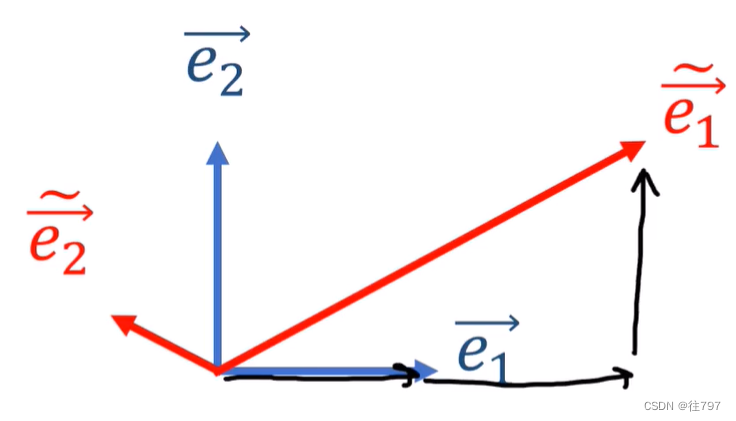
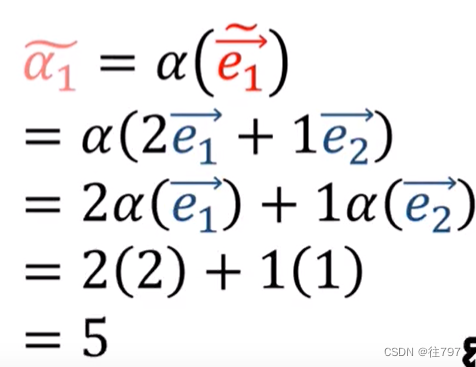
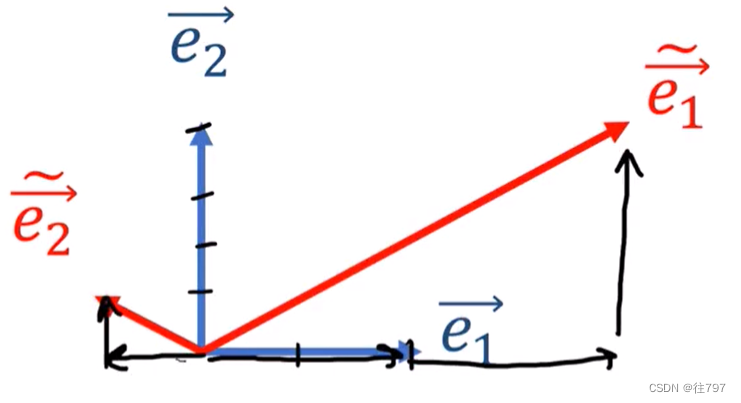
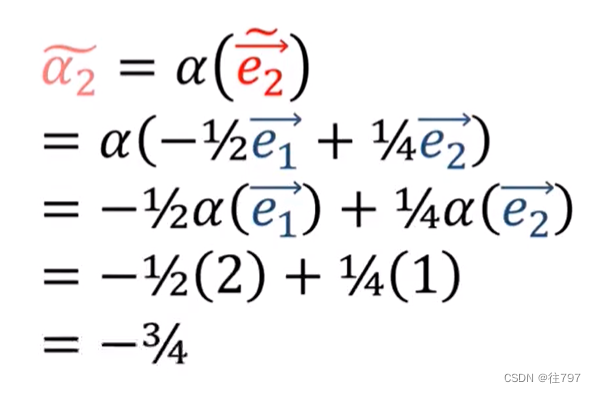
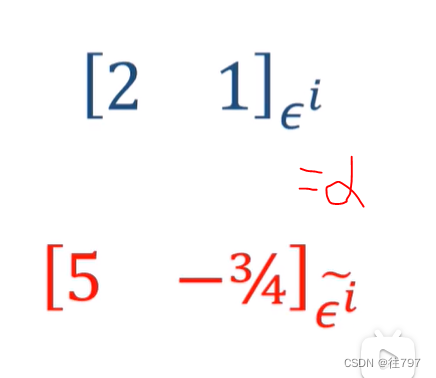
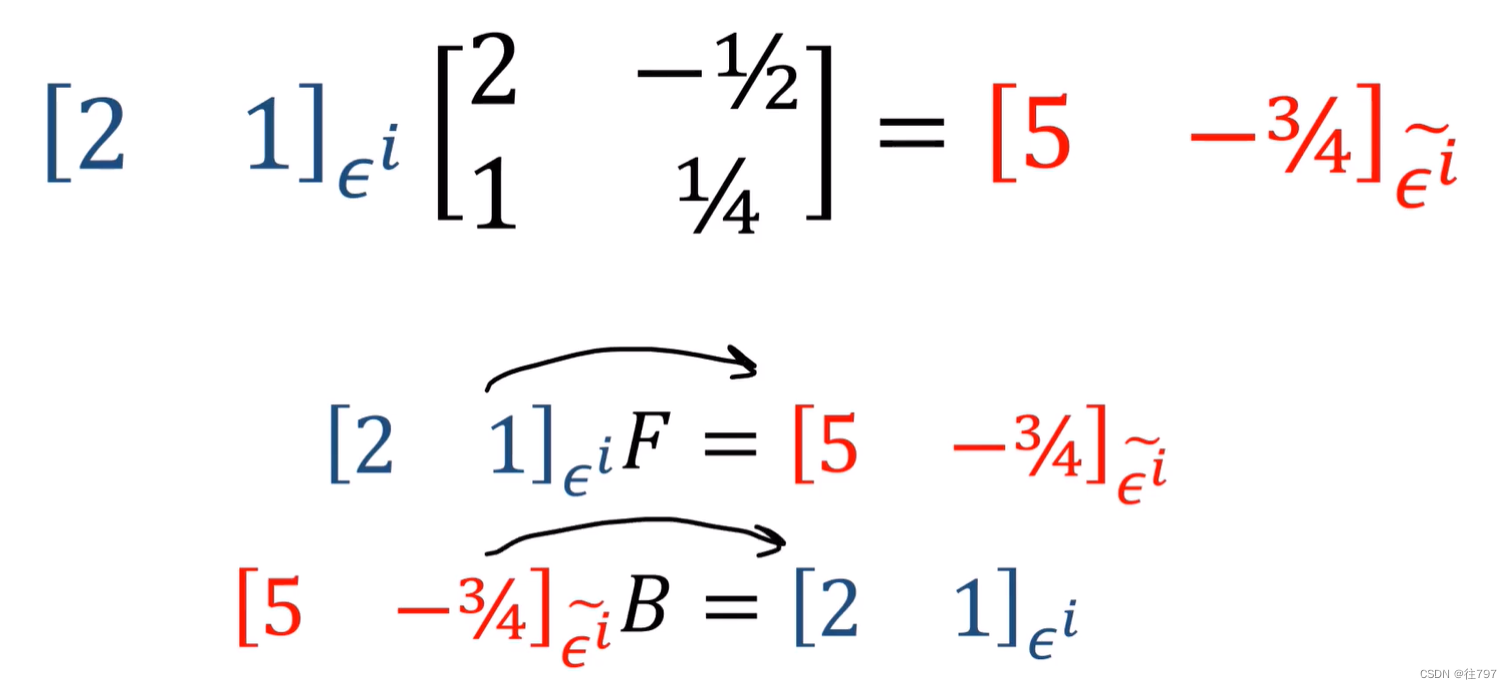
以上是向量的转换;
以下是基底的转换;
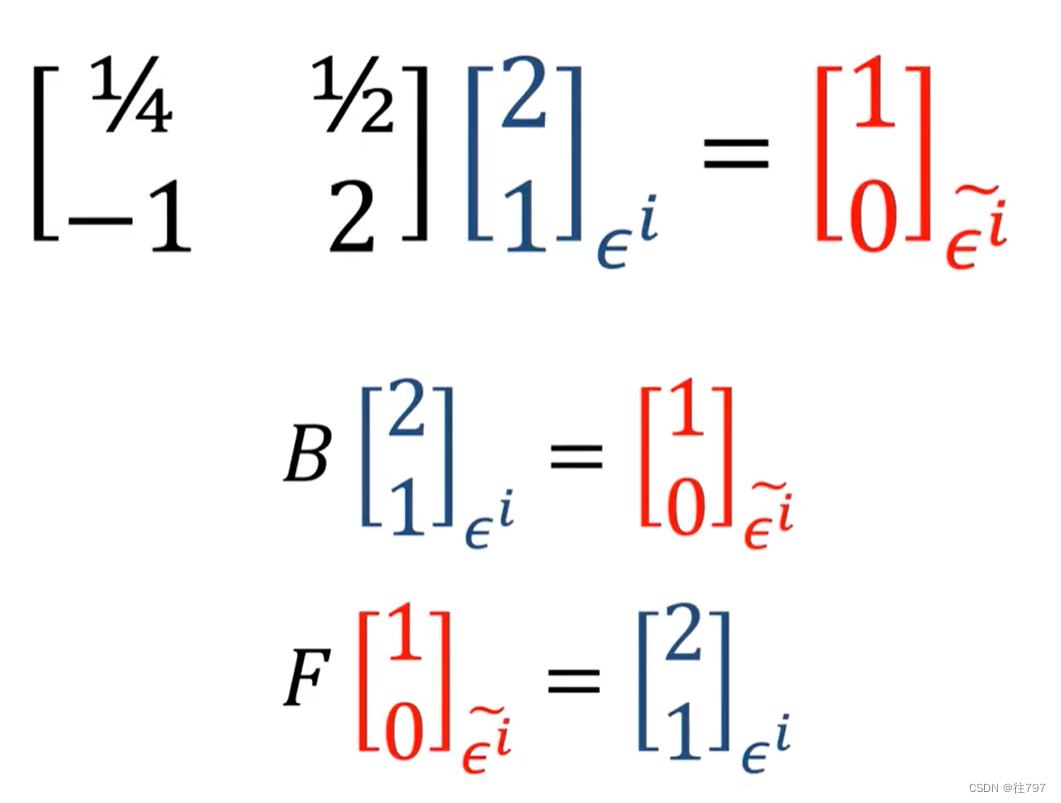
仔细观察,协向量中:基底的转换: 旧基到新基---用B,新基到旧基===用F;
这与向量的完全相反!
协向量中:某个协向量的转换:利用旧基到利用新基---用F,利用新基到利用旧基--用B
这与向量的完全相反!
这就是为什么不能只翻转列向量来获得行向量,--------这在正交基上有效,
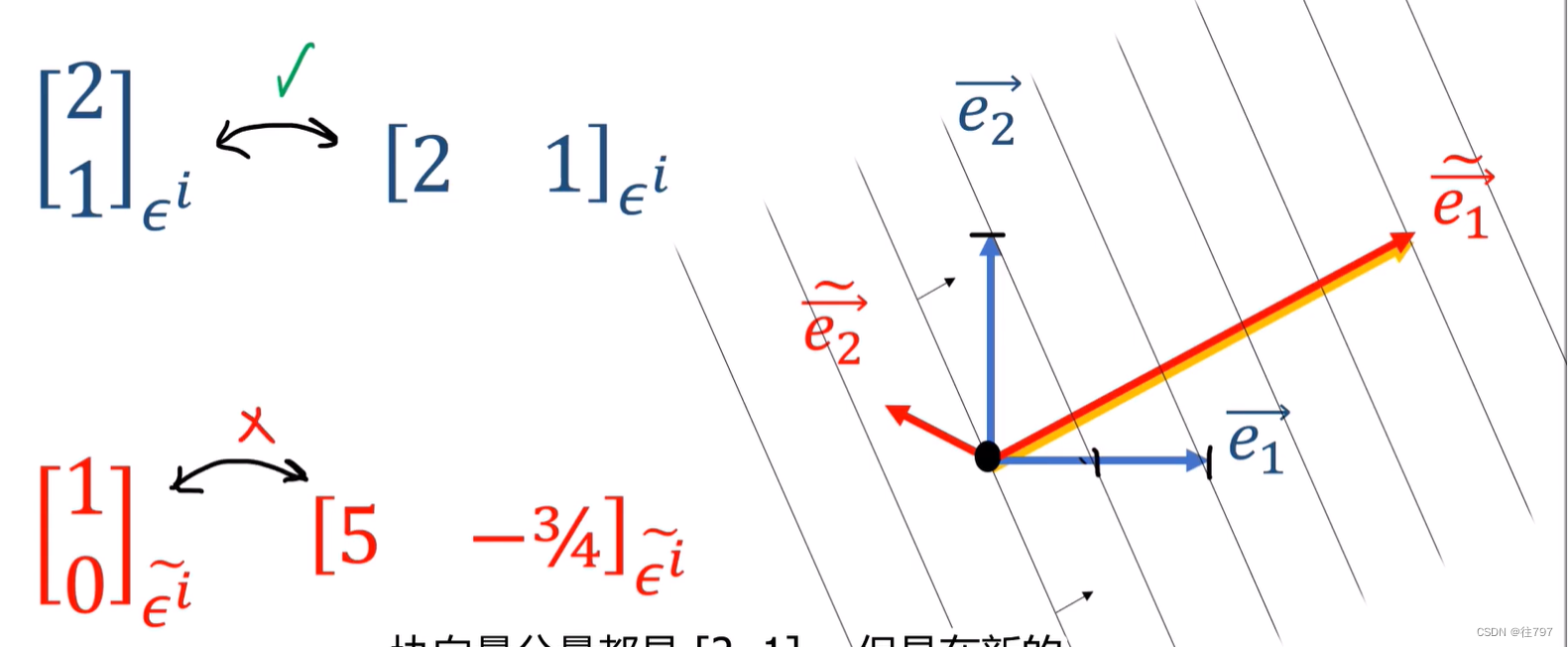
你看上图, 对于利用正交基, 协向量你把它从列向量转置成行向量,2,1仍是2,1;
但是,一旦不是正交基了, 【1;0】变为 【5,-3/4】明显不能靠转置来获得。
所以,向量分量是通过计算构建向量时使用了多少基向量来测量的,
但是协向量分量是通过计算 基向量 穿过的协向量线的数量来测量的。