目录

一、安全性算法

二、基础术语

三、对称加密与非对称加密

四、数字签名

五、 哈希算法

六、哈希算法碰撞与溢出处理

---

 

一、安全性算法

安全性算法的必要性：

  安全性算法的必要性是因为在现代数字化社会中，我们经常需要传输、存储和处理敏感的数据，如个人隐私信息、金融数据、商业机密等。这些数据如果未经过适当的保护，可能会被恶意攻击者获取、篡改或滥用。

安全性算法遵循以下四个特性

1. 保密性（Confidentiality）：确保只有授权者才能访问和查看数据，对非授权人员保持数据保密。

2. 完整性（Integrity）：确保数据在传输和存储过程中没有被篡改、损坏或破坏，保持数据的完整性和一致性。

3. 认证性（Authentication）：确认数据的来源和真实性，确保数据发送者和接收者的身份是真实的，并且数据没有被冒充或伪造。

4. 不可否认性（Non-Repudiation）：确保数据的发送者不能否认他/她发送过的数据，防止他/她在后期否认该数据的发送或者执行。

---

二、基础术语

概念	定义
明文	未经过加密处理的原始数据或信息。
密钥	用来进行加密和解密的一串字符或数字，只有持有相应密钥的人才能对加密数据进行解密。
密文	加密明文后的数据或信息。
私钥	用于非对称加密算法的一种密钥，只有私钥持有者才能进行解密。
公钥	用于非对称加密算法的一种密钥，公钥可以公开给任何人使用，但只有私钥持有者才能进行解密。
加密函数	一种算法，将明文和密钥作为输入，生成密文作为输出，实现对数据的保护。
解密函数	一种算法，将密文和密钥作为输入，生成明文作为输出，实现对加密数据的还原。

---

三、对称加密与非对称加密

1.对称加密

        对称加密是一种加密技术，使用相同的密钥（也称为对称密钥）进行加密和解密。在对称加密算法中，发送方使用密钥将明文转换为密文，接收方使用相同的密钥将密文转换回明文。

        对称加密的优点是加密和解密速度快，适用于大量数据的加密和解密操作。常见的对称加密算法有DES（数据加密标准）、AES（高级加密标准）等。

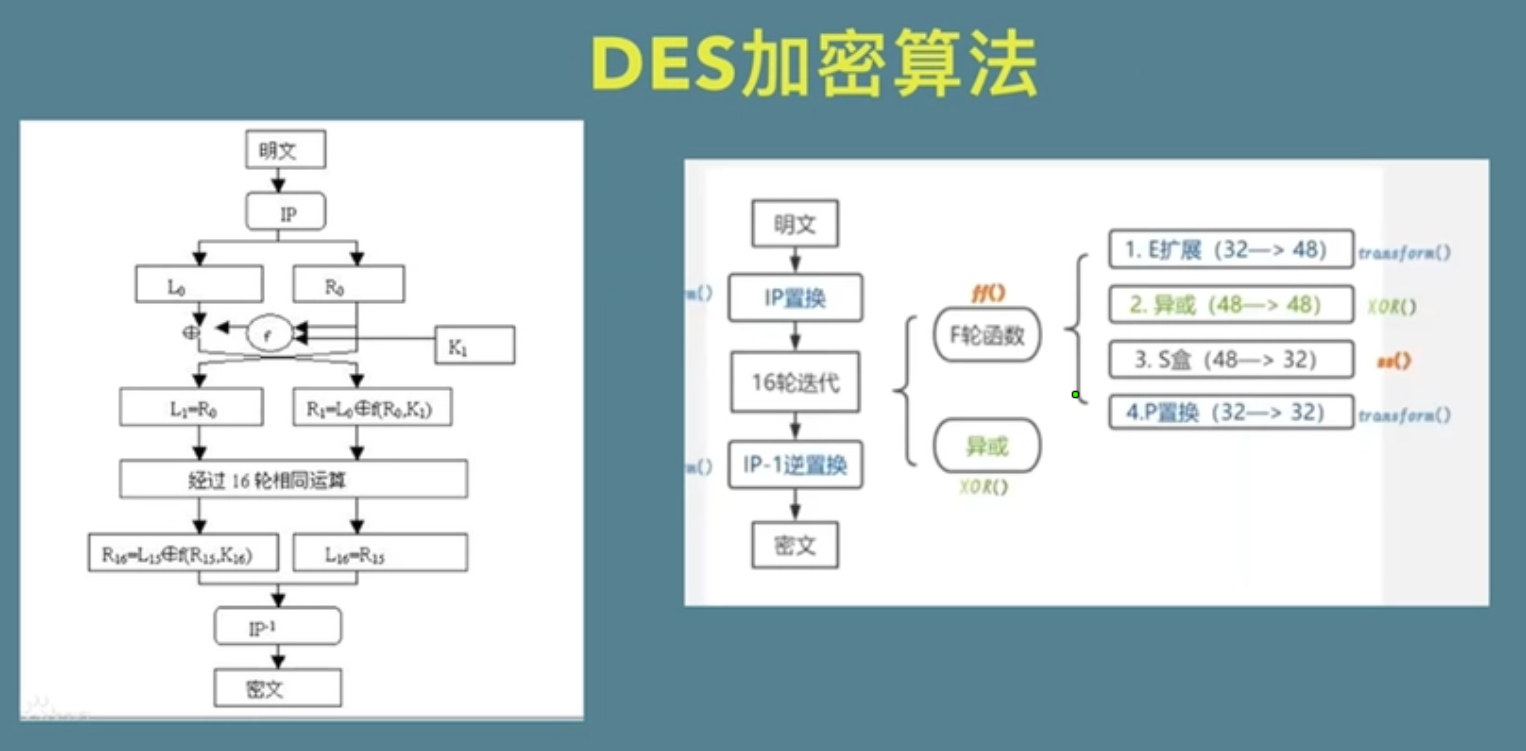
优点： 加密和解密速度快，适用于大量数据的加密和解密操作。常见的对称加密算法有DES（数据加密标准）、AES（高级加密标准）等。然而，对称加密存在一个问题，即如何安全地共享密钥。如果密钥在传输过程中被攻击者获取，那么加密的安全性就会被破坏。因此，在某些情况下，非对称加密算法更常被用于密钥的安全交换。

2.非对称加密

        非对称加密是一种加密技术，与对称加密算法不同，它使用一对密钥进行加密和解密操作。这对密钥包括公钥（public key）和私钥（private key）。公钥可以公开给其他人使用，而私钥则只能由密钥的所有者保管，不公开给他人。

        在非对称加密中，发送方使用接收方的公钥来加密数据，而接收方则使用自己的私钥来解密。相反，如果发送方要发送加密的信息给接收方，发送方可以使用自己的私钥进行签名，接收方使用发送方的公钥验证签名的有效性。这种加密和解密操作过程使用不同的密钥，因此被称为“非对称”。

常用非对称加密RSA

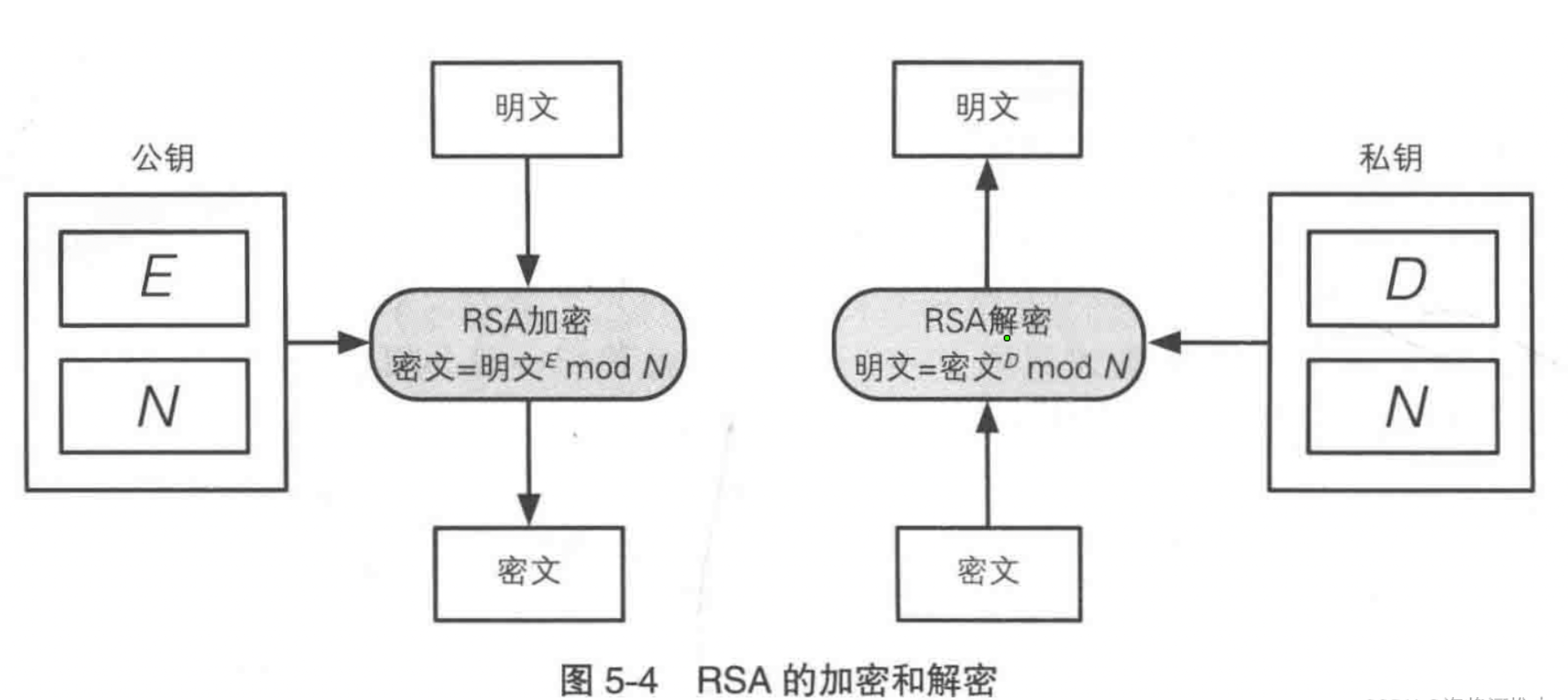
优点： 可以实现加密和解密的分离，并且可以安全地共享公钥。即使公钥被其他人获取，也无法通过公钥推导出私钥。常见的非对称加密算法有RSA（由Rivest、Shamir和Adleman发明）和Elliptic Curve Cryptography（椭圆曲线加密）等。

---

四、数字签名

1.数字签名概念

        数字签名是一种用于验证数据完整性、身份认证和防止数据篡改的加密技术。它常用于确保发送方的身份，以及确保数据在传输过程中没有被篡改或伪造。

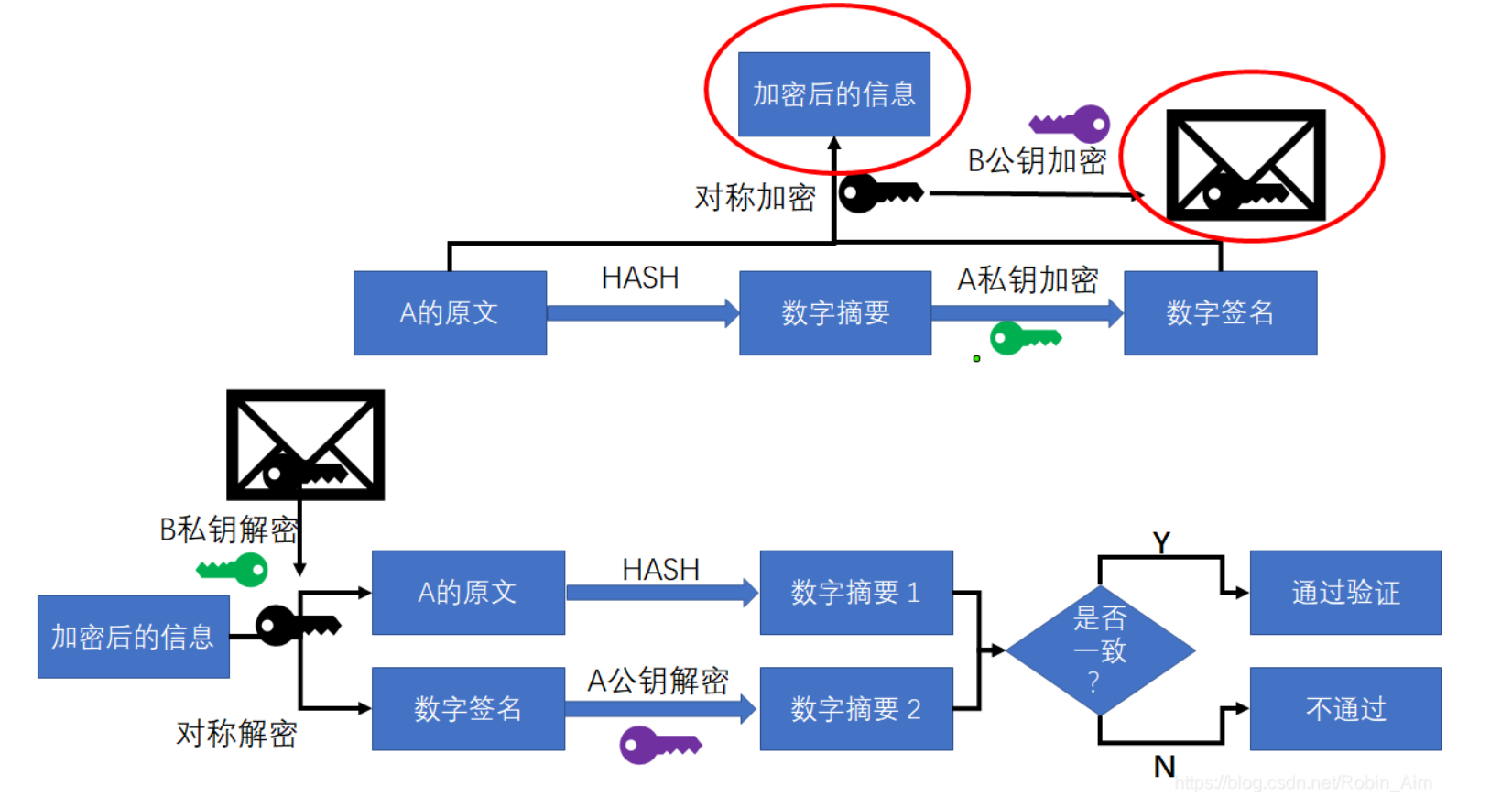
2.数字签名工作方式

        数字签名的工作方式是以公钥和哈希函数相互配合使用的，用户A先将明文的M以哈希函数计算出哈希值H，再用自己的私钥对哈希值H进行加密，加密后的内容和即为"数字签名"。最后将明文与数字签名一起发送给用户B。由于这个数字签名是由用户A的私钥进行加密的，且该私钥只有A才有，因此该数字签名可以代表A的身份。

---

五、 哈希算法

1.哈希算法是通过哈希函数计算一个键值对应的地址，进而建立哈希表，并依靠哈希函数查找各个键值存放在哈希表中的地址。查找速度与数据的多少无关，在没有碰撞和数据溢出的情况下即可查找成功，该方法还有保密性高的特点。

常见的哈希算法有除留余数法，平方取中法，折叠法和数字分析法

1.除留余数法

最简单的哈希函数是将数据除以一个某个常数后，取余数作为索引。

h(key) = key mod B

案例：在一个有13个位置的数组中，只是用7个地址，值分别是12,65,70,99,33,67,48。那么B就可以是13 。

案例代码：

public class javaDemo {
    public static void main(String[] args) {
        Map<Integer,Integer> map = new HashMap<>();
        int data[] = new int[]{12,65,70,99,33,67,48};
        //初始化哈希表
        for (int i=0;i<13;i++){
            map.put(i,null);
        }
        //除留余数
        for (int temp:data) {
            map.put((temp%13),temp);
        }
        System.out.println(map);
//注意：改代码只是展示除留余数法，碰撞问题将在后面进行修改
    }
}

注意：B虽然可以自己定义，但是尽量选择用质数（除了1和自身外没有其他正因数的数）

2.平方取中法

 平方取中法和除留余数法相当类似，就是先计算数据的平方，之后取中间的某段数字作为索引。

案例：
原始数据：12，65，70，99，33，67，51

平方后：144，4225，9801，1089，4489，2601

再通过取百位数或者十位数作为键值，取值后如下。

14，22，90，80，08，48，60

将上述7个数字对应原来的七个原始数据(12，65，70，99，33，67，51)

如果存放的空间为100地址空间

则正常进行数据映射如

f(14) = 12

f(22) = 65

.....

如果存放的空间为10地址空间，则需要对取值后的数进行压缩10倍，即14/10 = 1,22/10=2...

f(1) = 12

f(2) = 65

........

3.折叠法

        折叠法是将数据转换为一串数字后，先将这串数字拆成及部分，再把他们加起来，就可以计算出这个键值的桶地址（Bucket Address），例如，有一个数据转换成数字后为2365479125443.若以每四个数字为一个部分，则可以拆分成2365、4791、2544、3.将这4组数字加起来后即为索引值。

2365+4791+2544+3 = 9703 ->桶地址

        在折叠法中有两种做法。一种是向上例那样直接将每一部分相加所得的值作为其桶地址，这种做法成为“移动折叠法”。哈希法的设计原则之一是降低碰撞，如果希望降低碰撞，就可以将上述的数字中的技术为段或偶数位段反转后相加，以取得桶地址，这种改进后的做法成为“边界折叠法”

        还是以上面的数字为例，请看下列说明

情况一：将偶数位段反转

   2365（第一位的是奇数位，故不反转）

+1974（第二位的是偶数位，故要反转）

+ 2544（第三位的是奇数位，故不反转）

+ 3      （第四位的是偶数位，故要反转）

= 6886 ->桶地址

情况二：将奇数位段反转

   5632 （第一位的是奇数位，需要反转）

+ 4791（第二位的是偶数位，故不反转）

+ 4452（第三位的是奇数位，需要反转）

+ 3        （第四位的是偶数位，故不反转）

= 14878 -> 桶地址

4.数字分析法

数字分析法，通过分析数据，找取数据中数字重复率低的数字，将索引空间放在数据中重复率最低的位置，以此作为数据的索引。

---

六、哈希算法碰撞与溢出处理

碰撞与溢出

        哈希算法将输入数据映射到固定长度的哈希值。碰撞是指不同的输入数据最终得到相同的哈希值，而溢出则是指较大的输入数据映射到较小的输出空间中。这些问题的出现是由于哈希算法必须处理无限输入空间映射到有限输出空间的情况导致的。虽然设计者会尽力减少碰撞和溢出的概率，但在某些情况下仍无法完全避免。

1.线性探测法

线性探测算法：

public class javaDemo {
    public static void main(String[] args) {
        //假设地址空间为10,并且初始值为-1
        int index[] = new int[10];
        int num;
        int temp = num % index.length;
        
        while (true){
//            如果目标位置不存在数字则存入数据
            if (index[temp] == -1){
                index[temp] = num;
                break;
            }else {
                temp = (num+1) % index.length;
            }
        }
    }
}

 

---