---

二、曲面积分

2.2 对坐标的曲面积分（第二类曲面积分）

1. 问题产生 —— 流量

设 $\Sigma$ 为有侧曲面，流体的流速为 v → = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{v}=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} v ={P(x,y,z),Q(x,y,z),R(x,y,z)} ，单位时间内流过指定侧的曲面的流量 $\Phi$ 的计算思路（元素法）如下：

（1）任取 d S → = { d y d z , d z d x , d x d y } ⊂ Σ d\overrightarrow{S}=\{dydz,dzdx,dxdy\}\sub \varSigma dS ={dydz,dzdx,dxdy}⊂Σ ；

（2）$d\Phi =\overrightarrow{v}\cdot d\overrightarrow{S}=P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy$ ；

（3）$\Phi ={\iint }_{\Sigma }d\Phi ={\iint }_{\Sigma }P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy$ 。

2. 对坐标的曲面积分的定义（了解）

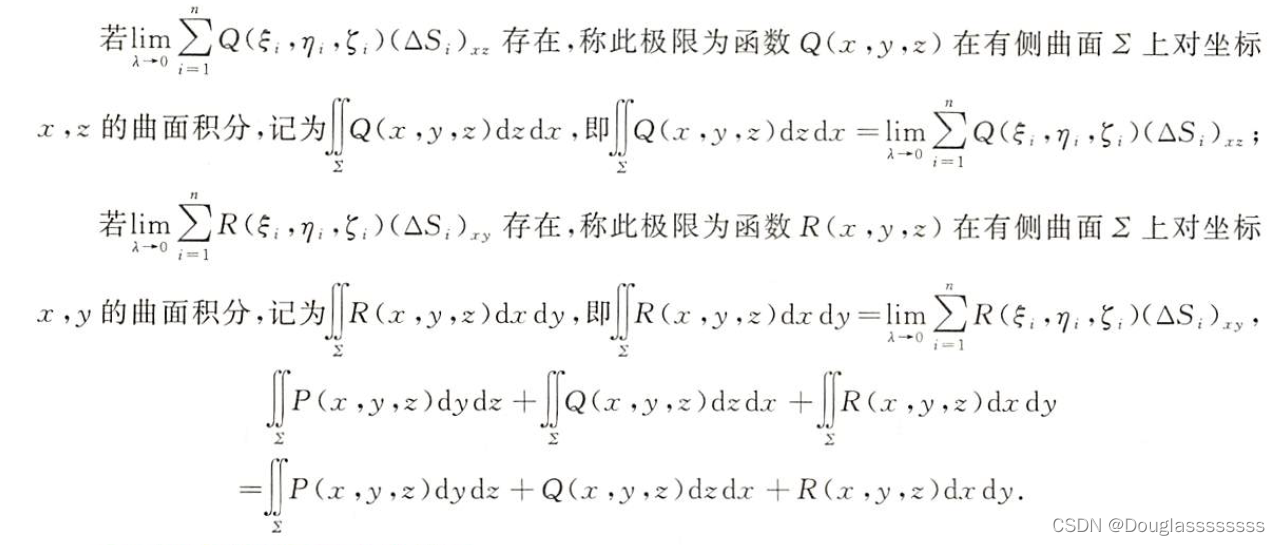
3. 对坐标的曲面积分的性质

这里说明几点特殊的，积分区域 $\Sigma$ 是有方向的，不同方向得到的积分结果互为相反数；对坐标的曲面积分也具有对称性，不过若关于 $xOy$ 面（变量 $z$ ），只需要判断 $R(x,y,z)$ 关于 $z$ 的奇偶性。需要注意的是，如果是奇函数，结果是两倍，偶函数才为零，这和前面是截然相反的！

4. 对坐标的曲面积分的计算法

（1） 二重积分法

对 ${\iint }_{\Sigma }R(x,y,z)dxdy$ 的计算：设 $\Sigma :z=u(x,y)$ ，其中 $(x,y)\in D_{xy}$ ，则 $${\iint }_{\Sigma }R(x,y,z)dxdy=\pm {\iint }_{\Sigma }R(x,y,u(x,y))dxdy.$$ 其中，若 $\Sigma$ 上一点的正侧法向量与 $z$ 轴的夹角为锐角，结果取正，否则取负。

其余两个情形可同理进行计算。

【例】设 $\Sigma :(x-1{)}^2+y^2+z^2=1$ ，取外侧，计算 ${\iint }_{\Sigma }{y}^{2}zdxdy$ 。

解： 易知，$\Sigma$ 表示的是一个球面，关于 $xOy$ 面对称，设上半球面为 ${\Sigma }_1$ ，有 $${\iint }_{\Sigma }{y}^{2}zdxdy=2{\iint }_{{\Sigma }_1}{y}^{2}zdxdy,$$ 令 ${\Sigma }_1:z=\sqrt{1-(x-1{)}^2-y^2},(x,y)\in D_{xy},D_{xy}:(x-1{)}^2+y^2\le 1$ ，则 $${\iint }_{\Sigma }{y}^{2}zdxdy=2{\iint }_{D_{xy}}{y}^2\sqrt{1-(x-1{)}^2-y^2}dxdy,$$ 令 $x=1+r\cos \theta ,y=r\sin \theta ,\theta \in [0,2\pi ],r\in [0,1]$ ，有 $$2{\iint }_{D_{xy}}{y}^2\sqrt{1-(x-1{)}^2-y^2}dxdy=2{\int }_0^{2\pi }{\sin }^2\theta d\theta {\int }_0^1{r}^3\sqrt{1-r^2}dr=\frac{4\pi }{15}.$$

（2）高斯公式

定理 —— 设 $\Omega$ 为几何体，$\Sigma$ 为 $\Omega$ 的外侧曲面，$P(x,y,z),Q(x,y,z),R(x,y,z)$ 在 $\Omega$ 上一阶连续可偏导，则 $\iint Pdydz+Qdzdx+Rdxdy={\iiint }_{\Omega }(\partial P/\partial x+\partial Q/\partial y+\partial R/\partial z)dv.$

【例】计算 $\iint x{z}^{2}dydz+(x^{2}y-z^3)dzdx+(2xy+y^{2}z)dxdy$ ，其中 $\Sigma$ 为 $z=\sqrt{1-x^2-y^2}$ 和 $z=0$ 所围区域表面外侧，如下图所示。

解： 由高斯公式可知：$\iint x{z}^{2}dydz+(x^{2}y-z^3)dzdx+(2xy+y^{2}z)dxdy={\iiint }_{\Omega }(z^2+x^2+y^2)dv={\int }_0^{2\pi }d\theta {\int }_0^{\pi /2}d\phi {\int }_0^1{r}^2{r}^2\sin \phi dr=2\pi /5.$

5. 两类曲面积分之间的关系

$$\iint Pdydz+Qdzdx+Rdxdy={\iint }_{\Sigma }(Pcos\alpha +Q\cos \beta +R\cos \gamma )dS.$$ 其中，$\cos \alpha ,\cos \beta ,\cos \gamma$ 为曲面 $\Sigma$ 正侧法向量的方向余弦。

【例】设 $f(x,y,z)$ 为连续函数，$\Sigma$ 为平面 $x-y+z-1=0$ 在第四卦限部分的上侧，计算 $${\iint }_{\Sigma }[f(x,y,z)+x]dydz+[2f(x,y,z)+y]dzdx+[f(x,y,z)+z]dxdy.$$ 解： 平面 $\Sigma$ 如下图所示：

曲面 $\Sigma$ 的法向量为 { 1 , − 1 , 1 } \{1,-1,1\} {1,−1,1} ，对应的方向余弦为 $\cos \alpha =1/\sqrt{3},\cos \beta =-1/\sqrt{3},\cos \gamma =1/\sqrt{3}$ ，则原积分可化为 $${\iint }_{\Sigma }\{[f(x,y,z)+x]/\sqrt{3}-[2f(x,y,z)+y]/\sqrt{3}+[f(x,y,z)+z]/\sqrt{3}\}dS.$$ 即 ${\iint }_{\Sigma }(x+z-y)/\sqrt{3}dS=S/\sqrt{3}=(1/2\times \sqrt{2}\times \sqrt{2}\times \sqrt{3}/2)/\sqrt{3}=1/2.$

---

三、场论初步

3.1 梯度、旋度、散度

设 $u=f(x,y,z)$ 可偏导，则 $u$ 的梯度为 g r a d   u = { ∂ f / ∂ x , ∂ f / ∂ y , ∂ f / ∂ z } \pmb{grad}\space u=\{\partial f/\partial x,\partial f/\partial y,\partial f/\partial z\} grad u={∂f/∂x,∂f/∂y,∂f/∂z} 。这个我们之前接触过，是函数在某点处增长最快的方向。

设向量场 A → = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A ={P(x,y,z),Q(x,y,z),R(x,y,z)} ，则 $\overrightarrow{A}$ 的旋度为 $$rot\overrightarrow{A}=\left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ P& Q& R\end{array}\right|.$$ 设向量场 A → = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A ={P(x,y,z),Q(x,y,z),R(x,y,z)} ，则 $\overrightarrow{A}$ 的散度为 $$div\overrightarrow{A}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}.$$

应该只会考梯度吧，我看其他两个连例题都没有。

3.2 通量与环流量

1. 通量

设 A → ( x , y , z ) = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A (x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)} 为向量场，其中 $P,Q,R$ 连续可偏导，$\Sigma$ 为有侧曲面，称 $\Phi ={\iint }_{\Sigma }Pdydz+Qdzdx+Rdxdy={\iint }_{\Sigma }\overrightarrow{A}\cdot \overrightarrow{n}dS$ 为向量场 $\overrightarrow{A}$ 指向指定侧的流过有侧曲面 $\Sigma$ 的通量（或流量），其中 $\overrightarrow{n}$ 为曲面 $\Sigma$ 的正侧单位法向量。

好像这个就是两类曲面积分之间的关系 O.O

2. 环流量

设 A → ( x , y , z ) = { P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) } \overrightarrow{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\} A (x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)} 为向量场，其中 $P,Q,R$ 连续可偏导，$L$ 为有向闭曲线，称 $${\oint }_{L}Pdx+Qdy+Rdz={\oint }_L\overrightarrow{A}\cdot d\overrightarrow{s}.$$ 为向量场 $\overrightarrow{A}(x,y,z)$ 沿有向闭曲线 $L$ 的环流量。

---

写在最后

曲面积分的学习是痛苦的，当然主要还是因为前面的二重、三重、空间解析几何不扎实，不过也顺利处理掉了。

那高等数学理论部分到此就全部结束了，一个漫长的过程，也是三门中分值最大的一部分。剩下的时间里就好好对它进行总结和实践吧。