目录
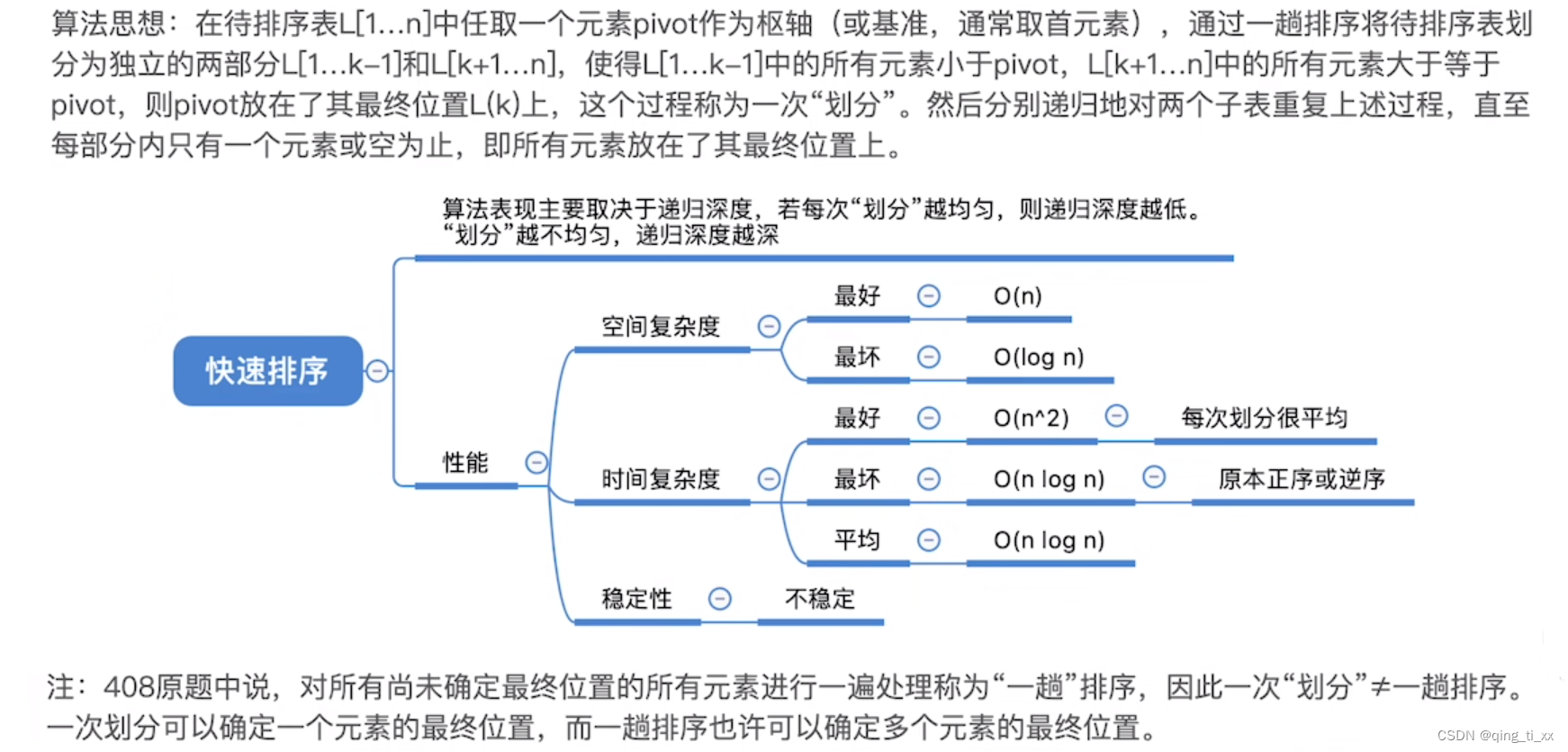
一、算法思想
二、例子
三、代码实现
四、验证
五、算法效率分析
1、时间复杂度
编辑
2、空间复杂度
3、小结
4、优化思路
5、稳定性
六、总结
一、算法思想
首先,选取一个数作为序列的基准数,分别定义序列的第一个数和最后一个数为low和high,让它们与基准数进行比较,如果low小于基准数,则low指针右移,反之将low指针所指元素移动到high指针所指的地方,high指针同理,以形成左边的序列都比基准数小,右边的序列都比基准数大。
二、例子
1、我们将此序列使用快速排序进行升序排序
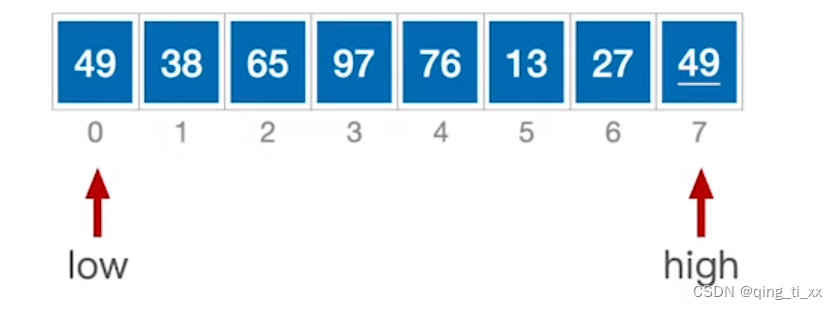 、2、选取49作为基准数,并将其存入缓存变量
、2、选取49作为基准数,并将其存入缓存变量
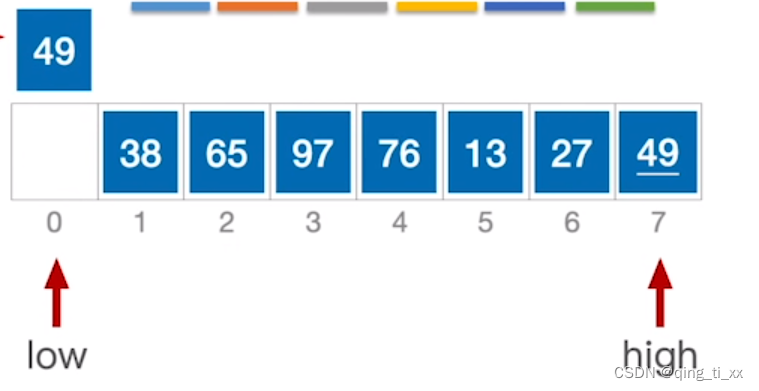
3、左移high指针,让27与基准数49进行比较,27比49小,则把27移动到low所指的位置

4、此时high指针为空,我们切换到low指针进行比较,让27与49比较,发现它小于49,所以low指针右移,38同理,当移动到65时,发现65大于49,所以将65放在high指针处

5、此时low指针处为空,于是我们切换到high指针,将high指针右移,让它与13比较,将13移动到low指针处

6、切换到low指针,将low右移,97比49大,所以97移动到high指针处
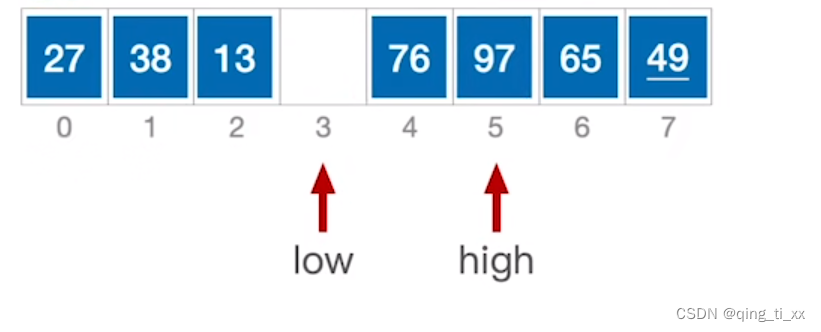
7、右移high,直到与low相遇,此时我们得到了基准数49应该存放的位置为3

8、于是我们将序列划分为了两个部分

9、然后我们再次对划分后的两部分分别取基准数27和76,再次进行划分
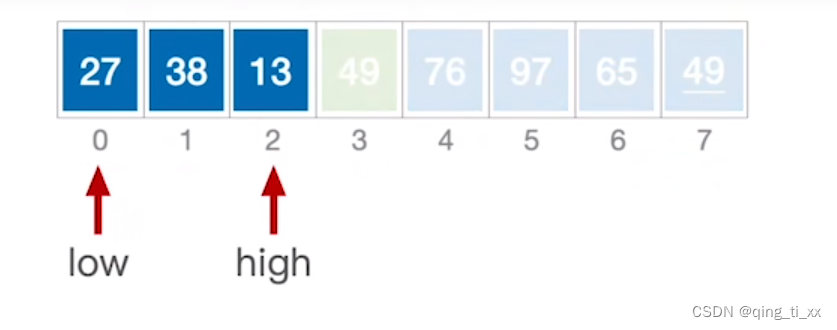

10、最终得到
三、代码实现
#include "bits/stdc++.h"
using namespace std;
int Partition(int a[],int low,int high){//划分函数
int pivot = a[low];//把第一个数作为基准数
while(low<high){
while (low<high && a[high]>=pivot)--high;//从右边开始,找到比基准数小的数
a[low] = a[high];//放到左边
while (low<high && a[low]<=pivot)++low;//从左边开始,找到比基准数大的数
a[high] = a[low];//放到右边
}
a[low] = pivot;//当把所有数划分为两边后,也就找到了基准数的位置,将基准数插入中间
return low;//返回划分位置的下标
}
void QuickSort(int a[],int low,int high){
if (low<high){//当符合排序条件时
int pivot = Partition(a,low,high);//将序列划分
QuickSort(a,low,pivot-1);//对左半子序列进行递归排序
QuickSort(a,pivot+1,high);//对右半子序列进行递归排序
}
}
int main(){
int count,arr[10];
scanf("%d",&count);//输入数组长度
for (int i = 0; i < count; ++i) {
scanf("%d",&arr[i]);//输入数组
}
QuickSort(arr,0,count-1);//调用排序函数
for (int i = 0; i < count; ++i) {
printf("%d ",arr[i]);//输出数组
}
return 0;
}四、验证

五、算法效率分析
1、时间复杂度
2、空间复杂度

3、小结
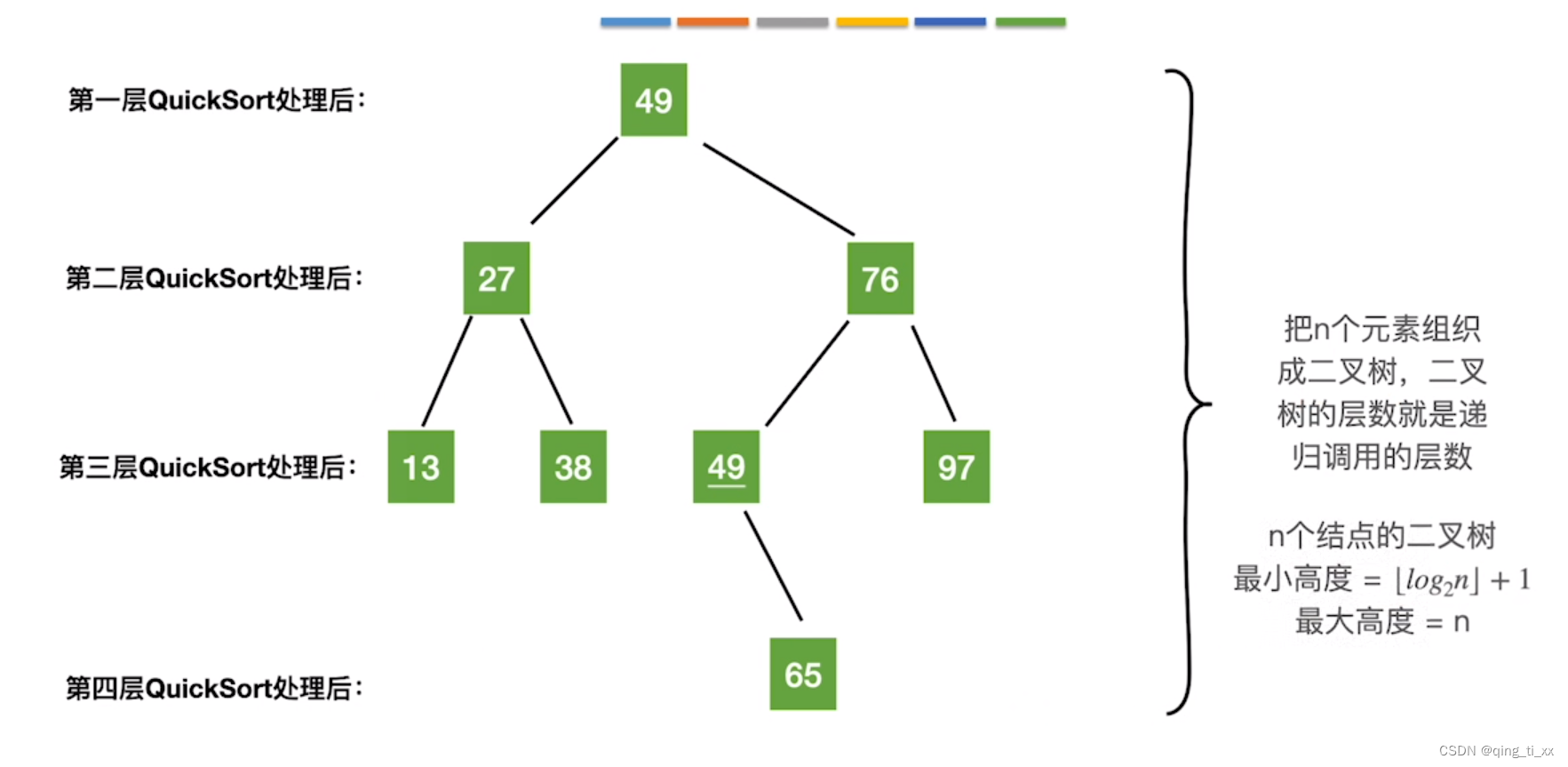
最坏的情况是序列本身就是顺序或逆序的

4、优化思路

5、稳定性
不稳定
六、总结