面试高频手撕算法 - 01背包系列

1. 前言

为什么要专门去搞一下这个背包问题呢 ? 因为作者已经在两场面试中吃了这个亏, 尤其是在面深信服的测开岗的时候, 一面的难度适中, 加上面试官也没为难我, 侥幸让我过了. (以下是一面问题)

二面的时候, 主要问了项目和手撕算法. 当时项目个人觉得面的还不错, 因为本人是双非二本的学生, 面试官对我的要求也不会太高. 面完项目后, 就到了手撕算法环节, 我当时觉得: 测开岗的手撕算法应该不会太难, 搞定牛客 Top101, 剑指 offer, 应该没什么大的问题.. 结果面试官上来就是一道经典 01 背包, 虽然现在我能做的很好, 但是当时只写过这道题的代码, 而且有段时间了, 也并没有好好地去理解这个思想, 所以连伪代码都没有写出来, 然后第二道也是动态规划相关的, 我只提供暴了力做法, 写出这代码我自己都笑了, 最终的结果可想而知了.....

俗话说: "在哪里跌倒, 在哪里爬起~" , 接下来好好研究一下背包系列的问题, 该如何解决.

---- 这篇文章主要讲 01 背包，下篇文章再讲完全背包和二维费用的背包问题 ----

2. 什么是 01 背包，什么是完全背包

此处只讲解 01 背包、完全背包、以及二维费用的背包问题，毕竟是面试，搞定这些基本上差不多了。

【定义】首先什么是背包问题 ?

背包问题的本质：解决有限制条件下的 " 组合 " 问题！

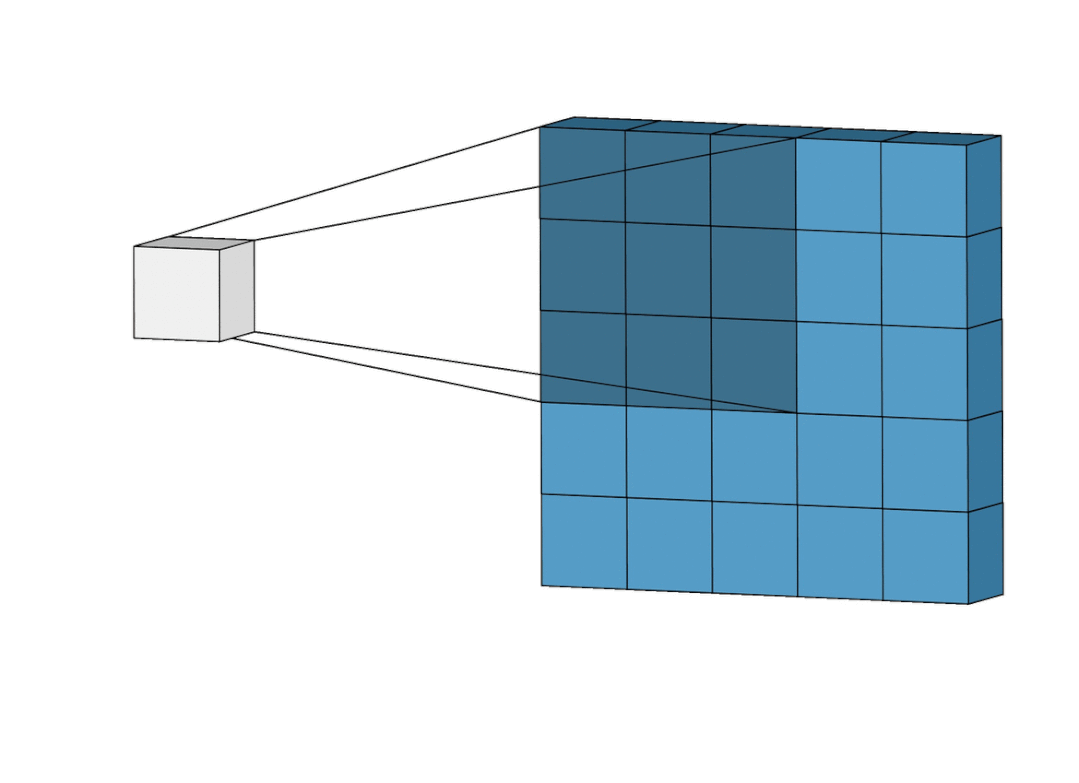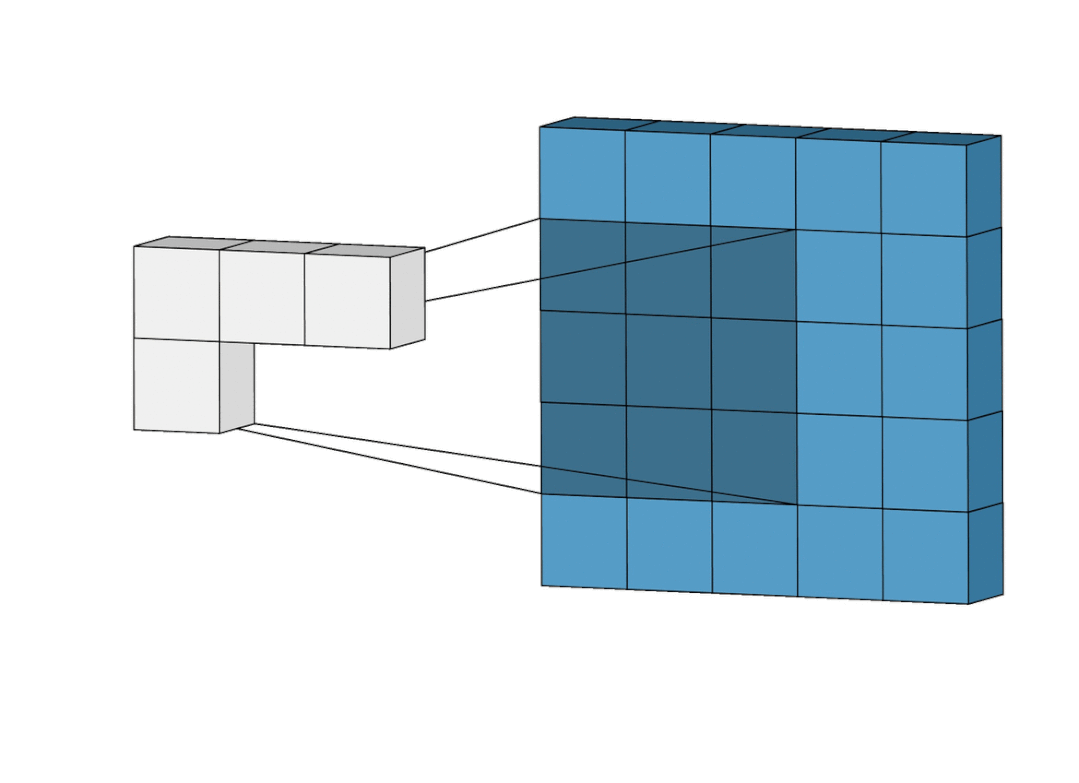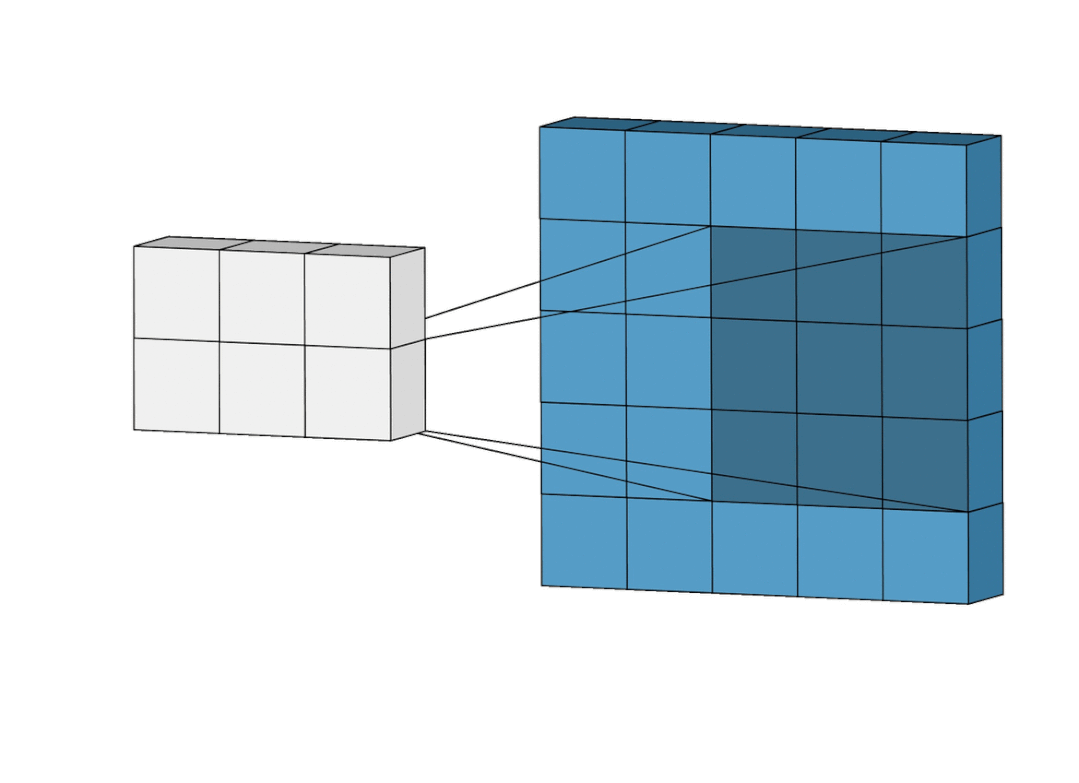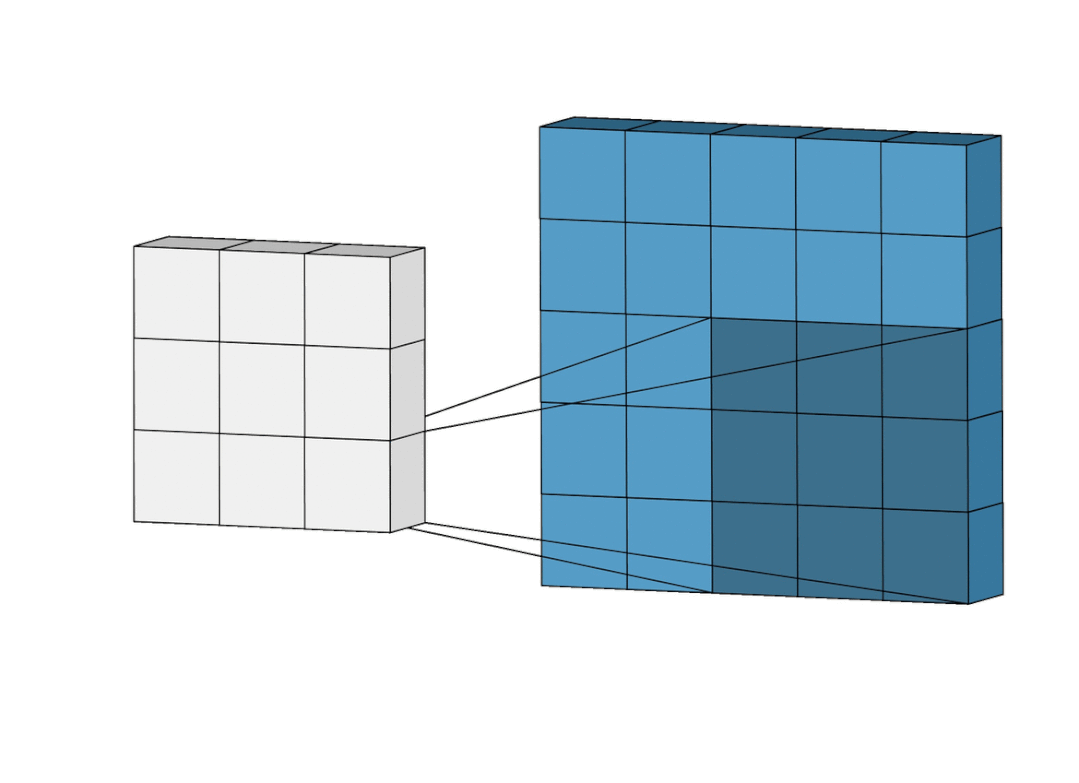
什么是 01 背包，什么是完全背包，以下面这幅图为例：

问题：在不超过背包体积的前提下，从这一堆物品中任意挑选某些物品，使得背包中的价值最大.

【01 背包】：每种物品只有一个，不能多次挑选.

01 背包中又可以分为必须装满和不用装满的两种情况.

【完全背包】：每种物品有无限个，可以多次挑选.

完全背包中又可以分为必须装满和不用装满的两种情况.

3. 01 背包

3.1 【模板】01背包

【题目链接】【模板】01背包_牛客题霸_牛客网你有一个背包，最多能容纳的体积是V。现在有n个物品，第i个物品的体积为 ,。题目来自【牛客题霸】https://www.nowcoder.com/practice/fd55637d3f24484e96dad9e992d3f62e?tpId=230&&tqId=38964&sourceUrl=https%3A%2F%2Fwww.nowcoder.com%2Fexam%2Foj

【题目描述】

你有一个背包，最多能容纳的体积是V。
现在有 n 个物品，第 i 个物品的体积为 vi,价值为 wi

（1）求这个背包至多能装多大价值的物品？
（2）若背包恰好装满，求至多能装多大价值的物品？

第一问：【算法原理】

再做动态规划系列问题的时候，无非就是这几大步骤：

① 状态定义

② 推导状态转移方程

③ 初始化 dp 表

④ 填表顺序

⑤ 返回值

1. 状态定义

背包问题本质上还是一个线性 dp, 所以状态的定义根据线性 dp 的经验:

状态定义: dp[i] 表示从前 i 个物品中挑选, 所有选法, 能挑选出来的最大价值 (试错)

但是这样定义状态之后, 发现推不出来, 因为不知道体积, 所以需要定义一个二维的 dp.

状态定义:dp[i][j]表示从前 i 个物品中挑选,总体积不超过 j,所有选法中,能挑选出来的最大价值

2. 推导状态转移方程

根据最后一个位置的状况, 分情况讨论:

所以最终的状态转移方程就是取两种情况的最大值即可:

// 满足 j >= v[i]
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);

当然这个状态转移方程可能还需要处理下标映射关系, 后续注意对应的代码即可.

3. 初始化 dp 表

为了方便代码进行 dp 的一个过程, 我们都会根据情况给 dp 表多加一行, 一列.

由于使用到前面的列的时候, 会进行判断, 所以初始化的时候, 可以不用初始化列, 只需要初始化行.

当只有 0 个商品的时候，想要体积不超过 0，1，2，3..... 最大价值肯定都是 0 了.

4. 填表顺序

从状态转移方程来分析，dp[i] 会使用到上一行，以及前面的列，所以填表顺序从上往下填即可.

5. 返回值

从状态表示：从前 i 个物品中挑选，总体积不超过 j 的最大价值，再结合题目要求，

得出最终的状态：从前 n 个物品中挑选，总体积不超过 V 的最大价值，所以返回 dp[n][V] 即可.

第一问：【编写关键代码】

/**
 * (1)求这个背包至多能装多大价值的物品？
 * @param v 每个商品所对应的体积
 * @param w 每个商品所对应的价值
 * @param V 背包体积
 * @param n 商品数量
 * @return
 */
public static int getMaxVlaue(int[] v, int[] w, int V, int n) {
    int[][] dp = new int[n + 1][V + 1];
    // 从前 i 个商品中挑选,总体积不超过 j,最大价值是多少
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= V; ++j) {
            // 不挑选 i 商品
            dp[i][j] = dp[i - 1][j];
            // 挑选 i 商品时,要考虑是否能装得下
            if(j - v[i] >= 0) {
                dp[i][j] = Math.max(dp[i][j],dp[i - 1][j - v[i]] + w[i]);
            }
        }
    }
    return dp[n][V];
}

此处先理解最基础的代码，等看完第二问，再统一做空间优化.

第二问：【算法原理】

1. 状态定义

有了前面的经验，接下来就直接定义状态了.

状态定义:dp[i][j]表示从前 i 个物品中挑选,总体积正好为 j,所有选法中,能挑选出来的最大价值

2. 推导状态转移方程

此处的状态转移方程和第一问几乎一模一样，只需要处理一些细节：

【细节】

dp[i - 1][j] 可能不存在，因为可能会有这样的情况，我怎么挑选商品，都不可能正好凑成体积为 j，所以可以使用 dp[i][j] = -1 来处理这种情况. （为什么不使用 0 来处理，因为我们在初始化 dp 表的时候，多加了一行，一列，而里面就有 0 值，这样容易误解.）

3. 初始化 dp 表

此处初始化 dp 表的时候，就不能给第一行设为 0 了，而是设为 -1.

因为没有商品的时候，不可能凑出体积为 1，2，3 的情况.

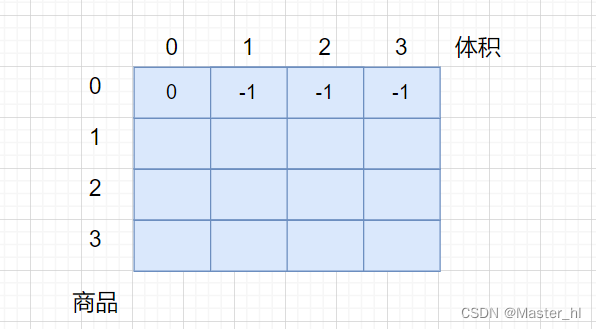
4. 填表顺序

填表顺序依旧从上往下即可.

5. 返回值

dp[n][V]

第二问：【编写关键代码】

/**
 * (2)若背包恰好装满，求至多能装多大价值的物品？
 * @param v 每个商品所对应的体积
 * @param w 每个商品所对应的价值
 * @param V 背包体积
 * @param n 商品数量
 * @return
 */
public static int getMaxVlaue(int[] v, int[] w, int V, int n) {
    int[][] dp = new int[n + 1][V + 1];
    // 状态定义：从前 i 个商品中挑选,体积恰好等于 j,最大价值为多少

    // 体积不能正好等于 j 的,统统初始化为 -1
    for(int j = 1; j <= V; ++j) dp[0][j] = -1;
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= V; ++j) {
            // 不选 i
            dp[i][j] = dp[i - 1][j];
            // 选 i，细节处理
            if(j - v[i] >= 0 && dp[i - 1][j - v[i]] != -1) {
                dp[i][j] = Math.max(dp[i][j],dp[i - 1][j - v[i]] + w[i]);
            }
        }
    }
    return dp[n][V];
}

【空间优化】

利用滚动数组做空间上的优化
直接在原始代码上稍加修改即可

从状态转移方程：dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - v[i] + w[i]]) 来看，每一个 dp[i][j] 都只会用到上一行的当前列和上一行的前面某列的值，所以上一行之前的行都是多余的空间，于是可以使用滚动数组进行优化.

原始的滚动数组是创建两个数组，每次保存上一行的所有值，当前行依赖上一行的值，填完一行，数组就往下滚一行：

但是没必要搞两个数组，我们仅需从后往前填表，就能完成滚动数组的效果，因为从后往前填表，它前面的状态就是上一行的状态。

第一问：空间优化后的代码

public static int getMaxVlaue(int[] v, int[] w, int V, int n) {
    int[] dp = new int[V + 1];
    // 状态定义：从前 i 个商品中挑选,总体积不超过 j,最大价值是多少
    for(int i = 1; i <= n; ++i) {
        // 从后往前填表
        for(int j = V; j >= v[i]; --j) {
            // 省去条件判断，直接放在循环里面
            dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);
        }
    }
    return dp[V];
}

第二问：空间优化后的代码

public static int getMaxVlaue(int[] v, int[] w, int V, int n) {
    int[] dp = new int[V + 1];
    // 从前 i 个商品中挑选,体积恰好等于 j,最大价值为多少
    for(int j = 1; j <= V; ++j) dp[j] = -1; // 初始化
    for(int i = 1; i <= n; ++i) {
        for(int j = V; j >= v[i]; --j) {
            if(dp[j - v[i]] != -1) {
                dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);
            }
        }
    }
    // 可能不存在正好装满的情况
    return dp[V] == -1 ? 0 : dp[V];
}

第二问的空间，我在 leetcode 题解里面也看到有不需要做 if 条件判断的，他们是怎么做到的呢？

是这样子的：

当背包问题的问法，涉及到最大，最小的结果，而且务必要恰好装满背包时，这个时候可以根据实际情况给第一行所有值初始化为 0x3f3f3f3f。

当求最大价值的时候，就初始化为 -0x3f3f3f3f，因为这个值足够小，那么在求 max 的时候，永远不会取到
当求最小价值的时候，就初始化为 0x3f3f3f3f，因为这个值足够大，那么在求 min 的时候，也永远不会取到

这样处理完之后，返回值也是需要处理的，具体代码如图下：

public static int getMaxVlaue(int[] v, int[] w, int V, int n) {
    int[] dp = new int[V + 1];
    // 从前 i 个商品中挑选,体积恰好等于 j,最大价值为多少
    for(int j = 1; j <= V; ++j) dp[j] = -0x3f3f3f3f; // 初始化
    for(int i = 1; i <= n; ++i) {
        for(int j = V; j >= v[i]; --j) {
            dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]);
        }
    }
    // 可能不存在正好装满的情况
    return dp[V] < 0 ? 0 : dp[V];
}

有了这两道 01 背包的基础之后，后面的 01 背包相关的题目，可以先自己尝试去做，在看答案之前，自己能做出来，记忆还是非常深刻的.

3.2 分割等和子集

【题目链接】

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台备战技术面试？力扣提供海量技术面试资源，帮助你高效提升编程技能，轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/partition-equal-subset-sum/【题目描述】

给你一个只包含正整数的非空数组 nums 。请你判断
是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

【算法原理】

这道题如果上来就将数组拆分成两部分，你会发现会很难做，所以再做这道题之前，我们可以把题目意思转化一下：

从上图来看，我们可以发现，两堆数据的总和始终都等于 sum / 2

于是这个问题就转换为了：从 n 个数中挑选一些数，让这些数的和等于 sum / 2.

这样来看，这就是一个 01 背包问题.

1. 状态定义

状态定义：dp[i][j]表示从前 i 个数中选，能否凑成 j 这个数 [true or false]

2. 推导状态转移方程

根据最后一个位置的状况, 分情况讨论:

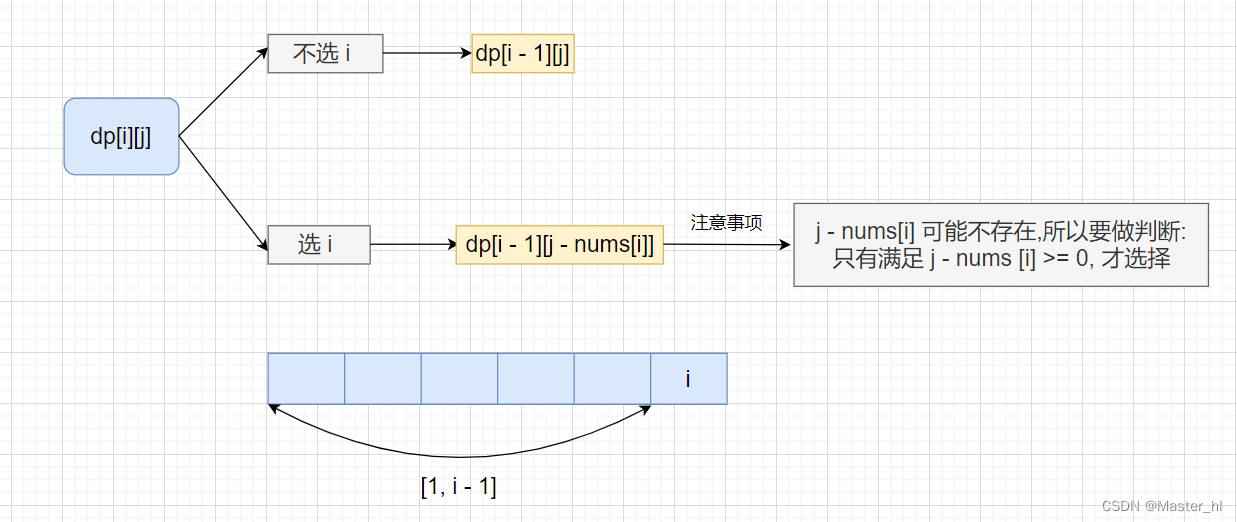
题目要求找到即可，所以最终的状态转移方程为：

dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]

3. 编写代码

有了状态转移方程，后续的初始化，填表顺序，以及返回值都很容易分析出来了，可以先自己分析再看代码.

初始化过程模棱两可的时候务必要要画图去理解！

public boolean canPartition(int[] nums) {
    int n = nums.length;
    int sum = 0;
    // 计算总和
    for(int i = 0; i < n; ++i) sum += nums[i];
    // 总和为奇数，就不可能分为相等的两堆
    if(sum % 2 != 0) return false;

    int aim = sum / 2;
    // 状态定义：从前 i 个数中挑选, 能否凑成 j 这个数
    boolean[][] dp = new boolean[n + 1][aim + 1];
    // 初始化
    for(int i = 0; i <= n; ++i) dp[i][0] = true;
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= aim; ++j) {
            // 第 i 数个不选
            dp[i][j] = dp[i - 1][j];
            // 第 i 数选
            if(j - nums[i - 1] >= 0) {
                dp[i][j] = dp[i][j] || dp[i - 1][j - nums[i - 1]];
            }
        }
    }
    return dp[n][aim];
}

4. 空间优化

public boolean canPartition(int[] nums) {
    int n = nums.length;
    int sum = 0;
    // 计算总和
    for(int i = 0; i < n; ++i) sum += nums[i];
    // 总和为奇数，就不可能分为相等的两堆
    if(sum % 2 != 0) return false;

    int aim = sum / 2;
    // 状态定义：从前 i 个数中挑选, 能否凑成 j 这个数
    boolean[] dp = new boolean[aim + 1];
    // 初始化
    dp[0] = true;
    for(int i = 1; i <= n; ++i) {
        for(int j = aim; j >= nums[i - 1]; --j) {
            dp[j] = dp[j] || dp[j - nums[i - 1]];
        }
    }
    return dp[aim];
}

3.3 分割等和子集

【题目链接】

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台备战技术面试？力扣提供海量技术面试资源，帮助你高效提升编程技能，轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/target-sum/【题目描述】

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联
起所有整数，可以构造一个表达式 ：

  例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，
在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

【算法原理】

这道题如果上来就用动态规划，状态定义是非常难定义的，状态转移方程更难推导，所以尝试将问题转换一下.

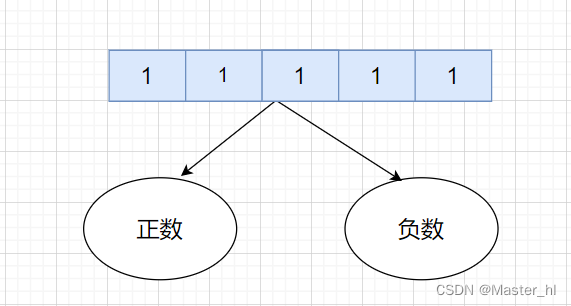
当我们给数组中的数据加上正负号的时候，就被分为了两堆数，一类正数，一类负数，假设所有正数的和为 a，所有负数的和的绝对值为 b，原始数组和为 sum，此时能得到两个公式：

a + b = sum
a - b = target

进而求出 a = (sum + target) / 2

所以这道题就转换为了：从 n 个数中挑选，和正好等于 target，一共有多少种选法.

这不就是 01 背包问题吗~

1. 状态定义

状态定义: 从前 i 个数中选,总和正好等于 j,一共有多少种选法

2.推导状态转移方程

注意事项：不选 i 的情况，一定不能写成 dp[i - 1][j] + 1，因为此处求得是选法有多少种，所以只需要将 i 位置拼接在末尾即可，不是多的选法，可以结合状态定义来理解.

最终的状态转移方程：

dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]

3. 编写代码

初始化过程模棱两可的时候务必要要画图去理解！

public int findTargetSumWays(int[] nums, int target) {
    int n = nums.length;
    int sum = 0;
    // 计算原始数组总和
    for(int i = 0; i < n; ++i) sum += nums[i];
    // 因为公式为 (sum + target) / 2, 所以此处一定要能够整除 2
    int a = sum + target;
    if(a % 2 != 0 || a < 0) return 0;

    int aim = (sum + target) / 2;
    int[][] dp = new int[n + 1][aim + 1];
    // 状态定义: 从前 i 个数中选,总和正好等于 j,一共有多少种选法

    dp[0][0] = 1; // 初始化
    for(int i = 1; i <= n; ++i) {
        for(int j = 0; j <= aim; ++j) {
            dp[i][j] = dp[i - 1][j]; // 不选 i
            if(j - nums[i - 1] >= 0) {
                dp[i][j] += dp[i - 1][j - nums[i - 1]]; // 选 i
            }
        }
    }
    return dp[n][aim];
}

4. 空间优化

public int findTargetSumWays(int[] nums, int target) {
    int n = nums.length;
    int sum = 0;
    // 计算原始数组总和
    for(int i = 0; i < n; ++i) sum += nums[i];
    // 因为公式为 (sum + target) / 2, 所以此处一定要能够整除 2
    int a = sum + target;
    if(a % 2 != 0 || a < 0) return 0;

    int aim = (sum + target) / 2;
    int[] dp = new int[aim + 1];
    // 状态定义: 从前 i 个数中选,总和正好等于 j,一共有多少种选法

    dp[0] = 1; // 初始化
    for(int i = 1; i <= n; ++i) {
        for(int j = aim; j >= nums[i - 1]; --j) {
            dp[j] += dp[j - nums[i - 1]];
        }
    }
    return dp[aim];
}

3.4 最后一块石头的重量

【题目链接】

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台备战技术面试？力扣提供海量技术面试资源，帮助你高效提升编程技能，轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/last-stone-weight-ii/【题目描述】

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y
那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎;
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

【算法原理】

这道题，如果上来直接用动态规划来写，状态是很难定义的，所以也是需要尝试去转换一下问题

假如有 5 个石头，重量分别为 a，b，c，d，e，碎石头的过程如下：

这样一写出来，就和目标和有点像了，但是这题求的是最小重量，但是大致可以往思考目标和的那个方向去靠：

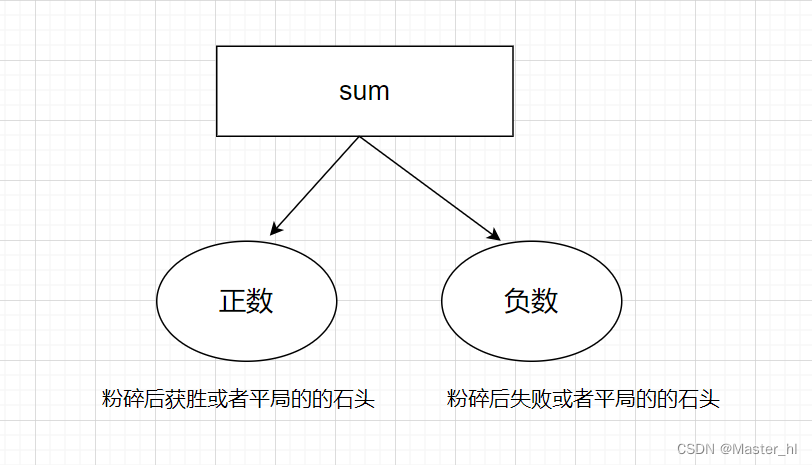
如果这样理解，那么我们可以把正数这一边的石子的加和设为 a，负数这一边的石子的加和设为 b，并且 a > b（如果不满足就调换一下），所以题目的要求就转换为了求 a - b 的最小值，那么 a - b 的最小值就是当 a 最接近 sum / 2 的时候，于是题目就变成了：

"从 n 个石子里选一些石子，使得石子的重量和尽可接近 sum / 2 "，求出 a 的值，那么 b 的值也可也得出来，那么最终的石头的重量，就拿 a，b 做差即可.

1. 状态定义

状态定义：从前 i 个石头中挑选，重量之和不超过 j，此时重量的最大和

2. 推导状态转移方程

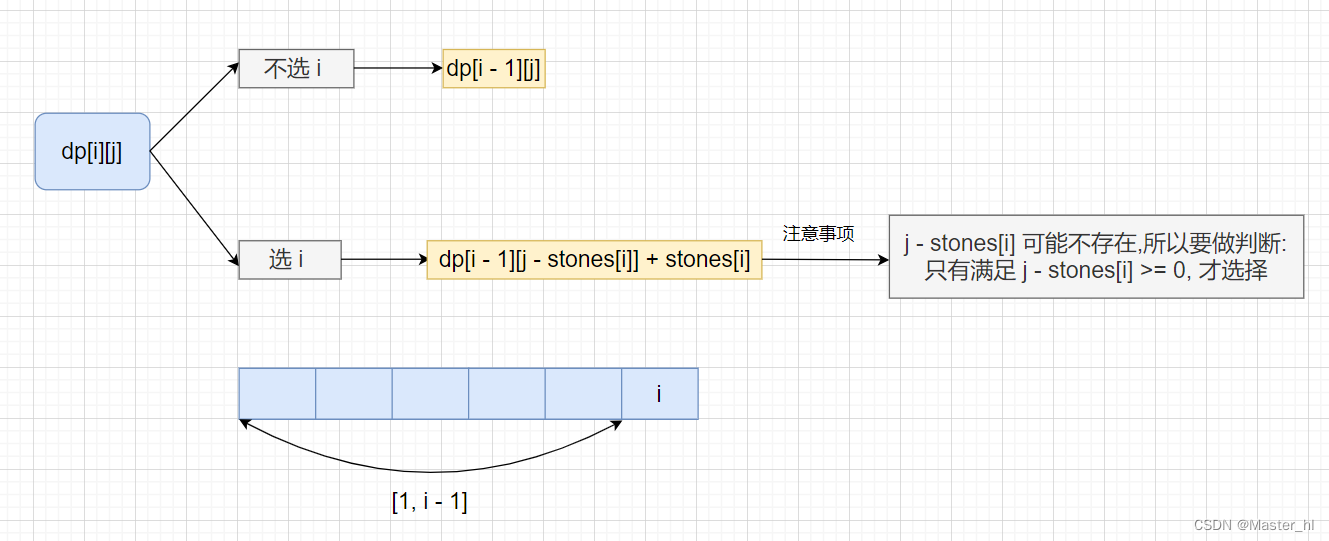
3. 编写代码

初始化过程模棱两可的时候务必要要画图去理解！

public int lastStoneWeightII(int[] stones) {
    int n = stones.length;
    int sum = 0;
    for(int i = 0; i < n; ++i) sum += stones[i];
    int aim = sum / 2;

    int[][] dp = new int[n + 1][aim + 1];
    // 状态定义：从前 i 个石头中挑选，重量之和不超过 j，此时重量的最大和
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j <= aim; ++j) {
            dp[i][j] = dp[i - 1][j]; // 不选 i
            if(j >= stones[i - 1]) {
                // 选 i
                dp[i][j] = Math.max(dp[i][j], 
                        dp[i - 1][j - stones[i - 1]] + stones[i - 1]);
            }
        }
    }
    // 求出 a 的值后, b 就等于 sum - a, 那么最后的重量就是 sum - 2 * dp[n][aim]
    return (int)Math.abs(sum - 2 * dp[n][aim]);
}

4. 空间优化

public int lastStoneWeightII(int[] stones) {
    int n = stones.length;
    int sum = 0;
    for(int i = 0; i < n; ++i) sum += stones[i];
    int aim = sum / 2;

    int[] dp = new int[aim + 1];
    // 状态定义：从前 i 个石头中挑选，重量之和不超过 j，此时重量的最大和
    for(int i = 1; i <= n; i++) {
        for(int j = aim; j >= stones[i - 1]; --j) {
            dp[j] = Math.max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);
        }
    }
    // 求出 a 的值后, b 就等于 sum - a, 那么最后的重量就是 sum - 2 * dp[aim]
    return (int)Math.abs(sum - 2 * dp[aim]);
}

对于本科生，01 背包类型彻底理解这几道，基本上能解决面试中大部分问题了，虽然感觉上，中大公司今年的趋势是面项目和手撕算法比较多，但是金九银十已经过去一个月了，算法也不是一朝一夕就能提升来的，所以重心还是在八股和项目，最后祝大家都能在秋招拿到自己满意的 offer~