问题描述:

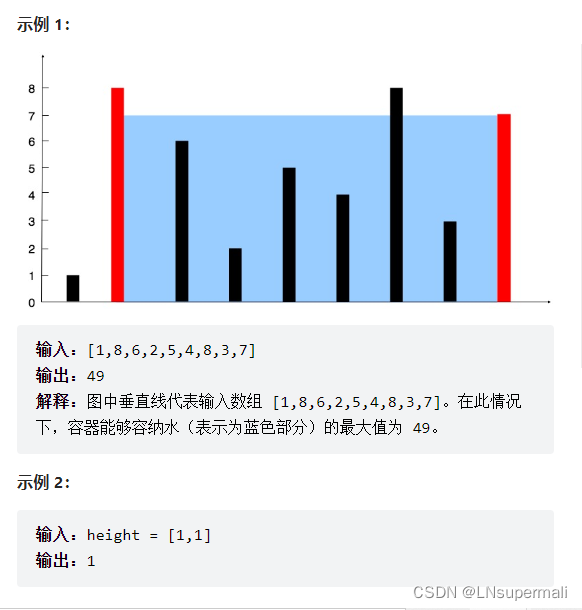
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

解题思路：

本题目被力扣归纳到双指针类题型中！所以在官方的提示下我们该就如何运用双指针算法进行思考。
我们首先看示例1的图像，我们可以较容易地将所求问题抽象为求由水柱长度构成地矩形面积地最大值，同时要保证以较短地水柱构成边，而这个矩形地面积可看成由两边向内变动，所以我们可以进一步想到使用对撞双指针来解决问题。具体操作如下：

1.定义左右指针分别指向数组的开头与结尾，以左右指针中指向值的较小值作为“矩形的宽”乘以此时左右指针的距离(即此时“矩形的长”)作为此时的面积
2.若左指针指向的值小于等于此时右指针指向的值，则将左指针向右边移动一位，否则右指针向左移动一位，同时更新取出此时最大的“矩形面积”

代码：

class Solution {
	//Two Pointer
	//Time Complexity: O(N)
	//Space Complexity: O(1)
	public int maxArea(int[] height) {
		int left = 0;
		int right = height.length - 1;
		//定义结果变量用于记录当前最大的面积
		int res = 0;
		//循环条件
		//左指针小于右指针
		while (left < right) {
			//计算当前的面积
			//以较小边为“矩形”的宽
			int area = Math.min(height[left],height[right]) * (right - left);
			//更新并取出当前的最大面积
			res = Math.max(area,res);
			if (height[left] <= height[right]) {
				left++;
			} else {
				right--;
			}
		}
		return res;
	}
}