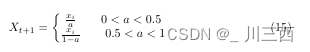一、题目描述与要求

按之字形顺序打印二叉树_牛客题霸_牛客网 (nowcoder.com)

题目描述

给定一个二叉树，返回该二叉树的之字形层序遍历，（第一层从左向右，下一层从右向左，一直这样交替）

数据范围：0≤n≤1500,树上每个节点的val满足 ∣val∣<=1500
要求：空间复杂度：O(n)，时间复杂度：O(n)

例如：
给定的二叉树是{1,2,3,#,#,4,5}

该二叉树之字形层序遍历的结果是

[

[1],

[3,2],

[4,5]

]

示例

示例1：

输入：{1,2,3,#,#,4,5}

返回值：[[1],[3,2],[4,5]]

说明：如题面解释，第一层是根节点，从左到右打印结果，第二层从右到左，第三层从左到右。

示例2：

输入：{8,6,10,5,7,9,11}

返回值：[[8],[10,6],[5,7,9,11]]

示例3：

输入：{1,2,3,4,5}

返回值：[[1],[3,2],[4,5]]

---

二、解题思路

根据题目描述可以知道，我们需要对所给的二叉树进行层次遍历，这就需要用到队列，我们依次讲每层的结点存入队列，然后再将每一层的结点的值存到vector中，每一层一个vector。

此时我们需要解决怎么去实现“之字形”，也就是根结点按照从左到右输出，下面开始第一行按照从右到左，第二行按照从左到右...，由此可以看出，奇数行的需要进行翻转，而偶数行的不需要翻转（根结点为第0层）。所以我们设置一个标志flag，初始为true，然后每次进入while循环时进行改变，第一次是根结点，也就是第0行，标志置为false，不需要进行反转。

首先我们判断二叉树是否为空，为空的话直接返回空vector；

然后定义队列，用来对二叉树进行层次遍历，将根结点先压入，然后当队列不为空的时候进入while循环，然后就定义用来存储每一行结点的值的vector。队列大小根据每一层结点的数量进行变化。

然后就是将队列中存储的结点依次弹出，并将对应的值存入vector中，然后再将下一层的结点存入队列中。然后判断当前层次是否需要反转，需要的话调用reverse将vector进行反转，然后将vector存入v中。

最后返回v即可。

---

三、具体代码

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pRoot TreeNode类 
     * @return int整型vector<vector<>>
     */
    vector<vector<int> > Print(TreeNode* pRoot) {
        // write code here
        TreeNode* head=pRoot;
        vector<vector<int>> v;
        if(head==nullptr) return v;//如果为空树则直接返回空vector
        //利用队列进行层次遍历
        queue<TreeNode*> q;
        q.push(head);//将根结点压入队列
        TreeNode *p;
        bool flag=true;
        while(!q.empty()){ //当队列不为空时
            //记录二叉树的某一行
            vector<int> row;
            int n=q.size();
            //奇数行反转，偶数行不反转
            flag=!flag;
            //每层有几个结点，队列大小就是多少
            for(int i=0;i<n;i++){
                p=q.front();
                q.pop();
                row.push_back(p->val);
                //左右子树不为空，存入左右子树为下一个层次
                if(p->left) q.push(p->left);
                if(p->right) q.push(p->right);
            }
            if(flag) reverse(row.begin(),row.end());
            v.push_back(row);
        }
        return v;
    }
};