【面试HOT100】哈希双指针滑动窗口

系列综述：
💞目的：本系列是个人整理为了秋招面试的，整理期间苛求每个知识点，平衡理解简易度与深入程度。
🥰来源：材料主要源于LeetCodeHot100进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也可能含有少量的个人实验自证。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈【C++】秋招&实习面经汇总篇

文章目录

- - 基本算法
  - 哈希篇
  - - 1. 两数之和
    - 49. 字母异位词分组
    - 128. 最长连续序列
  - 双指针篇
  - - 283. 移动零
    - 11. 盛最多水的容器
    - 15. 三数之和
    - 42. 接雨水
  - 滑动窗口篇
  - - 3. 无重复字符的最长子串
    - 438. 找到字符串中所有字母异位词

😊点此到文末惊喜↩︎

基本算法

排序
set去重
哈希：数组全部扔入unordered_map可通过O(1)时间进行查找

哈希篇

1. 两数之和

问题
- 给定一个整数数组 nums 和一个整数目标值 target
- 在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。
思路
- 暴力方法
- 两次遍历
  - 第一次利用数组初始化哈希表
  - 第二次寻找非自身节点的目标结点
- 单次遍历
  - 拿起一个看看和口袋中是否有一样的，没有则放入口袋

vector<int> twoSum(vector<int>& nums, int target) {
    unordered_map<int, int> umap;	// 哈希表：存放数组中元素的位置和下标
    vector<int> res(2,-1);	
    for (int i = 0; i < nums.size(); i++) {
    	// 若含有目标元素，则赋值并结束循环
        if (umap.count(target-nums[i]) > 0) { // *判断是否含有元素
            res[0]=a[target-nums[i]];
            res[1]=i;
            break;
        }
        // 没有则记录
        umap[nums[i]]=i;	// *map的插入：key为数组元素，value为数组下标
    }
    return res;
};

总结
- unordered_map比map更加节省空间
- 使用if (umap.count(target_key) > 0)，判断目标元素是否存在

49. 字母异位词分组

问题
- 字母异位词是由重新排列源单词的所有字母得到的一个新单词。
- 给你一个字符串数组，请你将字母异位词组合在一起
思路
- 简化：key是唯一性标识，value是任意类型的目标

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        unordered_map <string,vector<string> > m;
        for(const string& s : strs) {
            string t = s;	// 利用字符串进行比较
            sort(t.begin(),t.end());
            m[t].push_back(s);  
        }
        for(auto& n : m) 
            res.push_back(n.second);
        return res;
    }
};

128. 最长连续序列

问题
- 给定一个未排序的整数数组 nums
- 找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。
- 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
思路
- 通过数组初始化unordered_set，方便O(1)时间的查找
- 去重优化：最长子序列一定是从最小的开始的，所有若n-1存在则直接跳过

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int res = 0;
        unordered_set<int> s(nums.begin(), nums.end());
        for(auto &n : s) {
        	// 健壮性检查：去重
            if(s.count(n-1)) continue; 
            // 初始化、算法、收尾
            int cnt = 0;
            while(s.count(n++)) ++cnt;
            res = max(res, cnt);
        }
        return res;
    }
};

双指针篇

283. 移动零

问题
- 给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾
- 同时保持非零元素的相对顺序。
思路
- 快慢指针 + 交换

void moveZeroes(vector<int>& nums) {
   int slow = 0, fast = 0;
    while (fast < nums.size()) {
        if (nums[fast] != 0) {
            swap(nums[slow], nums[fast]);
            slow++;
        }
        ++fast;
    }
}

11. 盛最多水的容器

问题
- 给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i])
- 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水，返回容器可以储存的最大水量。
思路
- 边界双指针：左右边界向中间慢慢收缩

int maxArea(vector<int>& height) {
     int left = 0, right = height.size() - 1
     int res = 0;
     while(left < right) {
         res = height[left] < height[right] ? 
             max(res, (right - left) * height[right++]): 
             max(res, (right  - left) * height[right--]); 
     }
     return res;
 }

待定思路
- 左边向中间找更高，记录最值，右边向中间找更高，记录最值。

15. 三数之和

问题
- 给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。
- 返回所有和为 0 且不重复的三元组。
- 答案中不可以包含重复的三元组。
思路
- 排序 + 分类讨论 + 去重

vector<vector<int>> threeSum(vector<int>& nums) {
    vector<vector<int>> result;
    sort(nums.begin(), nums.end()); // 排序：从小到大
    // 找出a + b + c = 0
    // a = nums[i], b = nums[left], c = nums[right]
    for (int i = 0; i < nums.size(); i++) {
        // 健壮性检查
        if (nums[i] > 0) return result;	// 排序若首元素已大于零，则不可能凑出结果
        if (i > 0 && nums[i] == nums[i - 1])// i的去重：i和已使用过的i-1比较，才是三元组间的去重
        	continue;
        // 初始化
        int left = i + 1;
        int right = nums.size() - 1;
        // 算法部分
        while (left < right) {
        	// 情况分类讨论
            if (nums[i] + nums[left] + nums[right] > 0) right--;
            else if (nums[i] + nums[left] + nums[right] < 0) left++;
            else {
                // key：注意如何进行vector的直接构造压入
                result.push_back(vector<int>{nums[i], nums[left], nums[right]});
                // 对left和right的去重
                while (left < right && nums[right] == nums[right - 1]) right--;
                while (left < right && nums[left] == nums[left + 1]) left++;
                // 找到答案时，双指针同时收缩
                right--;
                left++;   
            }
        }
    }
    return result;
}

42. 接雨水

问题
- 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图
- 计算按此排列的柱子，下雨之后能接多少雨水。
思路
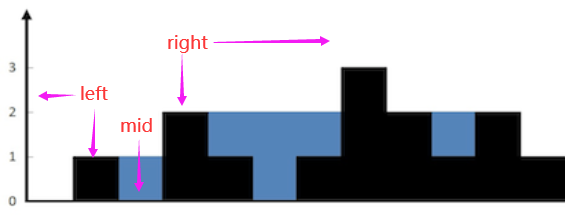
- 分类讨论：更大、更小、相等

// 接雨水
int trap(vector<int>& height) {
    if (height.size() <= 2) return 0; // 可以不加
    stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度
    st.push(0);
    int sum = 0;
    for (int i = 1; i < height.size(); i++) {
        if (height[i] < height[st.top()]) {     // 情况一
            st.push(i);
        } if (height[i] == height[st.top()]) {  // 情况二
            st.pop(); // 其实这一句可以不加，效果是一样的，但处理相同的情况的思路却变了。
            st.push(i);
        } else {      
            // 将i之前的比i小的全部凹槽计算水量
            while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
                int mid = st.top();
                st.pop();
                if (!st.empty()) {  
                    int h = min(height[st.top()], height[i]) - height[mid];
                    int width = i - st.top() - 1; 
                    sum += h * w;
                }
            }
            st.push(i);
        }
    }
    return sum;
}
// 优化
// 接雨水
int trap(vector<int>& height) {
    if (height.size() <= 2) return 0; // 可以不加
    stack<int> st; // 存着下标，计算的时候用下标对应的柱子高度
    st.push(0);
    int sum = 0;
    for (int right = 1; right < height.size(); right++) {
        // 将前面小的全部出栈：计算right前的比height[right]的全部凹槽计算水量
        while (!st.empty() && height[right] > height[st.top()]) { 
            int mid = st.top();
            st.pop();
            if (!st.empty()) {  
                // st.top()为left的下标，即左右两柱-底部高度为水槽高度
                int left = st.top();
                int depth = min(height[left], height[right]) - height[mid];
                int width = right - left - 1; 
                sum += depth * width;
            }
        }
        st.push(right);
    }
    return sum;
}

滑动窗口篇

解决的问题：
给定一个线性表（字符串、数组等），一次遍历求满足指定条件的连续子部分

3. 无重复字符的最长子串

问题
- 给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。
思路
- 滑动窗口

int lengthOfLongestSubstring(string s) {
    const int N = s.size();
    if (N < 2) return N;

    int res = 0;
    unordered_map<char, int> umap;
    umap[s[0]] = 0;
    int slow = 0, fast = 1;
    while (fast < N) {
        // 缩小窗口：必须保证重复字符在滑动窗口内，因为过去的字符仍然在窗口内
        if (umap.count(s[fast]) > 0 && slow <= umap[s[fast]]) // 后半段判断的含义？
            slow = umap[s[fast]] + 1;
        // 扩大窗口
        umap[s[fast]] = fast;
        ++fast;
        res = max(fast-slow, res);
    }
    return res;

}

438. 找到字符串中所有字母异位词

问题
- 给定两个字符串 s 和 p，找到 s 中所有 p 的异位词的子串，返回这些子串的起始索引。
- 异位词指由相同字母重排列形成的字符串（包括相同的字符串）。
思路
- 快慢指针 + 交换

// 返回字符串 s 中包含字符串 t 的全部字符的最小窗口
string SlideWindow(string s, string t) {
	// need记录子串情况，window记录合适窗口
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
	
    int left = 0, right = 0;
    // 记录最小覆盖子串的起始索引及长度
    int start = 0, len = INT_MAX;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];	// c 是将移入窗口的字符
        right++;			// 右移窗口
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }
        while (valid == need.size()) {	// TODO：收缩条件
	        // TODO：更新结果记录
            if (right - left < len) {	
                start = left;// 更新起始值
                len = right - left;// 最小长度
            }
            // 收缩窗口
            char d = s[left];
            left++;
 			// TODO：收缩处理
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }                    
        }
    }
    // 返回最小覆盖子串
    return len == INT_MAX ?
        "" : s.substr(start, len);
}