绪论

数值分析概念

用计算机求解数学问题的数值方法和理论

三大科学研究方法

• 实验
• 理论分析
• 科学计算（用计算机去辅助研究）：数值方法+计算机

解析解和近似解

• 解析解：使用数学方法求出或推导出的结果，往往可以求解出原问题的精确解，但是所列出的方程也不一定完全匹配现实问题，这时候所得到的解析解和现实也是有误差的

• 近似数值解：解析表达式难以给出，通过采用数学理论与计算机结合，并使用合适的算法所得到的问题的近似解，只要解的误差在可接受范围之内即可

数值分析的关键工作

• 寻找能找到问题近似解的方法
• 分析该方法的可靠性（如误差、稳定性、收敛性）

事实上，电子计算机实质上只会做有限次的加、减、乘、除等基本运算，研究怎样通过计算机所能执行的基本运算，求得各类数学问题的数值解或近似解就是数值计算(科学计算)的根本课题。由基本运算及运算顺序的规定所构成的完整的解题步骤，称为算法。数值计算的根本任务就是研究算法。

案例

sinx求解

使用理论方法：泰勒公式，将复杂的问题 转化为 简单问题的重复循环，这样计算机就可以求解了

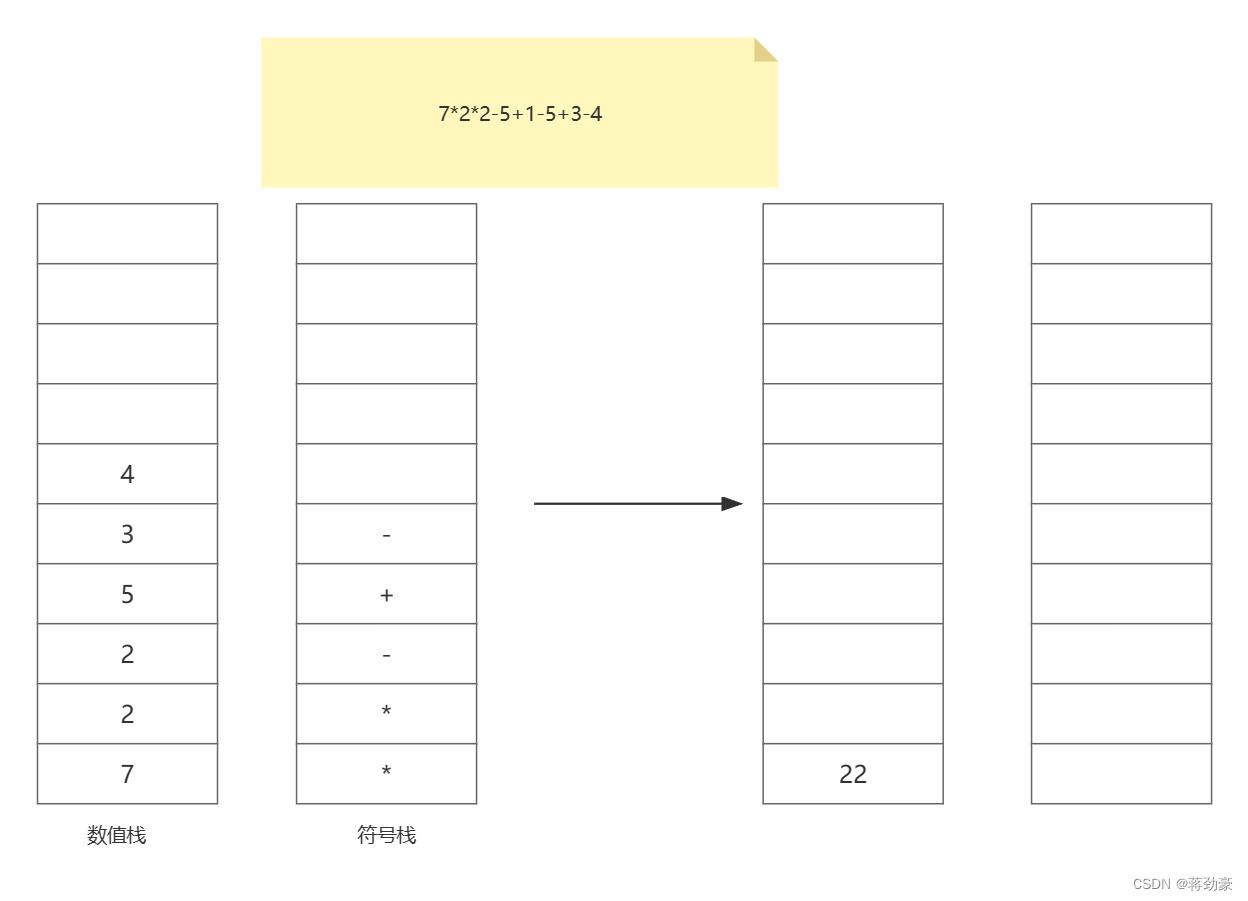
计算多项式

上面的方法是秦九韶算法（1247提出），也是后面提出的Horner算法（1819）

【总结】

一个问题可以有多种计算方法，不同的计算方法的效率可能不同

线性方程组

Cramer法则是可以求解任何的线性方程组的，但是求解时间太长，因此需要换一种方法来计算，如高斯消元法

其他问题

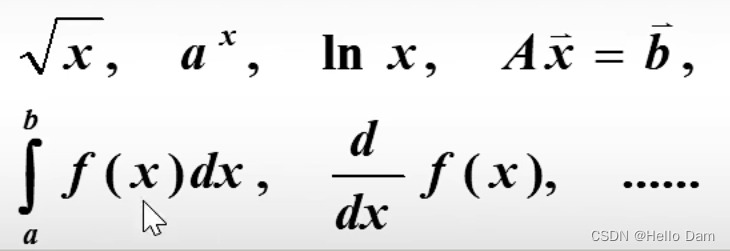
说明

文章为本人学习网上课程的学习笔记，课程的链接为 《数值分析》2020年春季华中科技大学研究生课程 46讲合辑，文章中大部分图片来源于课程截图，部分图片中加上了本人的理解标注，如有侵权，麻烦联系删除，最后对老师的课程表示衷心的感谢。