多标签学习这个方向问题比较多,可以参考多标签学习的新趋势(2021 Survey TPAMI) 和 部分标签学习和缺失标签学习到底什么异同? 这两篇偏综述性质的解释。本文重点解释下面几个重点问题:
Multi Label Classification with Missing Labels(MLML)和Partial Multi-Label Learning(PML)的区别
- MLML重点在Missing Labels,一张图标注员一般只打标少量实体,大量的实体miss掉了,产生了大量的False Negative cases。
- PML重点在很多信息不明确,很难标。例如下面图,诸如Tree、Lavender这些标签相对是比较简单的。但是有些标签到底有没有,是比较难以确定的,对于某些标注者,可能出现:“这张图片看起来是在法国拍的,好像也可能是意大利?”,这种情况称之为Ambiguous。PML希望把所有的ambiguous都标出来,所以PML选择的是让标注者提供所有可能的标签,当然加了一个较强的假设:所有的标签都应该被包含在候选标签集中。

MLML的loss设计
刚提到MLML的问题在于大量正例标签miss掉了,有不少False Positive,从loss推导角度来分析下这个问题
Preliminary
MLML问题一般理解为针对每一个label进行one-vs.-rest的二分类:
-
对于多分类,假设存在n类,那么对于每个样本经过神经网络会出n个logits,这n个logits过softmax得到和为1的值再过NLL的loss,就是CrossEntropy,详细可以参考信息熵 条件熵 交叉熵 联合熵 相对熵 KL散度 SCE MAE 互信息(信息增益)里的推导,所以 C E ( P , Q ) = − ∑ i ∈ [ 0 , n − 1 ] p i l o g q i CE(P,Q)=-\sum_{i \in [0,n-1]}p_ilogq_i CE(P,Q)=−∑i∈[0,n−1]pilogqi,一般 p i p_i pi是label, q i q_i qi是经过softmax后的结果。
-
对于二分类,对于每个样本经过神经网络可以只出一个logit,那么这个logit只过sigmoid得到p就可以了,都没softmax啥事。但算CE loss需要另外一个logit归一化的结果,也就是1-p,也需要另外一个label就是1-y。所以到二分类里 C E ( P , Q ) = − ∑ i ∈ [ 0 , 1 ] p i l o g q i = − y l o g p − ( 1 − y ) l o g ( 1 − p ) CE(P,Q)=-\sum_{i \in [0,1]}p_ilogq_i=-ylogp-(1-y)log(1-p) CE(P,Q)=−∑i∈[0,1]pilogqi=−ylogp−(1−y)log(1−p),y是label,p是经过sigmoid后的结果。
在Simple and Robust Loss Design for Multi-Label Learning with Missing Labels一文中,Loss被一般化地定义为下面表达式,值得注意的是K是表示有K个二分类,而不是K=2,
y
i
y_i
yi的取值是0或者1
L
=
−
∑
i
=
1
K
(
y
i
L
i
+
+
(
1
−
y
i
)
L
i
−
)
L= -\sum_{i=1}^K(y_iL_i^++(1-y_i)L_i^-)
L=−i=1∑K(yiLi++(1−yi)Li−)
如果是BCE就是下面表达式,
p
i
p_i
pi表示的是第i个二分类经过sigmoid后只出了一个值
p
i
=
σ
(
x
i
)
=
1
1
+
e
−
x
i
p_i=\sigma(x_i)=\frac{1}{1+e^{-x_i}}
pi=σ(xi)=1+e−xi1,其中
x
i
x_i
xi就是经过神经网络后第i个二分类只出了一个值
L
=
−
∑
i
=
1
K
(
y
i
L
i
+
+
(
1
−
y
i
)
L
i
−
)
L
i
+
=
l
o
g
p
i
L
i
−
=
l
o
g
(
1
−
p
i
)
L= -\sum_{i=1}^K(y_iL_i^++(1-y_i)L_i^-) \\ L_i^+=logp_i \\ L_i^-=log(1-p_i)
L=−i=1∑K(yiLi++(1−yi)Li−)Li+=logpiLi−=log(1−pi)
有了这个表达式可以推导一下导数结果,因为
σ
′
(
x
i
)
=
σ
(
x
i
)
(
1
−
σ
(
x
i
)
)
=
p
i
∗
(
1
−
p
i
)
\sigma^{'}(x_i)=\sigma(x_i)(1-\sigma(x_i))=p_i*(1-p_i)
σ′(xi)=σ(xi)(1−σ(xi))=pi∗(1−pi):
∂
L
i
−
∂
x
i
=
1
p
i
−
1
∗
p
i
∗
(
1
−
p
i
)
=
−
p
i
\frac{\partial L_i^-}{\partial x_i} = \frac{1}{p_i-1}*p_i*(1-p_i)=-p_i
∂xi∂Li−=pi−11∗pi∗(1−pi)=−pi
所以Simple and Robust Loss Design for Multi-Label Learning with Missing Labels一文中Fig 3对应的BCE是一条直线,注意横轴是p,纵轴是
−
∂
L
i
−
∂
x
i
-\frac{\partial L_i^-}{\partial x_i}
−∂xi∂Li−
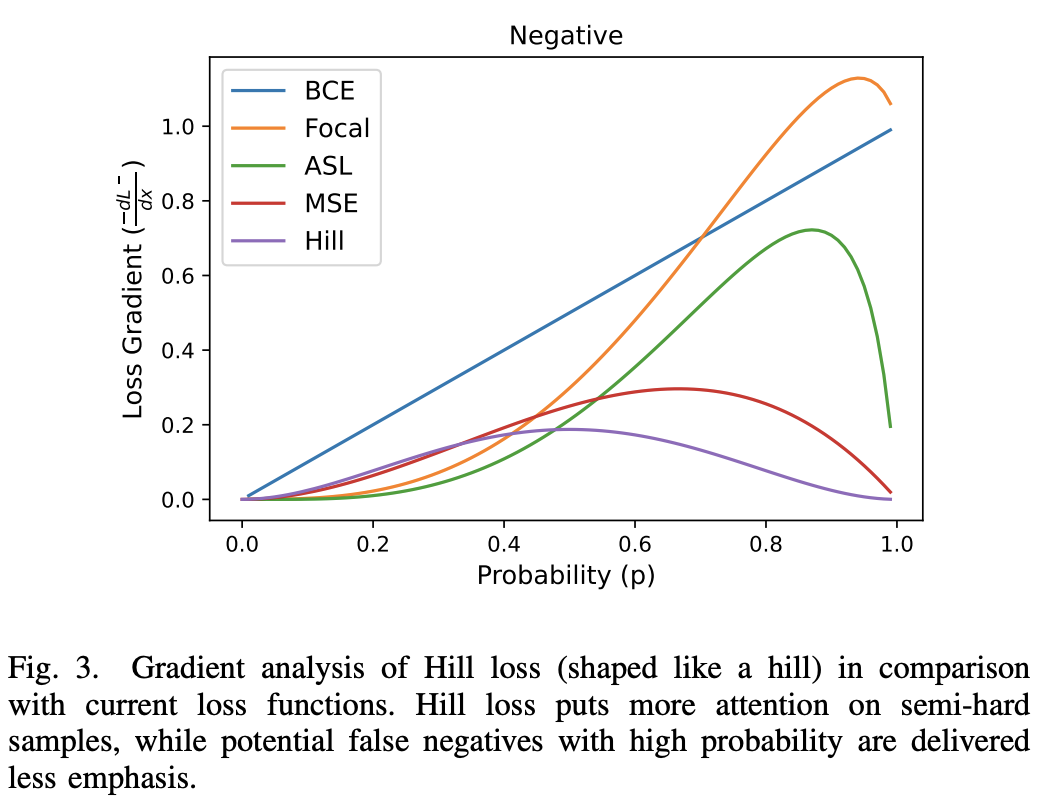
如果是Focal Loss就是下面表达式,
γ
\gamma
γ is a focus parameter, and
α
+
\alpha_+
α+ and
α
−
\alpha_-
α− are utilized to balance positives and negative
L
=
−
∑
i
=
1
K
(
y
i
L
i
+
+
(
1
−
y
i
)
L
i
−
)
L
i
+
=
α
+
(
1
−
p
i
)
γ
l
o
g
p
i
L
i
−
=
α
−
p
i
γ
l
o
g
(
1
−
p
i
)
L= -\sum_{i=1}^K(y_iL_i^++(1-y_i)L_i^-) \\ L_i^+=\alpha_+(1-p_i)^\gamma logp_i \\ L_i^-=\alpha_-p_i^\gamma log(1-p_i)
L=−i=1∑K(yiLi++(1−yi)Li−)Li+=α+(1−pi)γlogpiLi−=α−piγlog(1−pi)
ASL(Asymmetric Loss For Multi-Label Classification)
ASL Loss是一种对Focal Loss的修正,其中
p
m
=
m
a
x
(
p
−
m
,
0
)
p_m=max(p-m,0)
pm=max(p−m,0), The
probability margin m ≥ 0 is a tunable hyper-parameter。 The ASL loss reduces the weight of easy negatives via using
γ
+
<
γ
−
\gamma+<\gamma-
γ+<γ−, and discards negatives with low predicted probability via
the m shifted probability
L
=
−
∑
i
=
1
K
(
y
i
L
i
+
+
(
1
−
y
i
)
L
i
−
)
L
i
+
=
(
1
−
p
m
)
γ
+
l
o
g
p
m
L
i
−
=
p
m
γ
−
l
o
g
(
1
−
p
m
)
L= -\sum_{i=1}^K(y_iL_i^++(1-y_i)L_i^-) \\ L_i^+=(1-p_m)^{\gamma+} logp_m \\ L_i^-=p_m^{\gamma-} log(1-p_m)
L=−i=1∑K(yiLi++(1−yi)Li−)Li+=(1−pm)γ+logpmLi−=pmγ−log(1−pm)
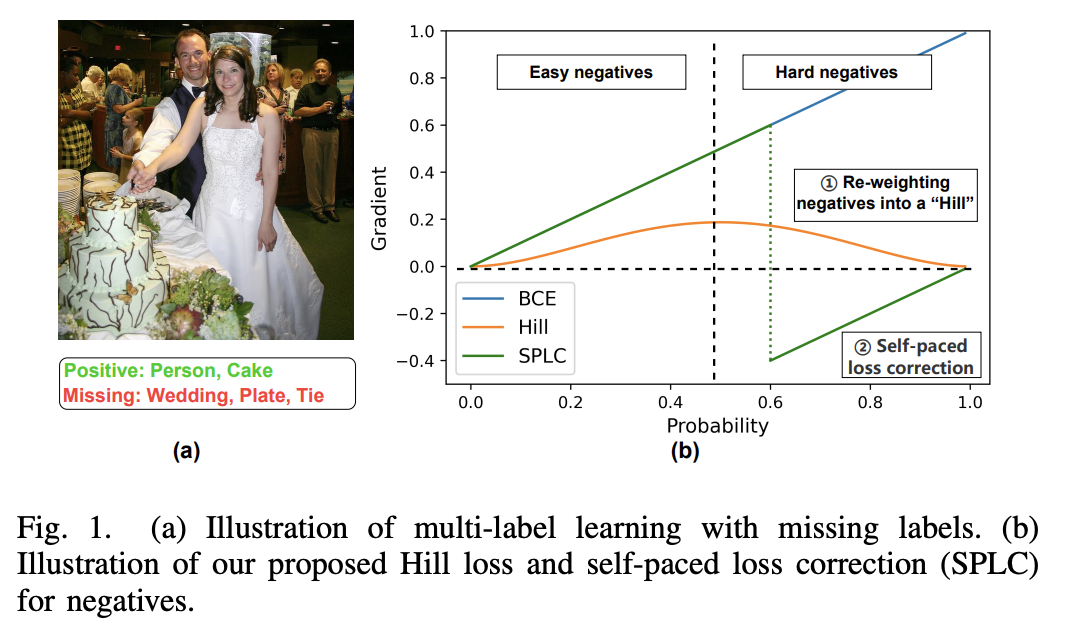
Hill Loss和SPLC Loss
来自Simple and Robust Loss Design for Multi-Label Learning with Missing Labels,简单来说就是把上述BCE收到missing labels影响做了一些修正,详细看原文较好
部分摘录自:
- https://www.zhihu.com/question/418818026/answer/1454922545
- https://zhuanlan.zhihu.com/p/266749365
- Asymmetric Loss For Multi-Label Classification
- Simple and Robust Loss Design for Multi-Label Learning with Missing Labels