文章目录
- 0 前言
- 1 课题说明
- 2 效果展示
- 3 具体实现
- 4 关键代码实现
- 5 算法综合效果
- 6 最后
0 前言
🔥 优质竞赛项目系列,今天要分享的是
🚩 基于深度学习的数学公式识别算法实现
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🥇学长这里给一个题目综合评分(每项满分5分)
- 难度系数:3分
- 工作量:4分
- 创新点:4分
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 课题说明
手写数学公式识别较传统OCR问题而言,是一个更复杂的二维手写识别问题,其内部复杂的二维空间结构使得其很难被解析,传统方法的识别效果不佳。随着深度学习在各领域的成功应用,基于深度学习的端到端离线数学公式算法,并在公开数据集上较传统方法获得了显著提升,开辟了全新的数学公式识别框架。然而在线手写数学公式识别框架还未被提出,论文TAP则是首个基于深度学习的端到端在线手写数学公式识别模型,且针对数学公式识别的任务特性提出了多种优化。
公式识别是OCR领域一个非常有挑战性的工作,工作的难点在于它是一个二维的数据,因此无法用传统的CRNN进行识别。
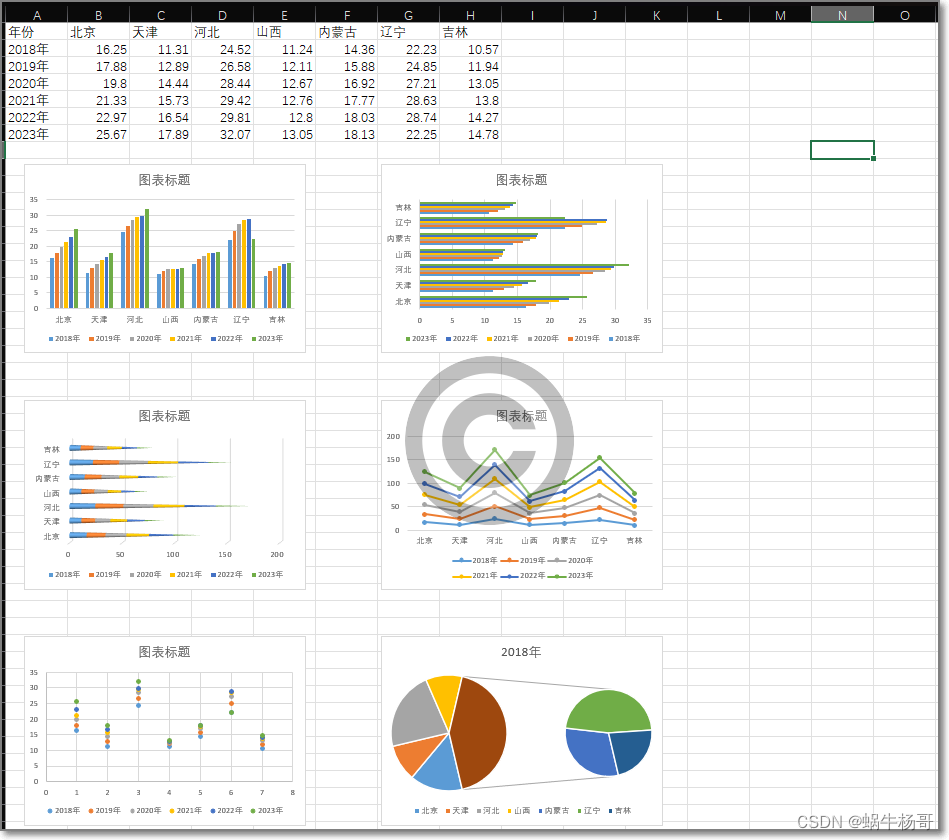
2 效果展示
这里简单的展示一下效果


3 具体实现
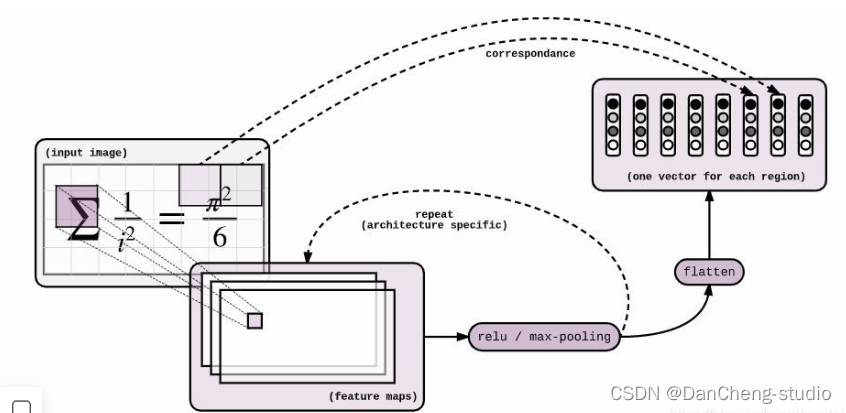
神经网络模型是 Seq2Seq + Attention + Beam
Search。Seq2Seq的Encoder是CNN,Decoder是LSTM。Encoder和Decoder之间插入Attention层,具体操作是这样:Encoder到Decoder有个扁平化的过程,Attention就是在这里插入的。具体模型的可视化结果如下
4 关键代码实现
class Encoder(object):
"""Class with a __call__ method that applies convolutions to an image"""
def __init__(self, config):
self._config = config
def __call__(self, img, dropout):
"""Applies convolutions to the image
Args:
img: batch of img, shape = (?, height, width, channels), of type tf.uint8
tf.uint8 因为 2^8 = 256,所以元素值区间 [0, 255],线性压缩到 [-1, 1] 上就是 img = (img - 128) / 128
Returns:
the encoded images, shape = (?, h', w', c')
"""
with tf.variable_scope("Encoder"):
img = tf.cast(img, tf.float32) - 128.
img = img / 128.
with tf.variable_scope("convolutional_encoder"):
# conv + max pool -> /2
# 64 个 3*3 filters, strike = (1, 1), output_img.shape = ceil(L/S) = ceil(input/strike) = (H, W)
out = tf.layers.conv2d(img, 64, 3, 1, "SAME", activation=tf.nn.relu)
image_summary("out_1_layer", out)
out = tf.layers.max_pooling2d(out, 2, 2, "SAME")
# conv + max pool -> /2
out = tf.layers.conv2d(out, 128, 3, 1, "SAME", activation=tf.nn.relu)
image_summary("out_2_layer", out)
out = tf.layers.max_pooling2d(out, 2, 2, "SAME")
# regular conv -> id
out = tf.layers.conv2d(out, 256, 3, 1, "SAME", activation=tf.nn.relu)
image_summary("out_3_layer", out)
out = tf.layers.conv2d(out, 256, 3, 1, "SAME", activation=tf.nn.relu)
image_summary("out_4_layer", out)
if self._config.encoder_cnn == "vanilla":
out = tf.layers.max_pooling2d(out, (2, 1), (2, 1), "SAME")
out = tf.layers.conv2d(out, 512, 3, 1, "SAME", activation=tf.nn.relu)
image_summary("out_5_layer", out)
if self._config.encoder_cnn == "vanilla":
out = tf.layers.max_pooling2d(out, (1, 2), (1, 2), "SAME")
if self._config.encoder_cnn == "cnn":
# conv with stride /2 (replaces the 2 max pool)
out = tf.layers.conv2d(out, 512, (2, 4), 2, "SAME")
# conv
out = tf.layers.conv2d(out, 512, 3, 1, "VALID", activation=tf.nn.relu)
image_summary("out_6_layer", out)
if self._config.positional_embeddings:
# from tensor2tensor lib - positional embeddings
# 嵌入位置信息(positional)
# 后面将会有一个 flatten 的过程,会丢失掉位置信息,所以现在必须把位置信息嵌入
# 嵌入的方法有很多,比如加,乘,缩放等等,这里用 tensor2tensor 的实现
out = add_timing_signal_nd(out)
image_summary("out_7_layer", out)
return out
学长编码的部分采用的是传统的卷积神经网络,该网络主要有6层组成,最终得到[N x H x W x C ]大小的特征。
其中:N表示数据的batch数;W、H表示输出的大小,这里W,H是不固定的,从数据集的输入来看我们的输入为固定的buckets,具体如何解决得到不同解码维度的问题稍后再讲;
C为输入的通道数,这里最后得到的通道数为512。
当我们得到特征图之后,我们需要进行reshape操作对特征图进行扁平化,代码具体操作如下:
N = tf.shape(img)[0]
H, W = tf.shape(img)[1], tf.shape(img)[2] # image
C = img.shape[3].value # channels
self._img = tf.reshape(img, shape=[N, H*W, C])
当我们在进行解码的时候,我们可以直接运用seq2seq来得到我们想要的结果,这个结果可能无法达到我们的预期。因为这个过程会相应的丢失一些位置信息。
位置信息嵌入(Positional Embeddings)
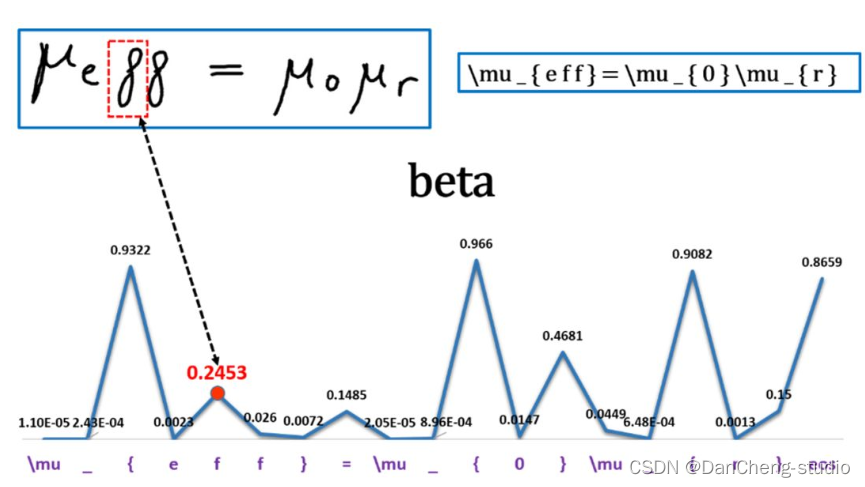
通过位置信息的嵌入,我不需要增加额外的参数的情况下,通过计算512维的向量来表示该图片的位置信息。具体计算公式如下:
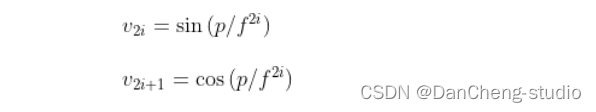
其中:p为位置信息;f为频率参数。从上式可得,图像中的像素的相对位置信息可由sin()或cos表示。
我们知道,sin(a+b)或cos(a+b)可由cos(a)、sin(a)、cos(b)以及sin(b)等表示。也就是说sin(a+b)或cos(a+b)与cos(a)、sin(a)、cos(b)以及sin(b)线性相关,这也可以看作用像素的相对位置正、余弦信息来等效计算相对位置的信息的嵌入。
这个计算过程在tensor2tensor库中已经实现,下面我们看看代码是怎么进行位置信息嵌入。代码实现位于:/model/components/positional.py。
def add_timing_signal_nd(x, min_timescale=1.0, max_timescale=1.0e4):
static_shape = x.get_shape().as_list() # [20, 14, 14, 512]
num_dims = len(static_shape) - 2 # 2
channels = tf.shape(x)[-1] # 512
num_timescales = channels // (num_dims * 2) # 512 // (2*2) = 128
log_timescale_increment = (
math.log(float(max_timescale) / float(min_timescale)) /
(tf.to_float(num_timescales) - 1)) # -0.1 / 127
inv_timescales = min_timescale * tf.exp(
tf.to_float(tf.range(num_timescales)) * -log_timescale_increment) # len == 128 计算128个维度方向的频率信息
for dim in range(num_dims): # dim == 0; 1
length = tf.shape(x)[dim + 1] # 14 获取特征图宽/高
position = tf.to_float(tf.range(length)) # len == 14 计算x或y方向的位置信息[0,1,2...,13]
scaled_time = tf.expand_dims(position, 1) * tf.expand_dims(
inv_timescales, 0) # pos = [14, 1], inv = [1, 128], scaled_time = [14, 128] 计算频率信息与位置信息的乘积
signal = tf.concat([tf.sin(scaled_time), tf.cos(scaled_time)], axis=1) # [14, 256] 合并两个方向的位置信息向量
prepad = dim * 2 * num_timescales # 0; 256
postpad = channels - (dim + 1) * 2 * num_timescales # 512-(1;2)*2*128 = 256; 0
signal = tf.pad(signal, [[0, 0], [prepad, postpad]]) # [14, 512] 分别在矩阵的上下左右填充0
for _ in range(1 + dim): # 1; 2
signal = tf.expand_dims(signal, 0)
for _ in range(num_dims - 1 - dim): # 1, 0
signal = tf.expand_dims(signal, -2)
x += signal # [1, 14, 1, 512]; [1, 1, 14, 512]
return x
得到公式图片x,y方向的位置信息后,只需要要将其添加到原始特征图像上即可。
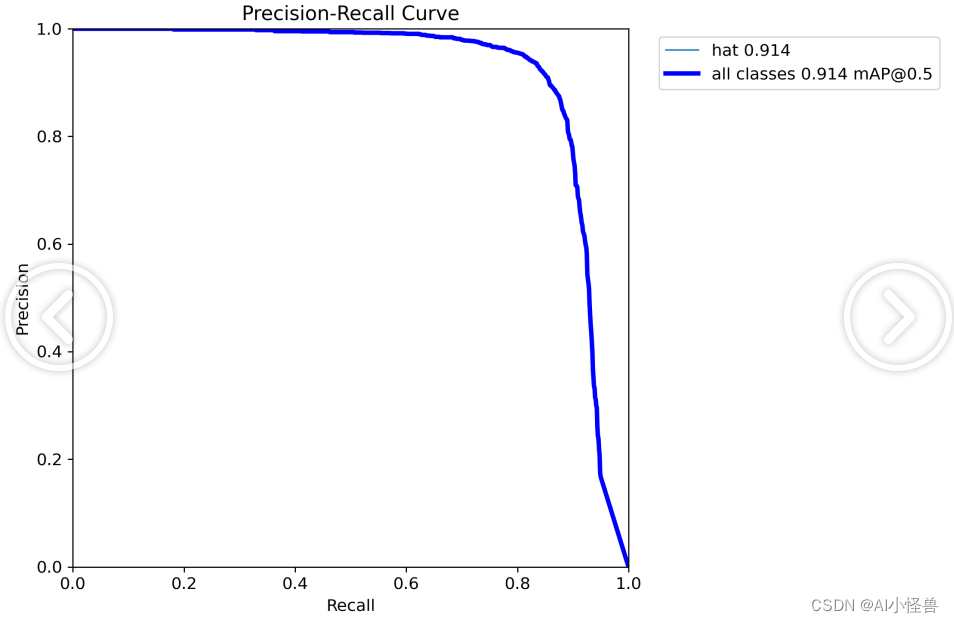
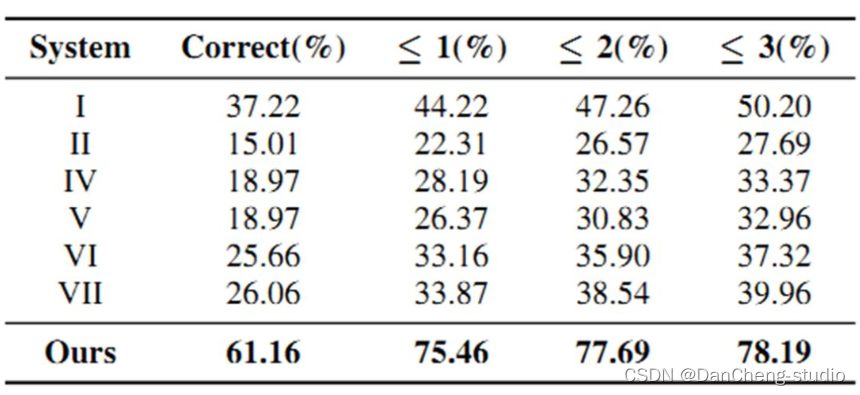
5 算法综合效果
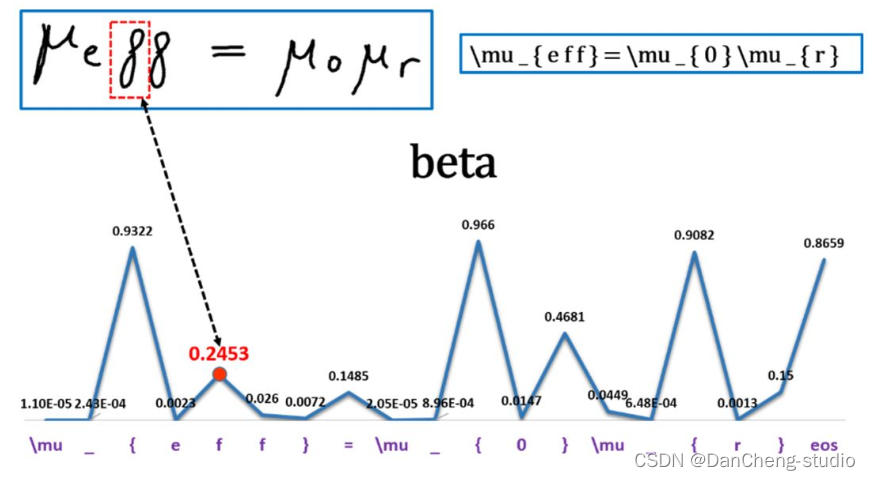
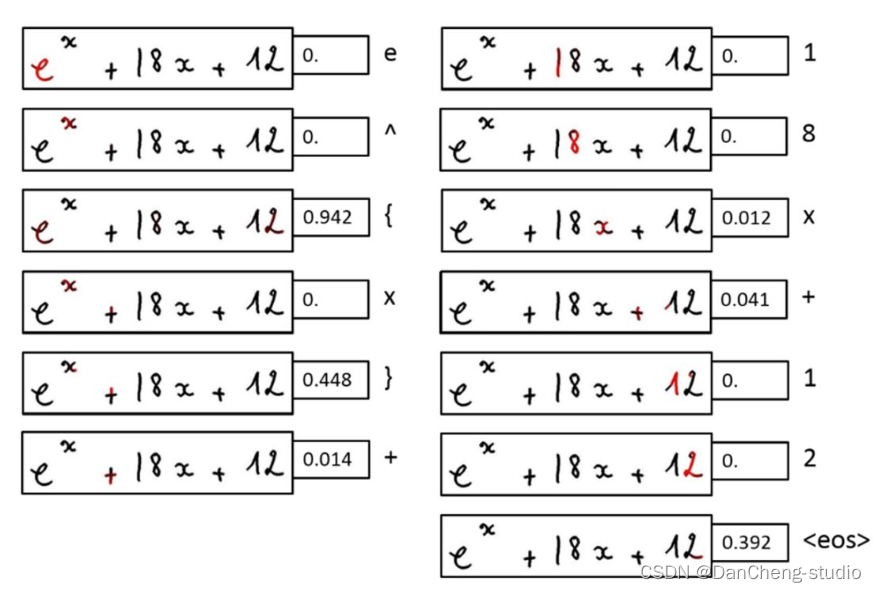
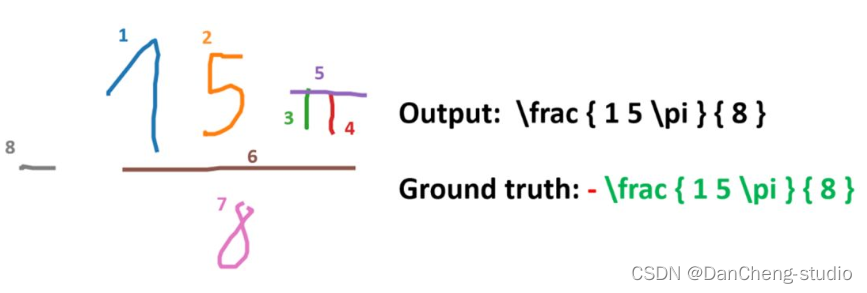
6 最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate