目录
第 11 例
第 12 例
第 13 例
第 14 例
第 15 例
第 16 例
第 17 例
第 18 例
第 19 例
第 20 例
第 11 例
程序源码:
/*
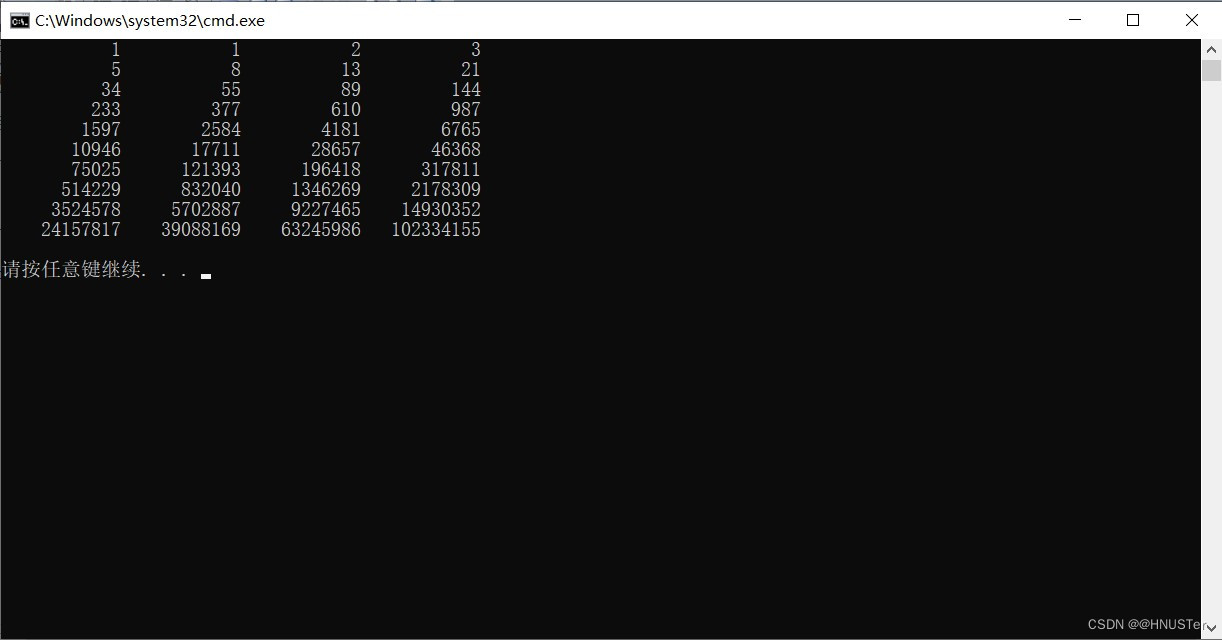
题目:古典问题(兔子生崽):有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不死,问每个月的兔子总数为多少?(输出前40个月即可)
程序分析:兔子的规律为数列1,1,2,3,5,8,13,21....,即下个月是上两个月之和(从第三个月开始)。
*/
#include<stdio.h>
int main()
{
int f1=1,f2=1,i;
for(i=1;i<=20;i++)
{
printf("%12d%12d",f1,f2);
if(i%2==0) printf("\n");
f1=f1+f2;
f2=f1+f2;
}
printf ("\n");
return 0;
}程序运行结果:
第 12 例
程序源码:
/*
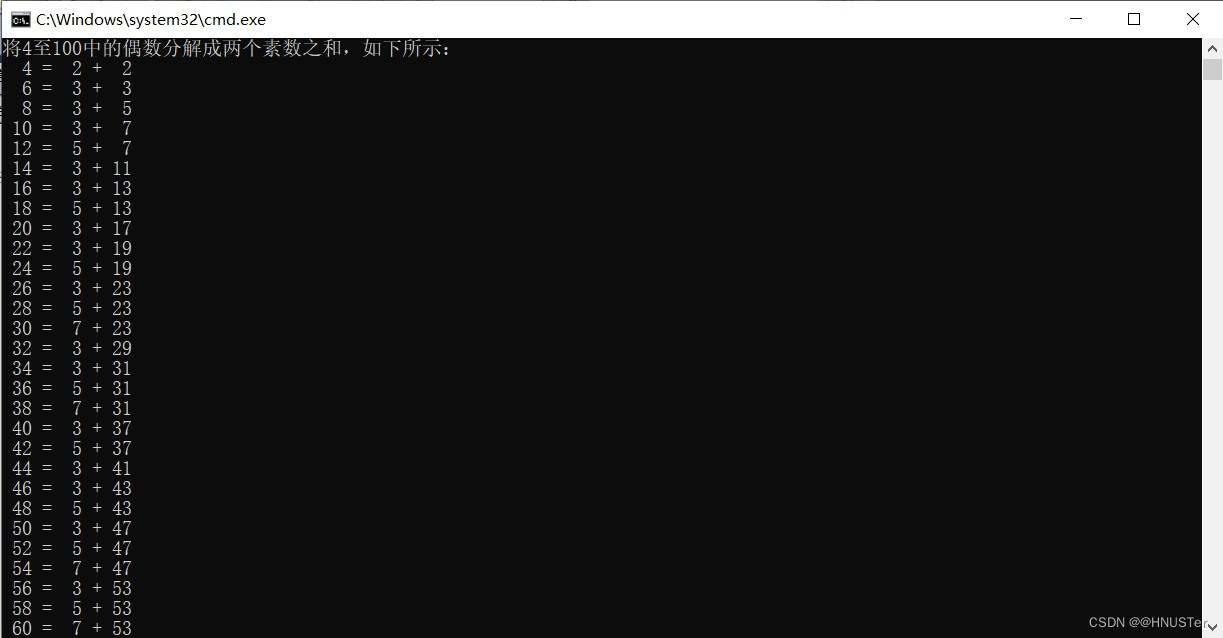
题目:将4至100中的偶数分解成两个素数之和。
程序分析:详见下面的代码。
*/
#include <stdio.h>
//自定义的函数。
int leap (int x)
{
int n,flag;
flag=1; //设flag的值为1,表示x是素数。
for (n=2;n<x;n++)
{
if (x%n==0)
{
flag=0;
break;
}
}
return flag;
}
//主函数。
int main ()
{
int x,a,b;
printf ("将4至100中的偶数分解成两个素数之和,如下所示:\n");
for (x=4;x<=100;x=x+2)
{
for (a=2;a<=x/2;a++)
{
if (leap(a)==1)
{
b=x-a;
if (leap(b)==1)
{
printf ("%3d = %2d + %2d\n",x,a,b);
break;
}
}
}
}
printf ("\n");
return 0;
}程序运行结果:
第 13 例
程序源码:
/*
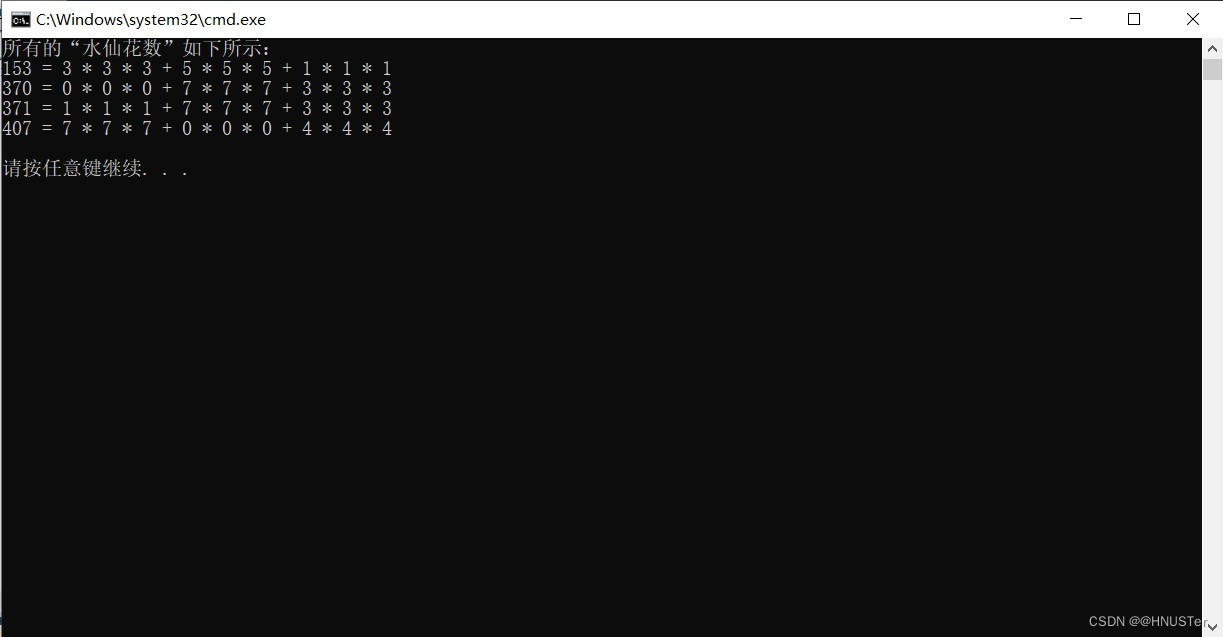
题目:打印出所有的"水仙花数",所谓"水仙花数"是指一个三位数,其各位数字立方和等于该数 本身。例如:153是一个"水仙花数",因为153=1的三次方+5的三次方+3的三次方。
程序分析:利用for循环控制100-999个数,每个数分解出个位,十位,百位。
*/
#include<stdio.h>
int main()
{
int i,x,y,z;
printf ("所有的“水仙花数”如下所示:\n");
for(i=100;i<1000;i++)
{
x=i%10;
y=i/10%10;
z=i/100%10;
if(i==(x*x*x+y*y*y+z*z*z))
printf("%d = %d * %d * %d + %d * %d * %d + %d * %d * %d\n",i,x,x,x,y,y,y,z,z,z);
}
printf ("\n");
return 0;
}程序运行结果:
第 14 例
程序源码:
/*
题目:将一个正整数分解质因数。例如:输入90,打印出90=2*3*3*5。
程序分析:对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于(小于的时候,继续执行循环)n,则说明分解质因数的过程已经结束,另外 打印出即可。
(2)但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数n.重复执行第二步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
*/
#include<stdio.h>
int main()
{
int n,i;
printf("请输入整数:");
scanf("%d",&n);
printf("%d = ",n);
for(i=2;i<=n;i++)
{
while(n%i==0)
{
printf("%d ",i);
n/=i;
if(n!=1) printf("* ");
}
}
printf("\n\n");
return 0;
}程序运行结果:

第 15 例
程序源码:
/*
题目:利用条件运算符的嵌套来完成此题:学习成绩>=90分的同学用A表示,60-89分之间的用B表示,60分以下的用C表示。
程序分析:(a>b)?a:b这是条件运算符的基本例子。
*/
#include<stdio.h>
int main()
{
float score;
char grade;
printf("请输入分数:");
scanf("%f",&score);
grade=(score>=90.0)?'A':((score>=60.0)?'B':'C');
printf("%c\n",grade);
printf ("\n");
return 0;
}程序运行结果:

第 16 例
程序源码:
/*
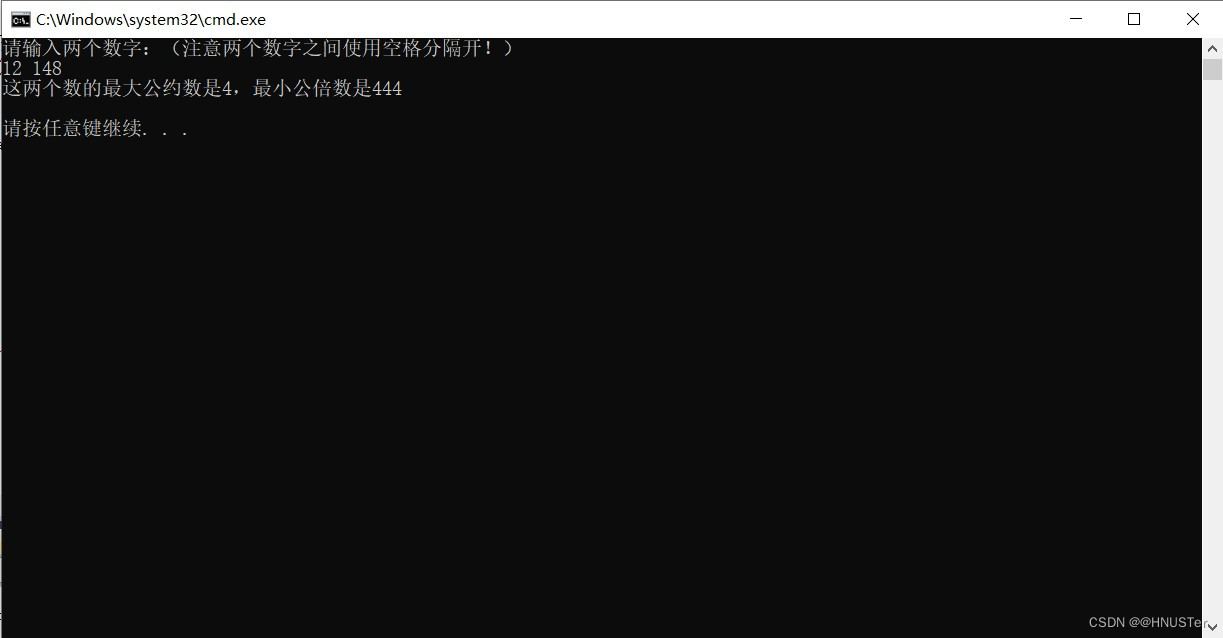
题目:输入两个正整数m和n,求其最大公约数和最小公倍数。
程序分析:
(1)最小公倍数=输入的两个数之积除于它们的最大公约数,关键是求出最大公约数。
(2)求最大公约数用辗转相除法(又名欧几里德算法)。
1)证明:
设c是a和b的最大公约数,记为c=gcd(a,b),a>=b,
令r=a mod b,
设a=kc,b=jc,则k,j互素,否则c不是最大公约数,
据上,r=a-mb=kc-mjc=(k-mj)c,
可知r也是c的倍数,且k-mj与j互素,否则与前述k,j互素矛盾,
由此可知,b与r的最大公约数也是c,即gcd(a,b)=gcd(b,a mod b),得证。
2)算法描述:
第一步:a ÷ b,令r为所得余数(r >= 0)。
第二步:互换:置 a←b,b←r,并返回第一步。
*/
#include<stdio.h>
int main()
{
int a,b,t,r,n;
printf("请输入两个数字:(注意两个数字之间使用空格分隔开!)\n");
scanf("%d %d",&a,&b);
if(a<b)
{
t=b;b=a;a=t;
}
r=a%b;
n=a*b;
while(r!=0)
{
a=b;
b=r;
r=a%b;
}
printf("这两个数的最大公约数是%d,最小公倍数是%d\n",b,n/b);
printf ("\n");
return 0;
}程序运行结果:
第 17 例
程序源码:
/*
题目:输入一行字符,分别统计出其中英文字母、空格、数字和其它字符的个数。
程序分析:利用while语句,条件为输入的字符不为'\n'。
*/
#include<stdio.h>
int main()
{
char c;
int letters=0,spaces=0,digits=0,others=0;
printf("请输入一行字符:\n");
while((c=getchar())!='\n')
{
if((c>='a'&&c<='z')||(c>='A'&&c<='Z'))
{
letters++;
}
else if(c>='0'&&c<='9')
{
digits++;
}
else if(c==' ')
{
spaces++;
}
else
{
others++;
}
}
printf("字母 %d 个\n数字 %d 个\n空格 %d 个\n其他 %d 个\n",letters,digits,spaces,others);
printf ("\n");
return 0;
}程序运行结果:

第 18 例
程序源码:
/*
题目:从键盘输入一个二维数组a,然后将二维数组a经过矩阵的转置得到二维数组b。
程序分析:详见下面的代码。
*/
#include <stdio.h>
#define N 2
#define M 3
int main ()
{
//定义二维整型数组a和b。
int a[N][M];
int i,j,b[M][N];
printf ("请输入二维整型数组a的6个元素:\n");
//利用双重循环通过键盘给二维整型数组a赋值。
for (i=0;i<N;i++)
{
for (j=0;j<M;j++)
{
printf ("a[%d][%d]=",i,j);
scanf ("%d",&a[i][j]);
}
}
printf ("\n二维整型数组a:\n");
//利用双重循输出二维整型数组a,并给二维整型数组b赋值。
for (i=0;i<N;i++)
{
for (j=0;j<M;j++)
{
printf ("%-5d",a[i][j]);
b[j][i]=a[i][j];
}
printf ("\n");
}
printf ("\n二维整型数组b:\n");
//利用双重循输出二维整型数组b。
for (j=0;j<M;j++)
{
for (i=0;i<N;i++)
{
printf ("%-5d",b[j][i]);
}
printf ("\n");
}
printf ("\n");
return 0;
}
程序运行结果:

第 19 例
程序源码:
/*
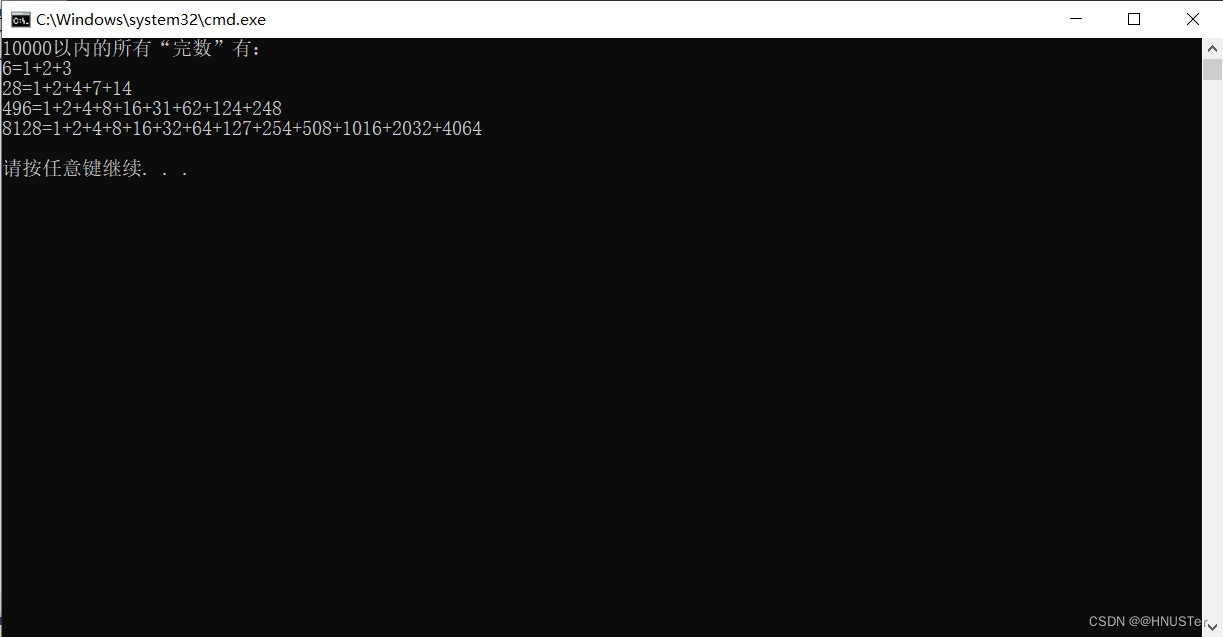
题目:一个数如果恰好等于它的因子之和,这个数就称为“完数”。例如6=1+2+3,编程找出10000以内的所有“完数”。
程序分析:请参照:C语言练习实例14,如下所示:
对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于(小于的时候,继续执行循环)n,则说明分解质因数的过程已经结束,另外 打印出即可。
(2)但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数n.重复执行第二步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
*/
#include<stdio.h>
#define N 10000
int main()
{
int i,j,k,n,sum;
int a[256];
printf ("10000以内的所有“完数”有:\n");
for(i=2;i<=N;i++)
{
sum=a[0]=1;
k=0;
for(j=2;j<=(i/2);j++)
{
if(i%j==0)
{
sum+=j;
a[++k]=j;
}
}
if(i==sum)
{
printf("%d=%d",i,a[0]);
for(n=1;n<=k;n++)
printf("+%d",a[n]);
printf("\n");
}
}
printf ("\n");
return 0;
}程序运行结果:
第 20 例
程序源码:
/*
题目:一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下,求它在第10次落地时,共经过多少米?第10次反弹多高?
程序分析:见下面注释。
*/
#include<stdio.h>
int main()
{
float h,s;
int i;
h=s=100.0;
h=h/2; //第一次反弹高度
for(i=2;i<=10;i++)
{
s=s+2*h;
h=h/2;
}
printf("第10次落地时,共经过%f米,第10次反弹高是%f米。\n",s,h);
printf ("\n");
return 0;
}程序运行结果: