leetcode每日一题复盘(10.2~10.8)

news2025/2/1 15:56:42

leetcode 347 前k个高频元素

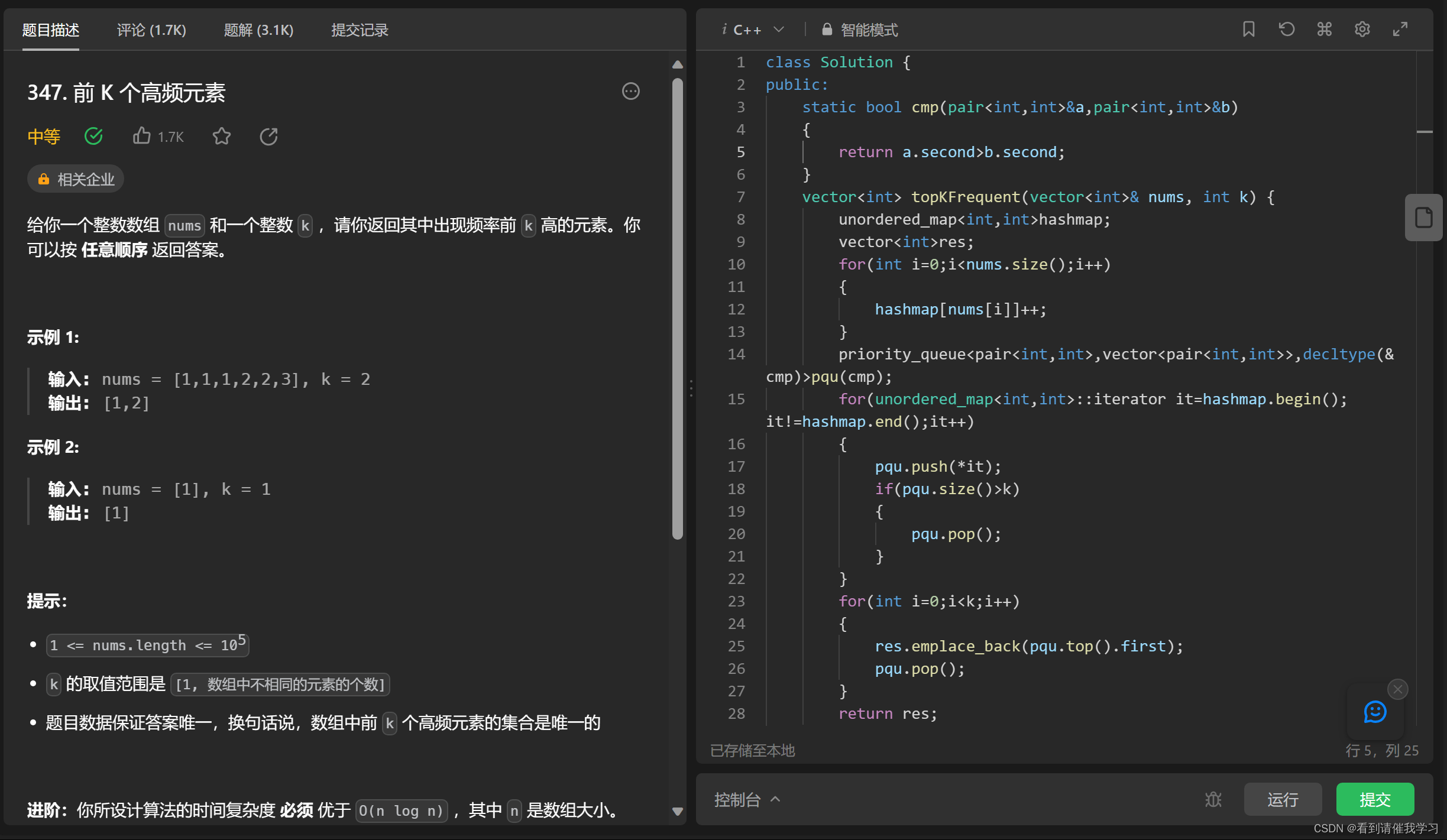
关键词:堆排序,优先队列,小根堆

这道题真没想出来怎么做,只能想到哈希统计数目,对优先队列还不是很熟悉,后来看了详解自己重写了一遍

主要思路是用哈希统计每个元素出现次数,再利用优先队列的性质创建小根堆(优先队列默认是从大到小排序,将是一个大根堆,因此需要重写比较函数cmp)

题目要求是前k个元素,因此我们维护一个大小为k的队列,每次插入元素队列自动排序将最小的排在堆顶,当数量>k时弹出堆顶元素,继续排序直到全部元素都遍历过

最后用vector存放堆中元素即可

为什么创建小根堆是a.second>b.second?

这个与优先队列的底层代码有关,其他数据结构a.second>b.second表示的是从大到小,只需要记住优先队列是相反的就可以了

leetcode 145 二叉树的后序遍历

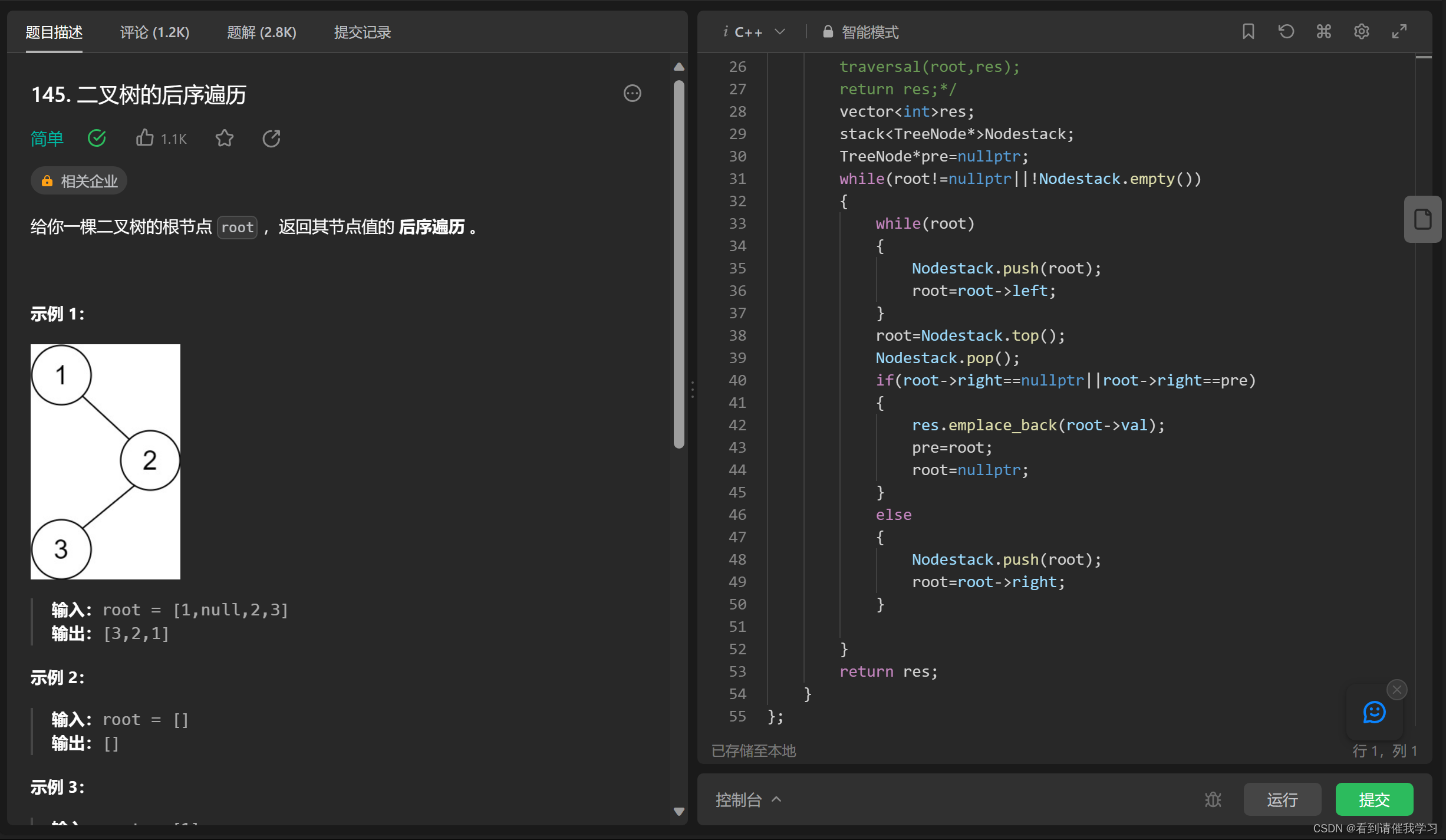
二叉树的后序遍历和144的前序遍历,94的中序遍历大同小异,这里就放一起当作一个题目来讲了

递归法

优点是代码简洁易写,但是效率差点,虽然时间复杂度都是O(n)

贴一个递归算法的代码,把递归顺序改一下就可以是其他遍历了

 void traversal(TreeNode*node,vector<int>&v)
    {
        if(node==nullptr)
        {
            return;
        }
        traversal(node->left,v);
        traversal(node->right,v); 
        v.emplace_back(node->val);
    }
  vector<int> postorderTraversal(TreeNode* root) {
        vector<int>res;
        traversal(root,res);
        return res;
}

迭代法

递归是隐式地调用栈,而迭代法就是显式地调用栈,将调用栈的过程以代码呈现出来

前序遍历

也就是我们的说的根左右,因为根在前,所以我们在遍历到根的时候就可以把根处理了(结果数组中插入根的值,不着急弹出根因为后面还要从根的右子树进行遍历)

先将根入栈,然后一直其根的左子树入栈,直到左子树为空就换成在右子树遍历,右子树遍历完后将根弹出,完成一个树遍历

 vector<int> preorderTraversal(TreeNode* root) {
        vector<int>res;
        stack<TreeNode*>Nodestack;
        while(root!=nullptr||!Nodestack.empty())
        {
            while(root)
            {
                Nodestack.push(root);
                res.emplace_back(root->val);
                root=root->left;
            }
            root=Nodestack.top()->right;
            Nodestack.pop();

        }
        return res;
    }

后序遍历

后序是左右根,因此根要放到最后才处理(也就是说,根最后才加入结果数组)

先将根的左子树全部入栈,直到root为空,此时将栈顶(左边最后一个根)设为root,再遍历其右子树,如果右子树为空,则可以将根加入结果数组中了

vector<int> postorderTraversal(TreeNode* root) {
        vector<int>res;
        stack<TreeNode*>Nodestack;
        TreeNode*pre=nullptr;
        while(root!=nullptr||!Nodestack.empty())
        {
            while(root)
            {
                Nodestack.push(root);
                root=root->left;
            }
            root=Nodestack.top();
            Nodestack.pop();
            if(root->right==nullptr||root->right==pre)
            {
                res.emplace_back(root->val);
                pre=root;
                root=nullptr;
            }
            else
            {
                Nodestack.push(root);
                root=root->right;
            }

        }
        return res;
    }

当然也有一种方法,可以将前序的遍历顺序换一下再reverse结果数组,就可以将前序遍历变成后序遍历

中序遍历

中序遍历的算法和前序遍历差不多,不过是根的处理时间换了一下

先遍历完左子树,再将根处理,再遍历右子树

vector<int> inorderTraversal(TreeNode* root) {
        vector<int>res;
        stack<TreeNode*>Nodestack;
        while(root!=nullptr||!Nodestack.empty())
        {
            while(root)
            {
                Nodestack.push(root);
                root=root->left;
            }
            root=Nodestack.top();
            res.emplace_back(root->val);
            Nodestack.pop();
            root=root->right;
           
        }
        return res;
    }