在【R: R package安装的几种方式】【R: R版本更新及R包迁移（详细步骤）】两篇文章中介绍过R包的常见安装方式，以及在不同R版本中如何进行迁移。

本篇主要介绍如何查看R包的默认安装位置，以及如何修改R包的安装位置。

一、R包安装位置查看

利用代码 “.libPaths()” 查看已安装R包在电脑上的存储位置（图1），可以看出笔者安装的R包存在两个存储位置， “C:/Users/hp/AppData/Local/R/win-library/4.3” 及 “D:/Program Files/R/R-4.3.1/library”。

> .libPaths()
[1] "C:/Users/hp/AppData/Local/R/win-library/4.3"
[2] "D:/Program Files/R/R-4.3.1/library" 

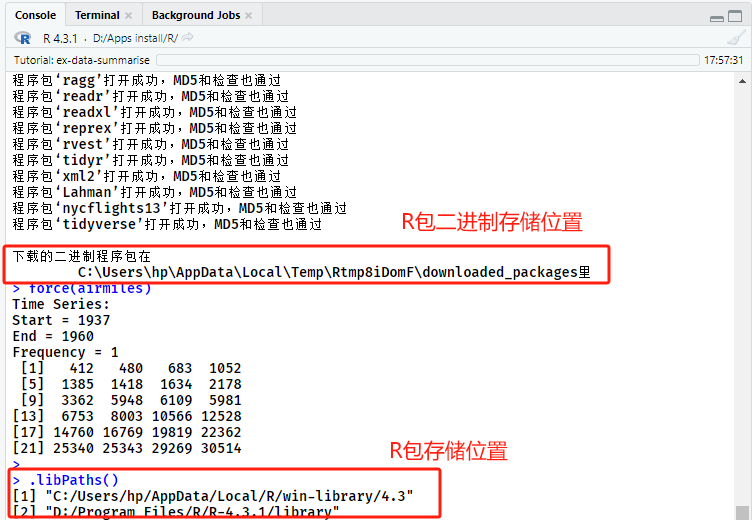
图1 R包安装及安装位置

二、已安装R包查询

利用代码 “library()” 查看已安装R包（图2），对应于图1R包安装位置，运行代码后，会在RStudio脚本编辑器中弹出新页面，分别显示 “C:/Users/hp/AppData/Local/R/win-library/4.3” 及 “D:/Program Files/R/R-4.3.1/library”两个安装路径下所有已安装的R包。

library()

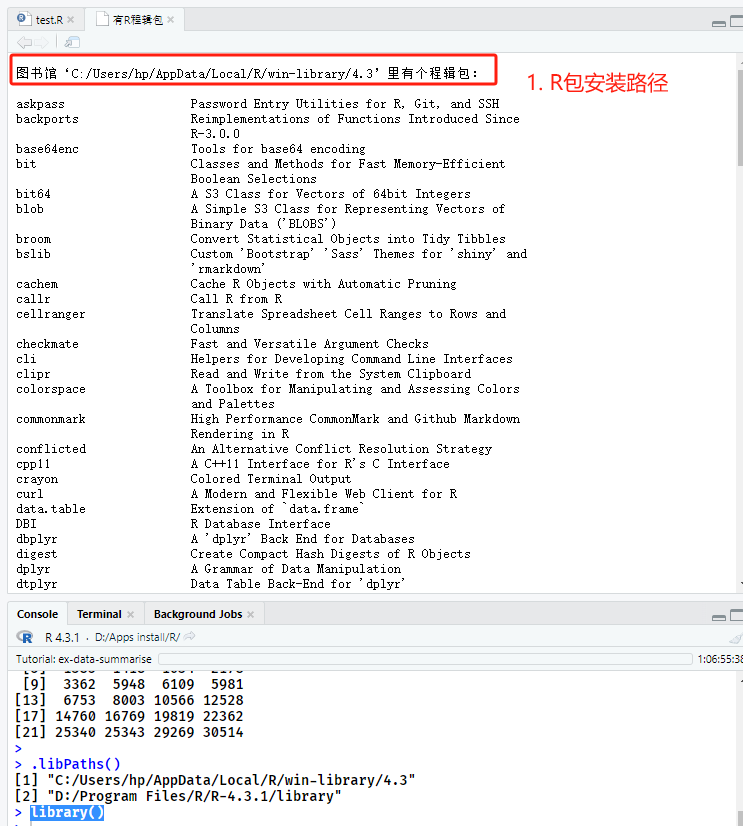
图2 不同路径下已安装R包

三、R包安装位置修改

利用代码 “.libPaths(“D:/Program Files/R/R-4.3.1/library”)” 修改R包安装位置。

.libPaths("D:/Program Files/R/R-4.3.1/library")

但在安装R包时提醒图3的问题，查阅资料后，可能原因如下：

• 使用管理员运行RStudio
• 防火墙导致

参考链接：
‘1. lib = “C:/Users/xxx/Documents/R/win-library/4.0”’ is not writable
‘2. lib = “C:/Users/xxx/Documents/R/win-library/4.0”’ is not writable

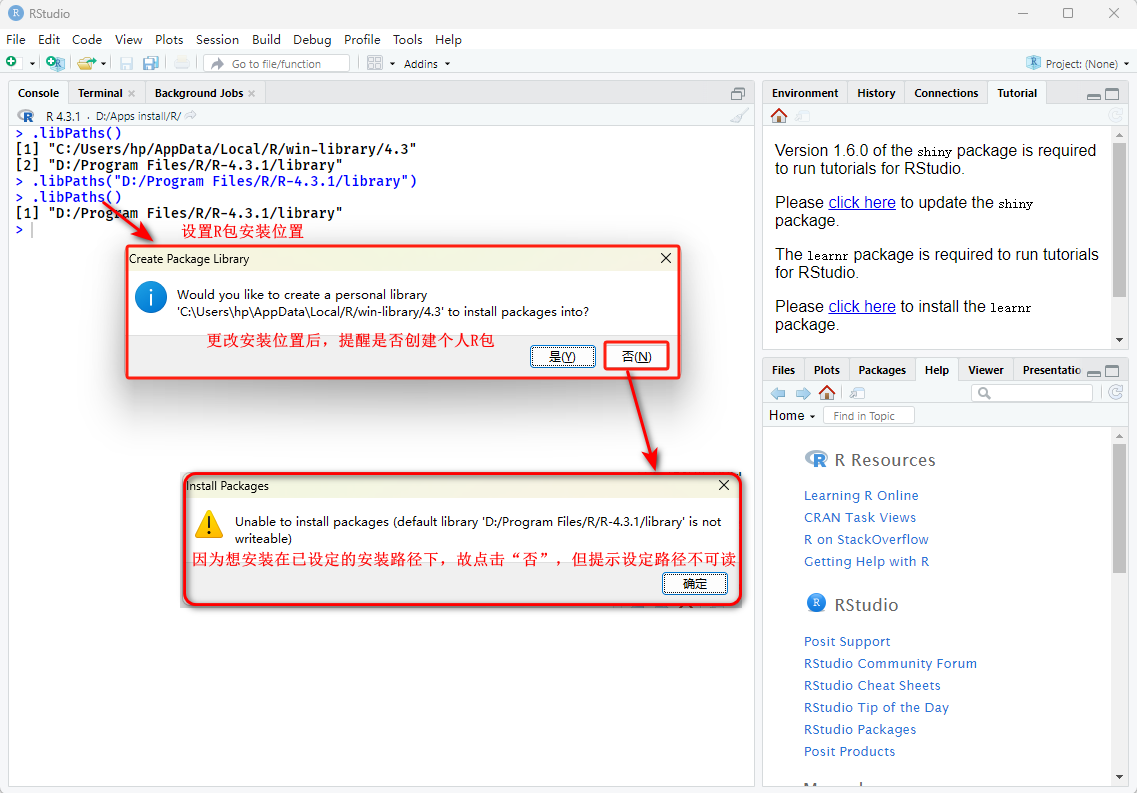
图3 R包安装位置不可读取

解决办法：
根据上述链接中的提示，关闭RStudio，以管理员身份重新打开RStudio，再次利用上述代码更改R包安装路径后，如图4所示，可以正常在设定路径下安装R包。

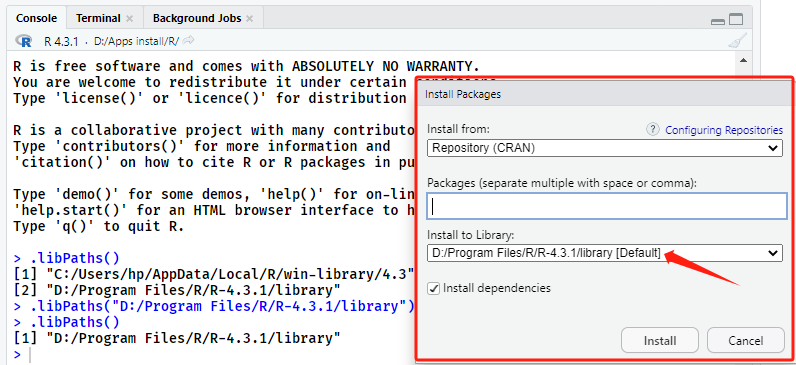
图4 R包安装路径修改成功

注：
这种方式只能临时修改R包安装位置，在重启RStudio后，会恢复到默认的R包安装路径。

四、R包安装位置永久修改

如图1所示，R包在下载安装时有两个位置，一个是默认创建的二进制包的下载地址，在C盘Users文件夹的downloaded_packages中；另一个是R包的具体安装地址。

destdir()参数是指定二进制压缩包下载位置的元素。由于“destdir()参数”是“install packages()函数”中的参数，在不对其进行设定时，会默认被放在C盘临时会话的downloaded_packages中。

lib()参数是指定二进制压缩包安装位置的元素。“lib()参数”是“install packages()函数”中的参数，在不对其进行设定时，会默认安装在.libPath()的第一个路径下（图1）。

故利用以下代码可对R包安装路径进行修改：

install.packages("R包名称",destdir = "二进制包存储路径",lib = "R包存储路径")

通常情况下，R包安装位置可以不用改，因为C盘文件夹的downloaded_packages在关闭R或RStudio时会自动删除下载的二进制压缩包，无需担心R包下载过多会影响C盘容量。
故实际情况下，可以设置**.libPaths()**即可，具体参照：三、R包安装位置修改。

但若仍想永久修改R包的默认安装路径，需要对配置文件进行修改。具体可参考如下链接中的内容：

• 自定义R函数包安装位置，专门解决R软件更新后所有R包要重装的Bug
• Rstudio 如何更改install.package安装包目录
• R语言中如何更改R包安装路径

参考内容：
R语言修改下载安装包install.package的默认存储位置