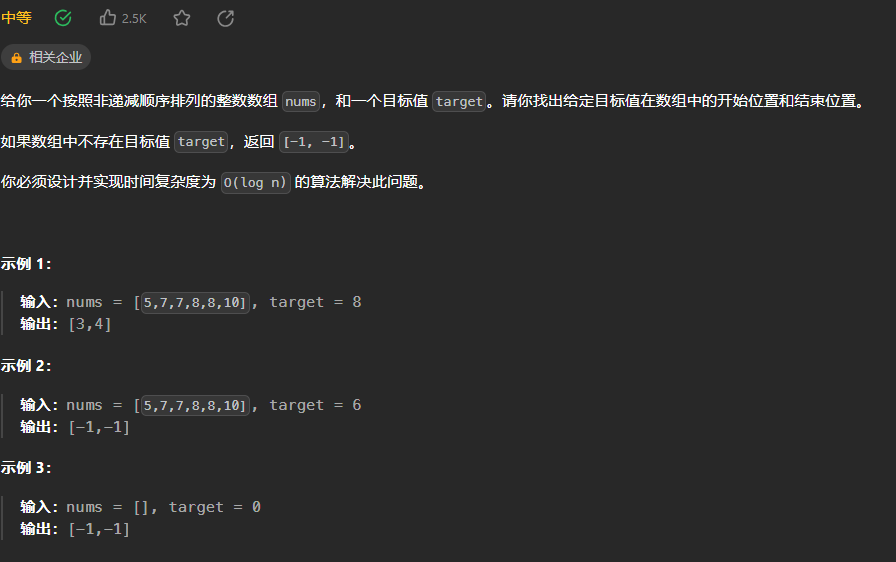
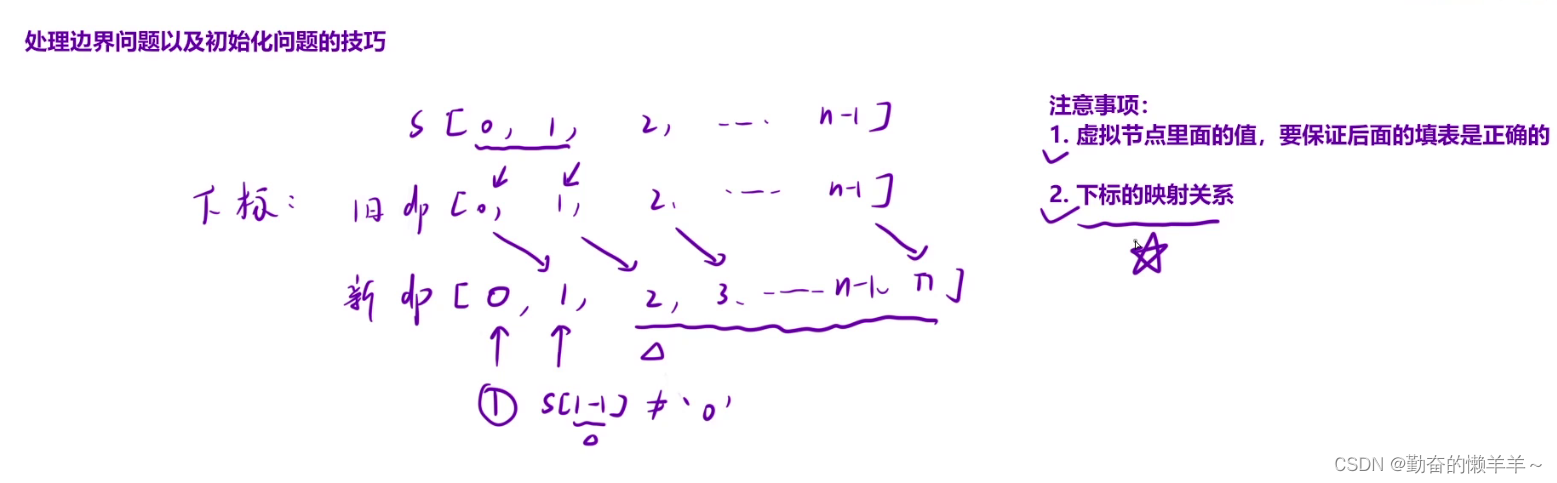解题步骤：

参考代码：

未优化的代码：

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {

        //计划数
        int len=group.size();
        
        //每一维都多开一行空间
        vector<vector<vector<int>>> dp(len+1,vector<vector<int>>(n+1,vector<int>(minProfit+1)));
        
        //初始化
        for(int j=0;j<=n;j++)
        {
            dp[0][j][0]=1;
        }

        //填表
        for(int i=1;i<=len;i++)
        {
            //记得从0开始
            for(int j=0;j<=n;j++)
            {
                //记得从0开始
                for(int k=0;k<=minProfit;k++)
                {
                    //状态转移方程
                    dp[i][j][k]+=dp[i-1][j][k];
                    if(j>=group[i-1])
                    {
                        //max(0,k-profit[i-1])非常重要
                        dp[i][j][k]=(dp[i][j][k]+dp[i-1][j-group[i-1]][max(0,k-profit[i-1])])%(1000000000+7);
                    }
                }
            }
        }

        return dp[len][n][minProfit];
    }
};

优化后的代码：

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
        //计划数
        int len=group.size();
        
        vector<vector<int>> dp(n+1,vector<int>(minProfit+1));
        
        //初始化
        for(int j=0;j<=n;j++)
        {
            dp[j][0]=1;
        }

        //填表
        for(int i=1;i<=len;i++)
        {
            //记得从大到小遍历
            for(int j=n;j>=group[i-1];j--)
            {
                //记得从大到小遍历
                for(int k=minProfit;k>=0;k--)
                {
                    //状态转移方程
                    dp[j][k]=(dp[j][k]+dp[j-group[i-1]][max(0,k-profit[i-1])])%(1000000000+7);
                }
            }
        }
        //返回值
        return dp[n][minProfit];
    }
};

你学会了吗？？？