简要介绍一下单调队列和优先级队列的不同 

1. 元素顺序的处理：单调队列中，元素的顺序是单调的，也就是说，队列中的元素按照特定的单调性（递增或递减）排列。这种特性使得单调队列在处理一些问题时非常高效，例如寻找滑动窗口中的最大值或最小值。优先队列则根据元素的优先级进行排序，优先级高的元素先出队。优先队列并不保证元素的单调性。
2. 入队和出队的操作：在单调队列中，元素可以从队尾入队，但出队操作只能在队首进行。这是因为单调队列需要保持其单调性，所以新加入的元素需要放在合适的位置以维持这种单调性。优先队列则允许元素从任意位置入队，出队操作则总是发生在优先级最高的元素上。
3. 队列长度：单调队列的长度取决于输入数据的合法性，如果输入数据不满足单调性要求，那么队列长度就可能为0。而优先队列的长度则始终与输入数据的数量等同，因为所有输入数据都会被放入队列中，只是出队的顺序会根据优先级有所不同。

更详细的题解和思路:代码随想录 (programmercarl.com)

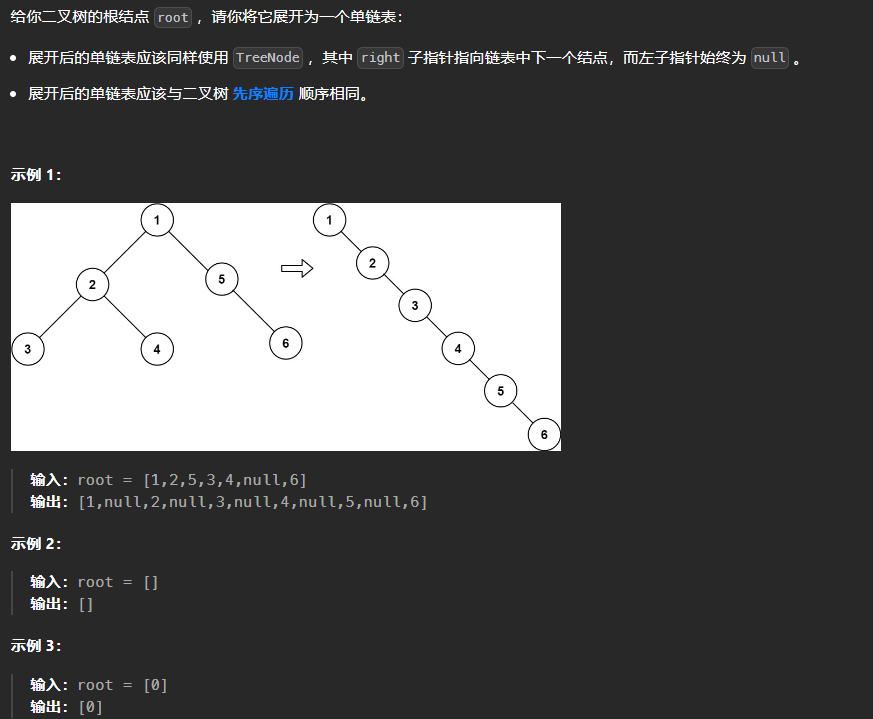
LeetCode T239 滑动窗口的最大值

题目链接:239. 滑动窗口最大值 - 力扣（LeetCode）

题目思路

这道题有点难度,我们如果使用暴力求解的话是跑不过的,暴力方式就是遍历全部的数组,再遍历每K个元素的滑动窗口,分别找出最大值放入返回数组,这里我们不使用这个方式.

我们使用单调队列而不是优先级队列

因为优先级队列只能将最大的元素选出来,而下一步操作

1.创建单调队列,定义add,peek,poll方法

poll方法:如果移除元素等于队列的出口元素,弹出该元素

add方法:如果队尾元素比传入元素小,删除该元素,保证前方元素都大于我要传入的元素,从而保证单调队列的单调性

peek方法:因为单调队列维护了队头的最大元素,peek用来返回队头元素

2.实现函数

首先创建单调队列,先将前k个元素传入单调队列,获取其最大值,对k到数组结束的元素进行以下处理,先poll前k个元素,加入新的元素,比较得到最大值,最后返回最大值数组即可.

代码实现

class MyQue{
    Deque<Integer> que = new LinkedList<>();
    void poll(int val)
    {
        if(!que.isEmpty() && val == que.peek())
        {
            que.poll();
        }

    }
    void  add(int val)
    {
        while(!que.isEmpty() && val>que.getLast())
        {
            que.removeLast();
        }
        que.add(val);

    }
    int peek()
    {
        return que.peek();
    }
}


class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length == 1)
        {
            return nums;
        }
        MyQue que = new MyQue();
        int len = nums.length;
        int num = 0;
        int[] res = new int[len-k+1];
        for(int i = 0;i<k;i++)
        {
            que.add(nums[i]);
        }
        res[num++] = que.peek();
        for(int i = k;i<len;i++)
        {
            que.poll(nums[i-k]);
            que.add(nums[i]);
            res[num++] = que.peek(); 
        }
        return res;
        
    }
}

LeetCode T347 前K个高频元素

题目链接:347. 前 K 个高频元素 - 力扣（LeetCode）

题目思路

首先创建一个map,key用来放置元素,value用来存放出现频率,这题我们就用到了优先级队列了,因为我们想用低于快排的时间复杂度解决问题,我们就只能使用大顶堆或小顶堆的数据结构,维护一个k个元素的堆来解决问题,最后将前k个元素依次pop出来即可.(这里为了简化代码使用了lambda表达式)

代码实现

class Solution {
    //解法1：基于大顶堆实现
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        //在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2)->pair2[1]-pair1[1]);
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){//大顶堆需要对所有元素进行排序
            pq.add(new int[]{entry.getKey(),entry.getValue()});
        }
        int[] ans = new int[k];
        for(int i=0;i<k;i++){//依次从队头弹出k个,就是出现频率前k高的元素
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}

 //解法2：基于小顶堆实现
    public int[] topKFrequent2(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
        for(int num:nums){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        //在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);
        for(Map.Entry<Integer,Integer> entry:map.entrySet()){//小顶堆只需要维持k个元素有序
            if(pq.size()<k){//小顶堆元素个数小于k个时直接加
                pq.add(new int[]{entry.getKey(),entry.getValue()});
            }else{
                if(entry.getValue()>pq.peek()[1]){//当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                    pq.poll();//弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
                    pq.add(new int[]{entry.getKey(),entry.getValue()});
                }
            }
        }
        int[] ans = new int[k];
        for(int i=k-1;i>=0;i--){//依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
            ans[i] = pq.poll()[0];
        }
        return ans;

简化版代码(避免一些api) 

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 优先级队列，为了避免复杂 api 操作，pq 存储数组
        // lambda 表达式设置优先级队列从大到小存储 o1 - o2 为从大到小，o2 - o1 反之
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
        int[] res = new int[k]; // 答案数组为 k 个元素
        Map<Integer, Integer> map = new HashMap<>(); // 记录元素出现次数
        for(int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
        for(var x : map.entrySet()) { // entrySet 获取 k-v Set 集合
            // 将 kv 转化成数组
            int[] tmp = new int[2];
            tmp[0] = x.getKey();
            tmp[1] = x.getValue();
            pq.offer(tmp);
            if(pq.size() > k) {
                pq.poll();
            }
        }
        for(int i = 0; i < k; i ++) {
            res[i] = pq.poll()[0]; // 获取优先队列里的元素
        }
        return res;
    }
}