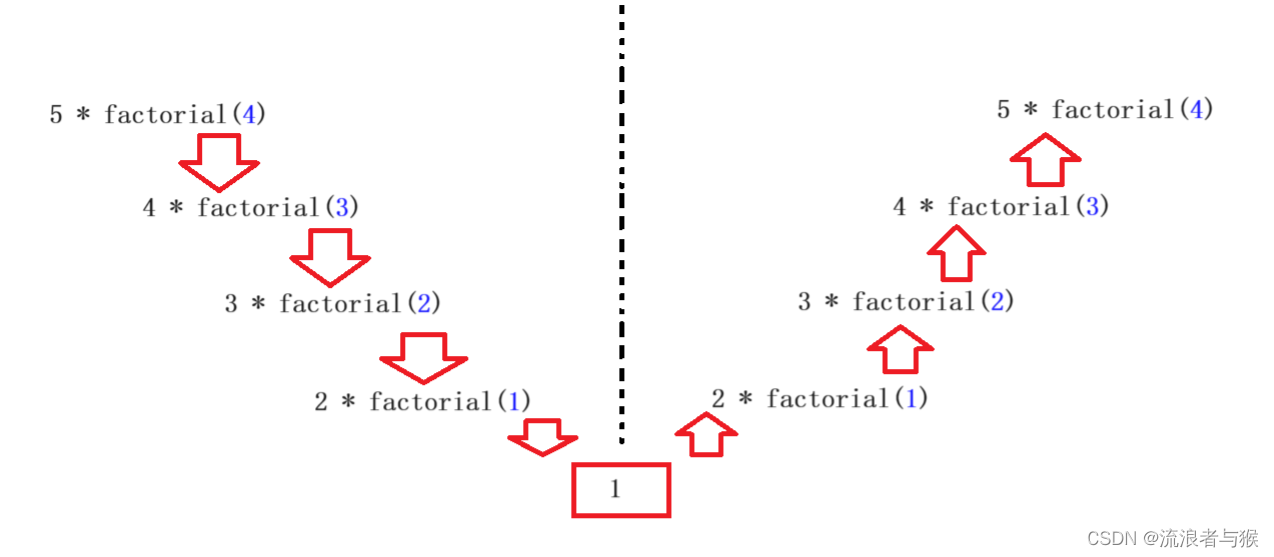
动态规划算法框架:
- 问题结构分析
- 递推关系建立
- 自底向上计算
- 最优方案追踪
背包问题
输入:
- n n n个商品组成的集合 O O O,每个商品有两个属性 v i v_i vi和 p i p_i pi,分别表示体积和价格
- 背包容量 C C C
输出:
- 求解一个商品子集 S ⊆ O S\subseteq O S⊆O
直观策略
- 策略1:按商品价格由高到低排序,优先挑选价格高的商品
- 策略2:按商品体积由小到大排序,优先挑选体积小的商品
- 策略3:按商品价值与体积的比由高到低排序,优先挑选比值高的商品
这三种策略都不能保证得到最优解
蛮力枚举
- 枚举所有商品组合: 2 n − 1 2^n-1 2n−1种情况
- 检查体积约束
递归函数KnapsackSR(h,i,c):
- 在第 h h h个到第 i i i个商品中,容量为 c c c时最优解
- 选择啤酒: K n a p s a c k S R ( 1 , 4 , 3 ) + 24 KnapsackSR(1,4,3)+24 KnapsackSR(1,4,3)+24
- 不选啤酒: K n a p s a c k S R ( 1 , 4 , 13 ) KnapsackSR(1,4,13) KnapsackSR(1,4,13)
伪代码:
输入:商品集合{h,...,i},背包容量c
输出:最大总价格P
if c<0 then
| return 0
end
if i <= h-1 then
| return 0
end
P1 <- KnapsackSR(h,i-1,c-vi)
P2 <- KnapsackSR(h,i-1,c)
P <- max(P1+pi,P2)
return P
重复求解大量子问题: O ( 2 n ) O(2^n) O(2n)
动态规划
从蛮力枚举到带备忘递归
- 优化子问题解,避免重复计算
构造备忘录P[i,c],P[i,c]表示在前i个商品中选择,背包容量为c时的最优解
输入:商品集合{h,...,i},背包容量c
输出:最大总价格P
if c<0 then
| return 0
end
if i <= h-1 then
| return 0
end
if P[i,c]!=NULL then
| return P[i,c]
end
P1 <- KnapsackMR(h,i-1,c-vi)
P2 <- KnapsackMR(h,i-1,c)
P[i,c] <- max(P1+pi,P2)
return P[i,c]
递推求解
容量为0时:
P
[
i
,
0
]
=
0
P[i,0]=0
P[i,0]=0
没有商品时:
P
[
0
,
c
]
=
0
P[0,c]=0
P[0,c]=0
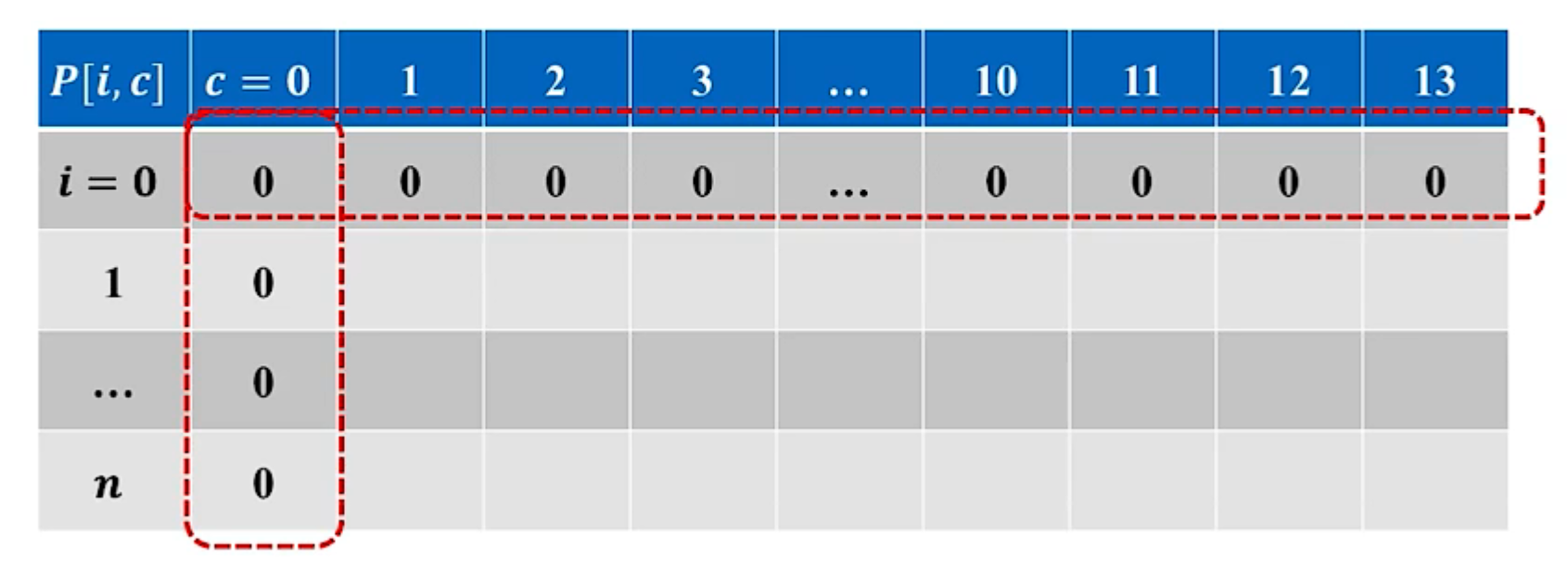
确定计算顺序:
- 按从左往右、从上到下的顺序计算
问题:如何确定选取了哪些商品
- 记录决策过程:KaTeX parse error: {align} can be used only in display mode.
回溯解决方案:
- 倒序判断是否选择商品
- 根据选择结果,确定最优子问题
伪代码:
输入:商品集合{h,...,i},背包容量c
输出:最大总价格P
//初始化,创建二维数组P和Rec
for i <- 0 to C do
| P[0,i] <- 0
end
for i <- 0 to n do
| P[i,0] <- 0
end
//求解表格
for i <- 1 to n do
| for c <- 1 to C do
| | if v[i]<=c and p[i]+P[i-1,c-v[i]]>P[i-1,c] then
| | | P[i,c]=p[i]+P[i-1,c-v[i]]
| | | Rec[i,c] <- 1
| | end
| | else
| | | P[i,c] <- P[i-1,c]
| | | Rec[i,c] <- 0
| | end
| end
end
时间复杂度:
O
(
n
⋅
C
)
O(n\cdot C)
O(n⋅C)
上面带备忘递归和递推求解的方法都属于动态规划:
- 带备忘递归:自顶向下
- 递推求解:自底向上
最优子结构性质:
- 问题的最优解由相关子问题最优解组合而成
- 子问题可以独立求解
动态规划与分而治之的区别:
- 动态规划:重叠子问题
- 分而治之:独立子问题
最大子数组
问题结构分析:
- 给出问题表示: D [ i ] D[i] D[i]为以 X [ i ] X[i] X[i]开头的最大子数组和
- 明确原始问题 S m a x = m a x { D i } S_{max}=max\{D_i\} Smax=max{Di}
递推关系建立:
- 情况一: D [ i + 1 ] > 0 D[i+1]>0 D[i+1]>0,则 D [ i ] = X [ i ] + D [ i + 1 ] D[i]=X[i]+D[i+1] D[i]=X[i]+D[i+1]
- 情况二: D [ i + 1 ] ≤ 0 D[i+1]\leq0 D[i+1]≤0,则 D [ i ] = X [ i ] D[i]=X[i] D[i]=X[i]
自底向上计算:
- 初始化: D [ n ] = X [ n ] D[n]=X[n] D[n]=X[n]
- 递推公式:KaTeX parse error: {align} can be used only in display mode.
记录决策过程:
- 构造追踪数组 R e c [ 1.. n ] Rec[1..n] Rec[1..n]
- 情况一:结尾相同,则 R e c [ i ] = R e c [ i + 1 ] Rec[i]=Rec[i+1] Rec[i]=Rec[i+1]
- 情况二:结尾不同,则 R e c [ i ] = i Rec[i]=i Rec[i]=i
最优方案追踪:
- 从子问题中查找最优解
- 最大子数组开头位置: i i i
- 最大子数组结尾位置: R e c [ i ] Rec[i] Rec[i]
伪代码:
输入:数组X,数组长度n
输出:最大子数组和Smax,子数组起止位置l,r
//初始化
D[n] <- X[n]
Rec[n] <- n
//动态规划
for i <- n-1 to 1 do
| if D[i+1]>0 then
| | D[i] <- X[i]+D[i+1]
| | Rec[i] <- Rec[i+1]
| end
| else
| | D[i] <- X[i]
| | Rec[i] <-i
| end
end
//查找解
Smax <- D[1]
for i <- 2 to n do
| if Smax<D[i] then
| | Smax<-D[i]
| | l <- i
| | r <- Rec[i]
| end
end
return Smax,l,r
最长公共子序列
子序列:将给定序列中零个或多个元素去掉后所得的结果
蛮力枚举
枚举所有子序列
可能存在最优子结构和重叠子问题
动态规划
问题结构分析:
- 给出问题表示: C [ i , j ] C[i,j] C[i,j]表示 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]的最长公共子序列长度
递推关系建立:分析最优子结构
- 考察末尾字符:
- 情况1: x i ≠ y j x_i\neq y_j xi=yj时, C [ i , j ] = m a x { C [ i , j − 1 ] , C [ i − 1 , j ] } C[i,j]=max\{ C[i,j-1],C[i-1,j] \} C[i,j]=max{C[i,j−1],C[i−1,j]}
- 情况2: x i = y j x_i= y_j xi=yj时, C [ i , j ] = C [ i − 1 , j − 1 ] + 1 C[i,j]= C[i-1,j-1]+1 C[i,j]=C[i−1,j−1]+1
自底向上计算:确定计算顺序
- 初始化: C [ i , 0 ] = C [ 0. j ] = 0 C[i,0]=C[0.j]=0 C[i,0]=C[0.j]=0//某序列长度为0时,最长公共子序列长度为0
- 递推公式:KaTeX parse error: {align} can be used only in display mode.
最优方案追踪:记录决策过程
- 构造追踪数组 r e c [ 1.. n ] rec[1..n] rec[1..n],记录子问题来源:KaTeX parse error: {align} can be used only in display mode.
伪代码:
输入:两个序列X,Y
输出:X和Y的最长公共子序列
n <- length(X)
m <- length(Y)
//初始化
新建二维数组C[n,m]和rec[n,m]
for i <- 0 to n do
| C[i,0] <-0
end
for j <- 0 to m do
| C[0,j] <- 0
end
//动态规划
for i <- 1 to n do
| for j <- 1 to m do
| | if Xi=Yj then
| | | C[i,j] <- C[i-1.j-1]+1
| | | rec[i,j] <- 'LU'
| | end
| | else if C[i-1,j]>=C[i,j-1] then
| | | C[i,j] <- C[i-1,j]
| | | rec[i,j] <- 'U'
| | end
| | else
| | | C[i,j] <- C[i,j-1]
| | | rec[i,j] <- 'L'
| | end
| end
end
return C,rec
时间复杂度: O ( n ⋅ m ) O(n\cdot m) O(n⋅m)
最长公共子串
子串:给定序列中零个或多个连续的元素组成的子序列
蛮力枚举
- 序列X和序列Y各选择一个位置
- 依次检查元素是否匹配:
- 元素相等则继续匹配
- 元素不等或某序列已达端点,匹配终止
可能存在最优子结构和重叠子问题。
动态规划
问题结构分析:
- 给出问题表示: C [ i , j ] C[i,j] C[i,j]表示 X [ 1.. i ] X[1..i] X[1..i]和 Y [ 1.. j ] Y[1..j] Y[1..j]中,以 x i x_i xi和 y j y_j yj结尾的最长公共子串 Z [ 1.. l ] Z[1..l] Z[1..l]的长度
递推关系建立:分析最优子结构
- KaTeX parse error: {align} can be used only in display mode.
自底向上计算:确定计算顺序
- 初始化: C [ i , 0 ] = C [ 0. j ] = 0 C[i,0]=C[0.j]=0 C[i,0]=C[0.j]=0//某序列长度为0时,最长公共子串长度为0
- 原始问题: p m a x = m a x { C [ i , j ] } p_{max}=max\{C[i,j]\} pmax=max{C[i,j]}
最优方案追踪:记录决策过程
- 最长公共子串末尾位置 p m a x p_{max} pmax
- 最长公共子串长度 l m a x l_{max} lmax
伪代码
输入:两个字符串X,Y
输出:X和Y的最长公共子串
//初始化
n <- length(X)
m <- length(Y)
新建二维数组C[n,m]
lmax <- 0
pmax <- 0
for i <- 0 to n do
| C[i,0] <- 0
end
for j <- 0 to n do
| C[0,j] <-0
end
//动态规划
for i <- 1 to n do
| for j <- 1 to m do
| | if Xi != Yj then
| | | C[i,j] <- 0
| | end
| | else
| | | C[i,j] <- C[i-1,j-1]+1
| | | if C[i,j] > lmax then
| | | | lmax <- C[i,j]
| | | | pmax <- i
| | | end
| | end
| end
end
编辑距离问题
编辑操作:删除、插入、替换
递推关系建立:只操作
s
s
s串
- 删除: D [ i , j ] = D [ i − 1 , j ] + 1 D[i,j]=D[i-1,j]+1 D[i,j]=D[i−1,j]+1
- 插入: D [ i , j ] = D [ i , j − 1 ] + 1 D[i,j]=D[i,j-1]+1 D[i,j]=D[i,j−1]+1
- 替换:KaTeX parse error: {align} can be used only in display mode.
- 综合以上三种方式:KaTeX parse error: {align} can be used only in display mode.
- 最小编辑距离VS最长公共子序列:
- KaTeX parse error: {align} can be used only in display mode.
- KaTeX parse error: {align} can be used only in display mode.
自底向上计算:
- 初始化:
- D [ i , 0 ] = i D[i,0]=i D[i,0]=i//把长度为 i i i的串变为空串至少需要 i i i次删除操作
- D [ j , 0 ] = j D[j,0]=j D[j,0]=j//把空串变为长度为 j j j的串至少需要 j j j次插入操作
- 递推公式:
- KaTeX parse error: {align} can be used only in display mode.
最优方案追踪:
- 追踪数组 R e c Rec Rec,记录子问题来源
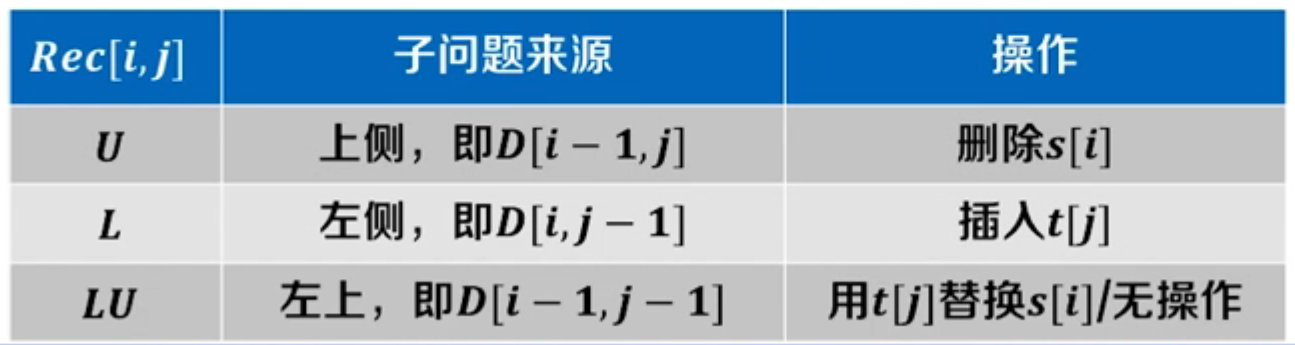
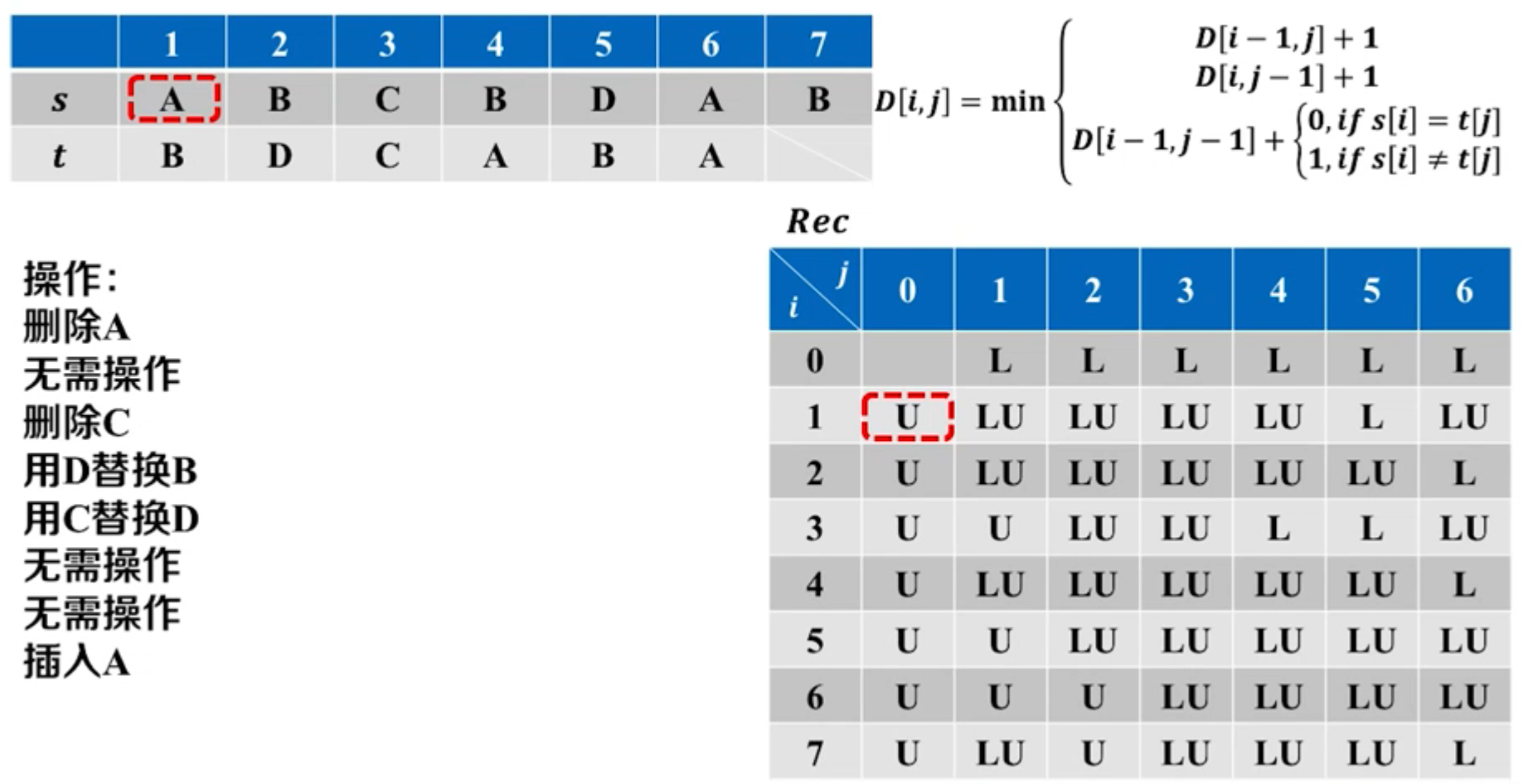
伪代码
输入:字符串s和t
输出:s和t的最小编辑距离
n <- length(s)
m <- length(t)
新建D[0..n,0..m],Rec[0..n,0..m]两个数组
//初始化
for i <- 0 to n do
| D[i,0] <- i
| Rec[i,0] <- 'U'
end
for j <- 0 to m do
| D[0,j] <- j
| Rec[0,j] <- 'L'
end
//动态规划
for i <- 1 to n do
| for j <- 1 to m do
| | c <- 0
| | if si!=tj then
| | | c <- 1
| | end
| | replace <- D[i-1,j-1]+c
| | delete <- D[i-1,j]+1
| | insert <- D[i,j-1]+1
| | if replace =min{replace,delete,insert} then
| | | D[i,j] <- D[i-1,j-1]+c
| | | Rec[i,j] <- 'LU'
| | end
| | else if insert = min{replace,delete,insert} then
| | | D[i,j] <- D[i,j-1]+1
| | | Rec[i,j] <- 'L'
| | end
| | else
| | | D[i,j] <- D[i-1,j]+1
| | | Rec[i,j] <- 'U'
| | end
| end
end
最优方案追踪-伪代码
输入:矩阵Rec,字符串s,t,索引位置i,j
输出:操作序列
if i=0 and j=0 then
| return NULL
end
if Rec[i,j]='LU' then
| Print-MED(Rec,s,t,i-1,j-1)
| if si=tj then
| | print '无需操作'
| end
| else
| | print '用tj代替si'
| end
end
else if Rec[i,j]='U' then
| Print-MED(Rec,s,t,i-1,j)
| print '删除si'
end
else
| Print-MED(Rec,s,t,i,j-1)
| print '插入tj'
end
钢条切割问题
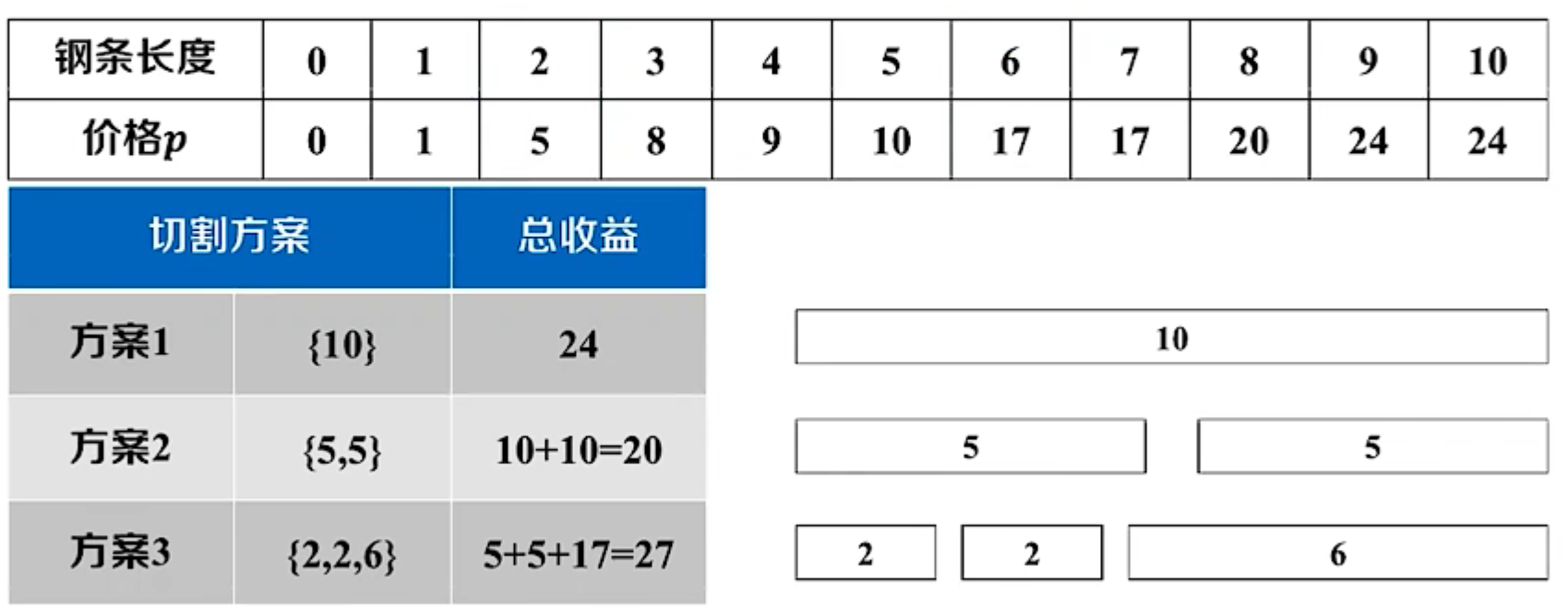
形式化定义
输入:
- 钢条长度 n n n
- 价格表 p l p_l pl:表示长度为 l l l的钢条价格
输出:
- 一组切割方案,令收益最大
问题简化
假设至多切割1次,枚举所有可能的切割位置:
- 不切: p [ 10 ] p[10] p[10]
- 切割: p [ i ] + p [ 10 − i ] p[i]+p[10-i] p[i]+p[10−i]
假设至多切割2次:
- 先将钢条切割一段
- 在剩余钢条中继续切割,剩余的问题变为至多切一刀的问题
原始问题不限制切割次数
- 可能存在最优子结构和重叠子问题
动态规划
问题结构分析:
- 给出问题表示: C [ j ] C[j] C[j]表示切割长度为 j j j的钢条可得的最大收益
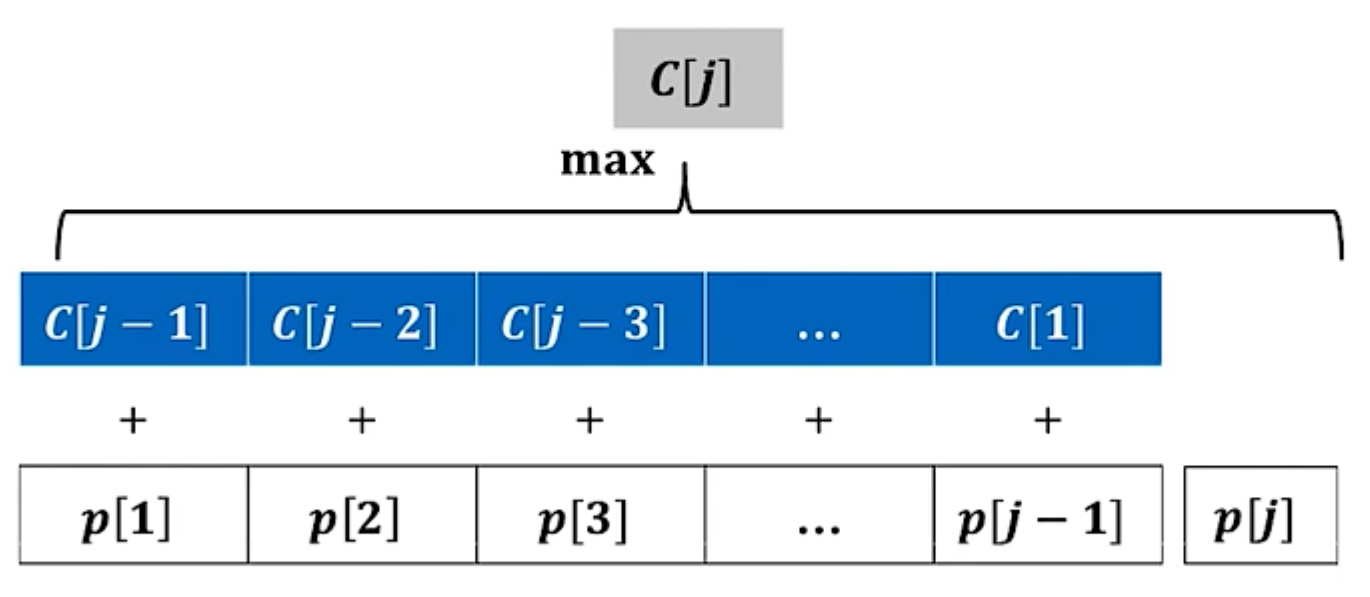
递推关系建立:
C
[
j
]
=
m
a
x
{
p
[
i
]
+
C
[
j
−
i
]
,
p
[
j
]
}
C[j]=max\{ p[i]+C[j-i],p[j] \}
C[j]=max{p[i]+C[j−i],p[j]}
自底向上计算:
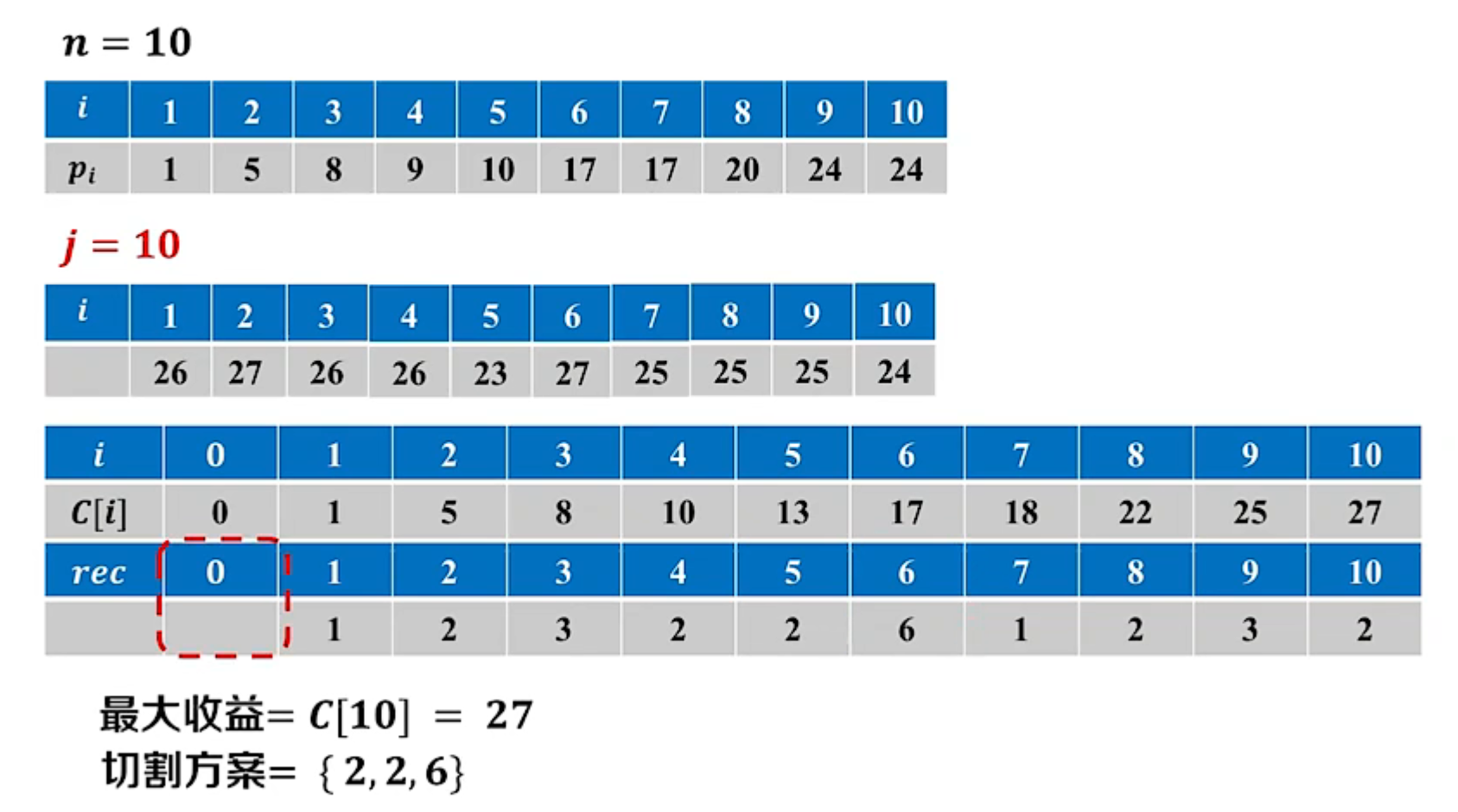
- 初始化: C [ 0 ] = 0 C[0]=0 C[0]=0//切割长度为0的钢条,总收益为0
- 递推公式: C [ j ] = m a x { p [ i ] + C [ j − i ] , p [ j ] } C[j]=max\{ p[i]+C[j-i],p[j] \} C[j]=max{p[i]+C[j−i],p[j]}
最优方案追踪:记录决策过程
- 构造追踪数组 r e c [ 1.. n ] rec[1..n] rec[1..n]
- r e c [ j ] rec[j] rec[j]:记录长度为 j j j的钢条的最优切割方案
伪代码
输入:钢条价格表p[1..n],钢条长度n
输出:最大收益C[n],钢条切割方案
//初始化
新建一维数组C[0..n],rec[0..n]
C[0] <- 0
//动态规划
for j <- 1 to n do
| q <- p[j]
| rec[j] <- j
| for i <- 1 to j-1 do
| | if q<p[i]+C[j-i] then
| | | q <- p[i]+C[j-i]
| | | rec[j] <- i
| | end
| end
| C[j] <- q
end
//输出最优方案
while n>0 do
| print rec[n]
| n <- n-rec[n]
end
时间复杂度为 O ( n 2 ) O(n^2) O(n2)
矩阵链乘法问题
矩阵乘法时间复杂度:
- 计算一个数字: q q q次标量乘法
- 共 p × r p\times r p×r个数字: Θ ( p q r ) \Theta(pqr) Θ(pqr)
三个矩阵相乘:
- ( U V ) W = U ( V W ) (UV)W=U(VW) (UV)W=U(VW)
- 新问题:矩阵乘法结合的顺序

n
n
n个矩阵相乘:
- 一系列矩阵按顺序排列
- 每个矩阵的行数=前一个矩阵的列数
- n n n个矩阵相乘也被称为矩阵链乘法
问题定义
输入:
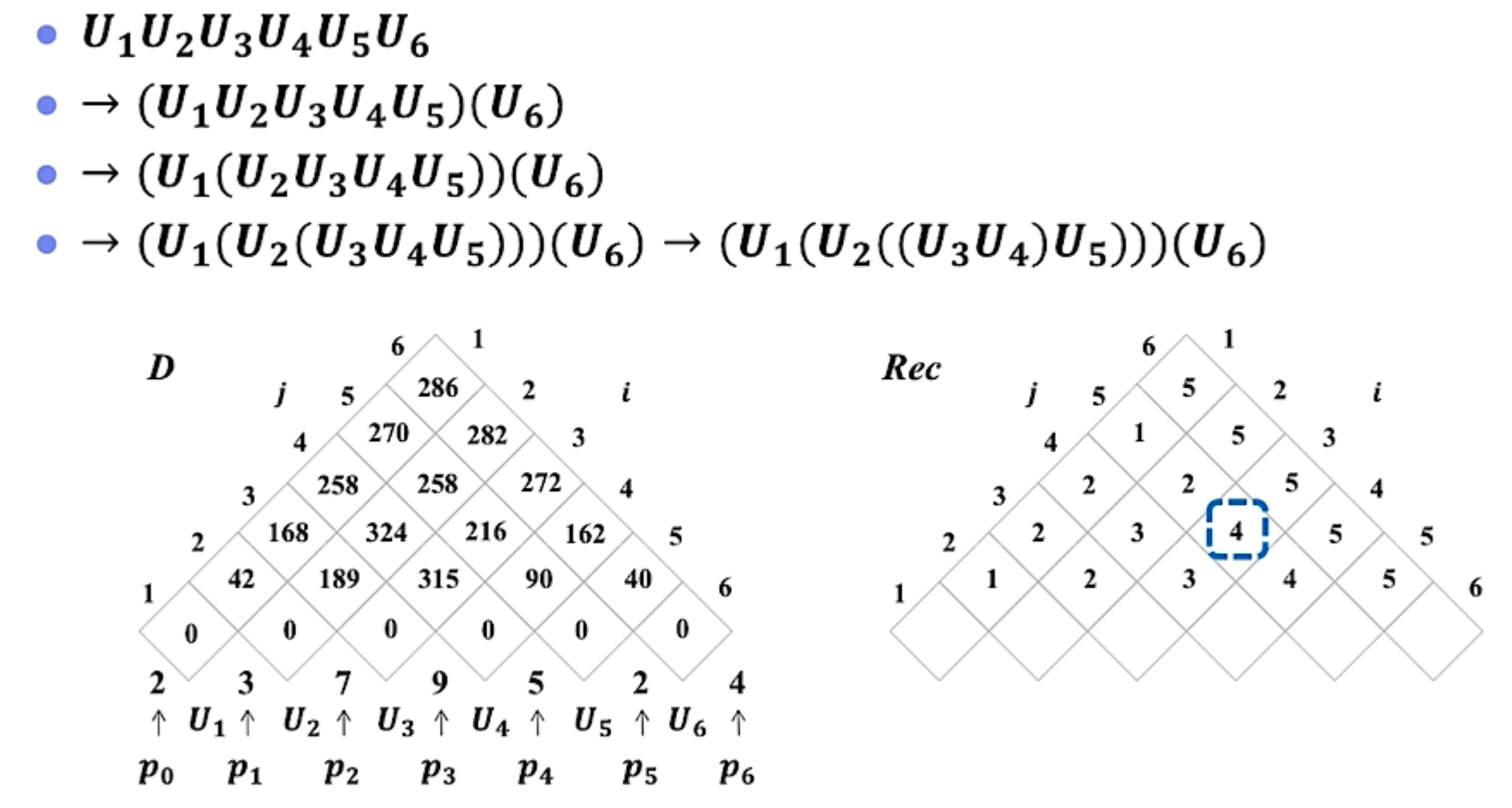
- n n n个矩阵组成的矩阵链 U 1.. n = < U 1 , U 2 , . . . , U n > U_{1..n}=<U_1,U_2,...,U_n> U1..n=<U1,U2,...,Un>
- 矩阵链 U 1.. n U_{1..n} U1..n对应的维度数分别为 p 0 , p 1 , . . . , p n p_0,p_1,...,p_n p0,p1,...,pn, U i U_i Ui的维度是 p i − 1 × p i p_{i-1}\times p_i pi−1×pi
输出:
- 找到一种加括号的方式,使得矩阵链标量乘法的次数最少
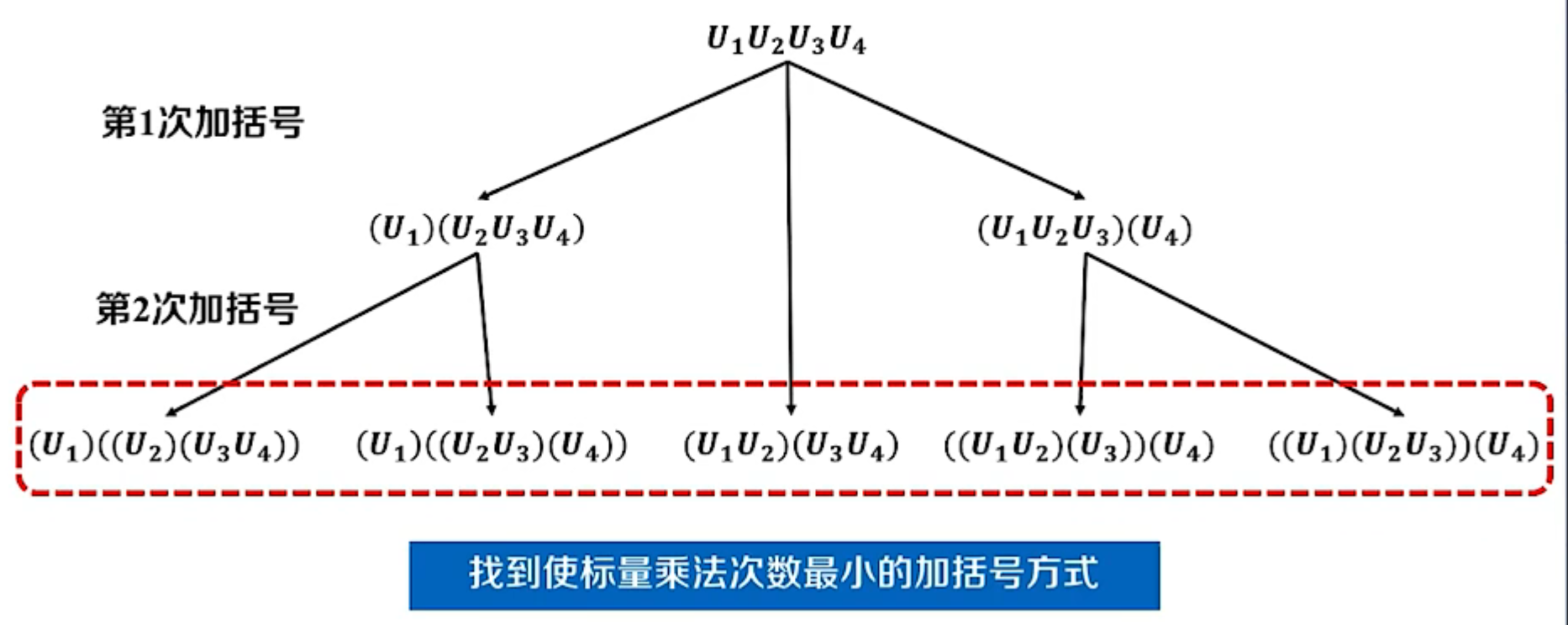
如何保证不遗漏最优分割位置:
- 枚举所有可能位置 i . . j − 1 i..j-1 i..j−1,共 j − i j-i j−i种
问题结构分析:
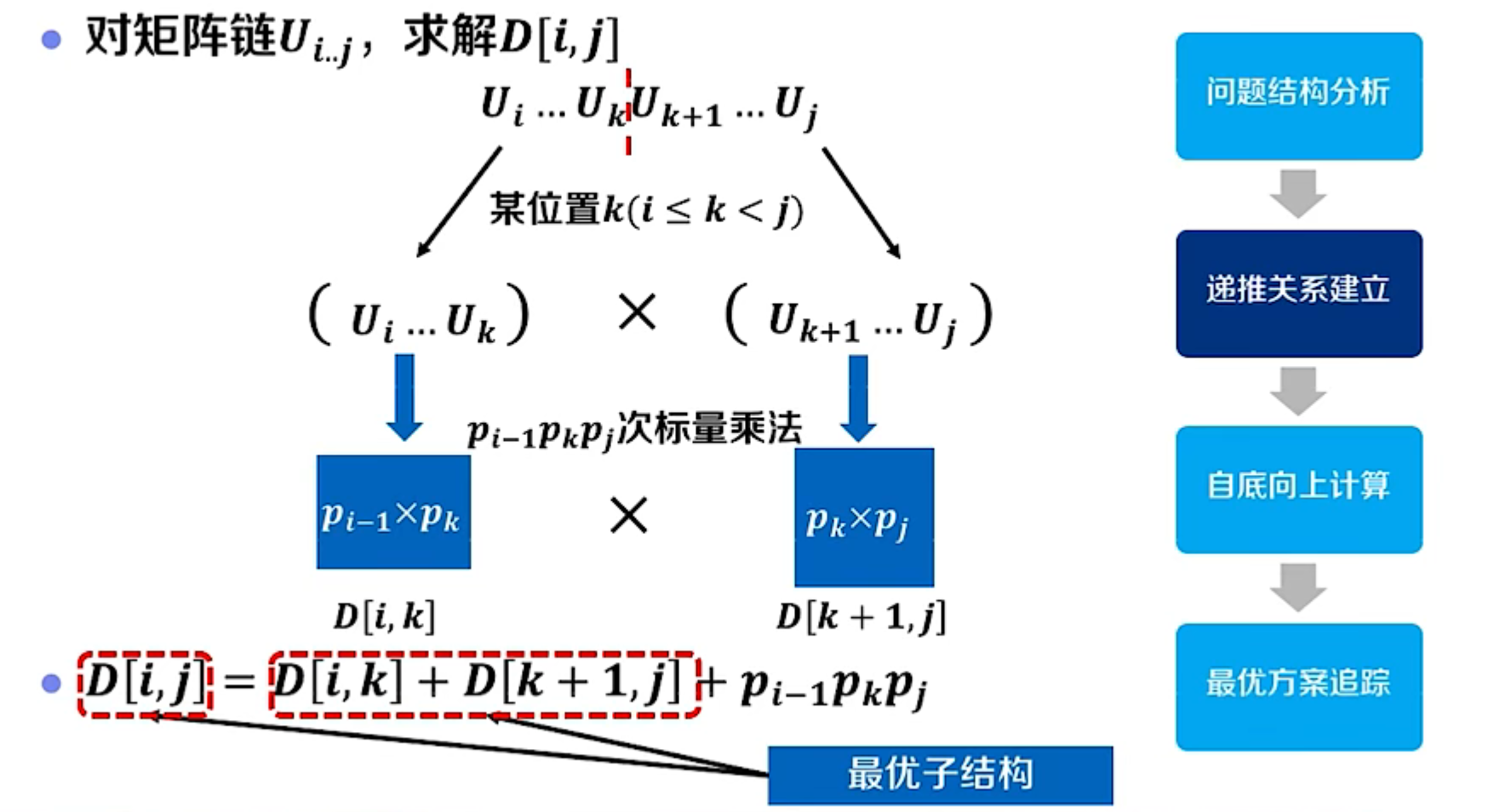
- 明确原始问题: D [ 1 , n ] D[1,n] D[1,n]表示计算矩阵链 U 1.. n U_{1..n} U1..n所需标量乘法的最小次数
递推关系建立:
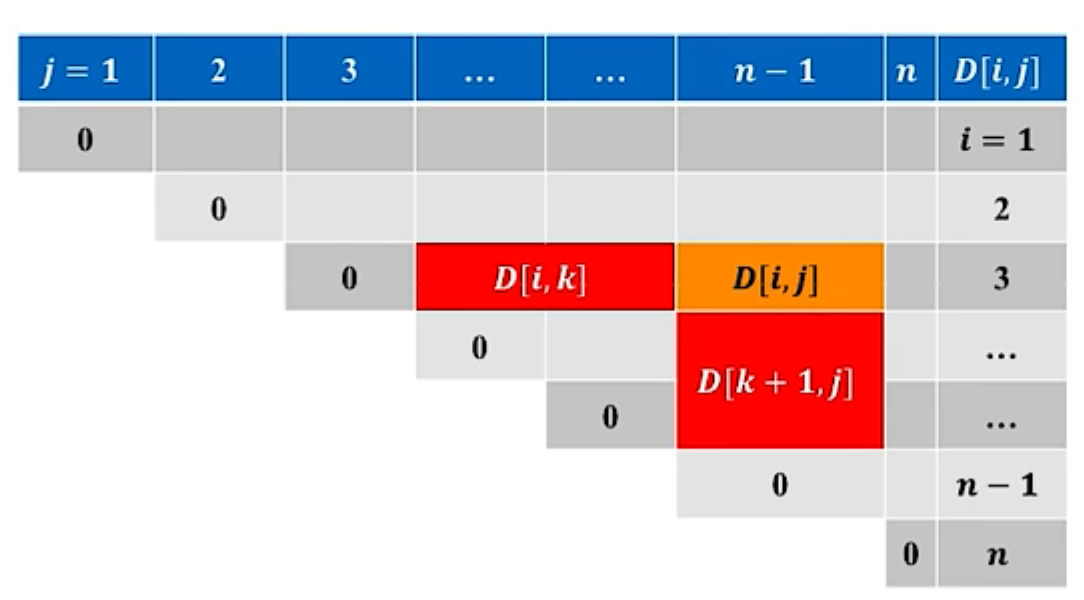
- 对每个位置 k ( i ≤ k ≤ j ) k(i\leq k\leq j) k(i≤k≤j): D [ i , j ] = D [ i , k ] + D [ k + 1 , j ] + p i − 1 p k p j D[i,j]=D[i,k]+D[k+1,j]+p_{i-1}p_kp_j D[i,j]=D[i,k]+D[k+1,j]+pi−1pkpj
- 枚举所有 k k k,得到递推式: D [ i , j ] = m i n ( D [ i , k ] + D [ k + 1 , j ] + p i − 1 p k p j ) D[i,j]=min(D[i,k]+D[k+1,j]+p_{i-1}p_kp_j) D[i,j]=min(D[i,k]+D[k+1,j]+pi−1pkpj)
自底向上计算:
- 初始化:
i
=
j
i=j
i=j时,矩阵链只有一个矩阵,乘法次数为
0。
最优方案追踪:
- 构造追踪数组 R e c [ 1.. n , 1.. n ] Rec[1..n,1..n] Rec[1..n,1..n]
- R e c [ i , j ] Rec[i,j] Rec[i,j]:矩阵链 U i . . j U_{i..j} Ui..j的最优分割位置
伪代码
输入:矩阵维度数组p,矩阵的个数n
输出:最小标量乘法次数,分割方式追踪数组Rec
新建二维数组D[1..n,1..n],Rec[1..n,1..n]
//初始化
for i <- 1 to n do
| D[i,i] <- 0
end
//动态规划
for l <- 2 to n do
| for i <- 1 to n-l+1 do
| | j <- i+l-1
| | for k <- i to j-1 do
| | | q <- D[i,k]+D[k+1,j]+p[i-1]*p[k]*p[j]
| | | if q<D[i,j] then
| | | | D[i,j] <- q
| | | | Rec[i,j] <- k
| | | end
| | end
| end
end
return D[1,n],Rec
时间复杂度 O ( n 3 ) O(n^3) O(n3)