想要精通算法和SQL的成长之路 - 并查集的运用
- 前言
- 一. 并查集的使用和模板
- 1.1 初始化
- 1.2 find 查找函数
- 1.3 union 合并集合
- 1.4 connected 判断相连性
- 1.5 完整代码
- 二. 运用案例 - 省份数量
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 并查集的使用和模板
先说一下并查集的相关知识点:
- 含义:并查集,用于维护一组不相交的集合,支持合并两个集合和查询某个元素所属的集合。
- 用途:解决图论、连通性问题和动态连通性等问题。
通俗一点,可以使用并查集的算法题目有哪些特征?
- 需要将
n个不同的元素划分为不相交的集合。 - 开始的时候,每个元素自行成为一个集合,然后需要根据一定的顺序进行 合并。
- 同时还需要 查询 某个元素是否属于哪个集合。
因此并查集的基本操作可以包含两个:
- 合并:将两个不相交的集合合并成一个集合。(将其中一个集合的根节点连接到另一个集合的根节点上)
- 查找:根据某个元素,寻找到它所在集合的根节点。
1.1 初始化
首先我们考虑下,并查集里面需要有哪些数据结构:
- 需要一个
parent[]数组,用来存储每个元素对应的根节点。 - 再来一个
rank[]数组,代表以每个元素作为根节点,其所在集合的大小。即代表某个集合的深度。 - 再来一个
sum字段,代表当前的集合个数。
public class UnionFind {
/**
* 表示节点i的父节点
*/
private int[] parent;
/**
* 表示以节点i为根节点的子树的深度,初始时每个节点的深度都为0
*/
private int[] rank;
private int sum;
public UnionFind(int n) {
parent = new int[n];
rank = new int[n];
// 初始时每个节点的父节点都是它自己
for (int i = 0; i < n; i++) {
parent[i] = i;
}
sum = n;
}
}
1.2 find 查找函数
特征:
- 入参:元素
x。 - 要做的事情:不断地向上递归寻找这个
x的根节点。 - 递归终止条件:找到根节点。(根节点和元素本身一致)
代码如下:
public int find(int x) {
while (x != parent[x]) {
x = parent[x];
}
return x;
}
1.3 union 合并集合
特征:
- 入参:元素
x和y。 - 要做的事情:分别找到这两个元素的根节点:
rootX和rootY。 - 如果俩元素的根节点是同一个,说明他们在一个集合当中,不需要任何操作。
- 倘若两个元素的根节点不一样,根据两个集合的深度来判断。将深度小的那个集合,合并到深度大的集合中。同时更新对应的根节点和深度大小。
除此之外,我们还可以写一个简单的函数,用来判断两个元素是否处于同一个集合当中(或者是是否相连)
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 如果两个元素的根节点一致,不需要合并
if (rootX == rootY) {
return;
}
// 如果根节点 rootX 的深度 > rootY。
if (rank[rootX] > rank[rootY]) {
// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中
rank[rootX] += rank[rootY];
// 同时改变rootY的根节点,指向rootX。
parent[rootY] = rootX;
} else {
// 反之
rank[rootY] += rank[rootX];
parent[rootX] = rootY;
}
}
1.4 connected 判断相连性
/**
* 判断两个节点是否在同一个集合中
*/
public boolean connected(int x, int y) {
return find(x) == find(y);
}
1.5 完整代码
/**
* @author Zong0915
* @date 2023/10/4 下午2:52
*/
public class UnionFind {
/**
* 表示节点i的父节点
*/
private int[] parent;
/**
* 表示以节点i为根节点的子树的深度,初始时每个节点的深度都为0
*/
private int[] rank;
private int sum;
public UnionFind(int n) {
parent = new int[n];
rank = new int[n];
// 初始时每个节点的父节点都是它自己
for (int i = 0; i < n; i++) {
parent[i] = i;
}
sum = n;
}
public int find(int x) {
while (x != parent[x]) {
x = parent[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 如果两个元素的根节点一致,不需要合并
if (rootX == rootY) {
return;
}
// 如果根节点 rootX 的深度 > rootY。
if (rank[rootX] > rank[rootY]) {
// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中
rank[rootX] += rank[rootY];
// 同时改变rootY的根节点,指向rootX。
parent[rootY] = rootX;
} else {
// 反之
rank[rootY] += rank[rootX];
parent[rootX] = rootY;
}
}
/**
* 判断两个节点是否在同一个集合中
*/
public boolean connected(int x, int y) {
return find(x) == find(y);
}
}
二. 运用案例 - 省份数量
原题链接
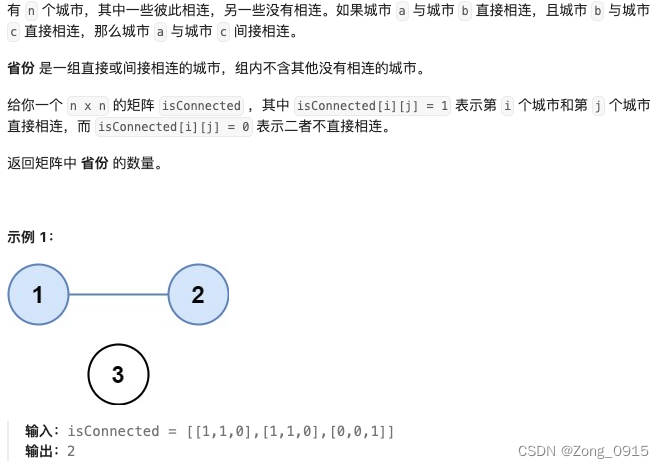
我们在并查集模板的基础上进行改造:
class UnionFind {
private int[] rank;// 每个省份具有的城市数量
private int[] parent;// 每个城市对应的根节点(省份)
private int sum;// 省份的数量
public UnionFind(int[][] isConnected) {
int len = isConnected.length;
// 初始化,省份数量和提供的城市数量一致
sum = len;
// 每个集合具有的城市数量为1
rank = new int[len];
parent = new int[len];
Arrays.fill(rank, 1);
// 根节点指向自己
for (int i = 0; i < len; i++) {
parent[i] = i;
}
}
public int find(int x) {
while (x != parent[x]) {
x = parent[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 如果两个元素的根节点一致,不需要合并
if (rootX == rootY) {
return;
}
// 如果根节点 rootX 的深度 > rootY。
if (rank[rootX] > rank[rootY]) {
// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中
rank[rootX] += rank[rootY];
// 同时改变rootY的根节点,指向rootX。
parent[rootY] = rootX;
} else {
// 反之
rank[rootY] += rank[rootX];
parent[rootX] = rootY;
}
// 合并成功,那么总集合数量要减1
sum--;
}
}
不过本题目当中,对于rank这个属性没有什么作用,最终看的是sum属性。因此大家可以把这个属性相关的给去除。
最后来看代码部分:
public int findCircleNum(int[][] isConnected) {
// 初始化构造
UnionFind unionFind = new UnionFind(isConnected);
int len1 = isConnected.length;
int len2 = isConnected[0].length;
for (int i = 0; i < len1; i++) {
for (int j = 0; j < len2; j++) {
// 如果是相连的,那么将城市 i 和 j 合并
if (isConnected[i][j] == 1) {
unionFind.union(i, j);
}
}
}
// 最后返回集合个数(即省份的个数)
return unionFind.sum;
}
最终代码如下:
public class Test547 {
public int findCircleNum(int[][] isConnected) {
UnionFind unionFind = new UnionFind(isConnected);
int len1 = isConnected.length;
int len2 = isConnected[0].length;
for (int i = 0; i < len1; i++) {
for (int j = 0; j < len2; j++) {
// 如果是相连的,那么将城市 i 和 j 合并
if (isConnected[i][j] == 1) {
unionFind.union(i, j);
}
}
}
return unionFind.sum;
}
class UnionFind {
private int[] rank;// 每个省份具有的城市数量
private int[] parent;// 每个城市对应的根节点(省份)
private int sum;// 省份的数量
public UnionFind(int[][] isConnected) {
int len = isConnected.length;
// 初始化,省份数量和提供的城市数量一致
sum = len;
// 每个集合具有的城市数量为1
rank = new int[len];
parent = new int[len];
Arrays.fill(rank, 1);
// 根节点指向自己
for (int i = 0; i < len; i++) {
parent[i] = i;
}
}
public int find(int x) {
while (x != parent[x]) {
x = parent[x];
}
return x;
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
// 如果两个元素的根节点一致,不需要合并
if (rootX == rootY) {
return;
}
// 如果根节点 rootX 的深度 > rootY。
if (rank[rootX] > rank[rootY]) {
// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中
rank[rootX] += rank[rootY];
// 同时改变rootY的根节点,指向rootX。
parent[rootY] = rootX;
} else {
// 反之
rank[rootY] += rank[rootX];
parent[rootX] = rootY;
}
sum--;
}
}
}