题目描述

作物杂交是作物栽培中重要的一步。已知有 N种作物 (编号 1 至 N )，第 i 种作物从播种到成熟的时间为 Ti。作物之间两两可以进行杂交，杂交时间取两种中时间较长的一方。如作物 A 种植时间为 5 天，作物 B 种植时间为 7 天，则 AB 杂交花费的时间为 7 天。作物杂交会产生固定的作物，新产生的作物仍然属于 N 种作物中的一种。

初始时，拥有其中 M 种作物的种子 (数量无限，可以支持多次杂交)。同时可以进行多个杂交过程。求问对于给定的目标种子，最少需要多少天能够得到。

如存在 4 种作物 ABCD，各自的成熟时间为 5 天、7 天、3 天、8 天。初始拥有 AB 两种作物的种子，目标种子为 D，已知杂交情况为 A × B → C，A × C → D。则最短的杂交过程为：

第 1 天到第 7 天 (作物 B 的时间)，A × B → C。
第 8 天到第 12 天 (作物 A 的时间)，A × C → D。
花费 12 天得到作物 D 的种子。

输入描述

输入的第 1 行包含 4 个整数 N, M, K, T 。N 表示作物种类总数 (编号 1 至 N)，M 表示初始拥有的作物种子类型数量，K 表示可以杂交的方案数，T 表示目标种子的编号。

第 2 行包含 N 个整数，其中第 i 个整数表示第 i 种作物的种植时间 Ti (1≤Ti≤100)。

第 3 行包含 M 个整数，分别表示已拥有的种子类型 Kj (1≤Kj≤M)，Kj 两两不同。

第 4 至 K + 3 行，每行包含 3 个整数 A, B,C，表示第 A 类作物和第 B 类作物杂交可以获得第 C 类作物的种子。

其中，1≤N≤2000,2≤M≤N,1≤K≤10^5,1≤T≤N, 保证目标种子一定可以通过杂交得到。

输出描述

输出一个整数，表示得到目标种子的最短杂交时间。

输入输出样例

输入

6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6

输出

样例说明

第 1 天至第 5 天，将编号 1 与编号 2 的作物杂交，得到编号 3 的作物种子。
第 6 天至第 10 天，将编号 1 与编号 3 的作物杂交，得到编号 4 的作物种子。
第 6 天至第 9 天，将编号 2 与编号 3 的作物杂交，得到编号 5 的作物种子。
第 11 天至第 16 天，将编号 4 与编号 5 的作物杂交，得到编号 6 的作物种子。
总共花费 16 天。

思路（DFS）：

题目虽然没有说明，但是测试用例之中会存在编号为C的种子有许多种合成方案。

也就是我们必须算出编号为C的种子所有方案之中耗时最短的一个方案。

我们知道，要求得到一颗种子C，所需要的耗时，就是A+B两个种子之中的最大成熟时间。

但是如果种子C，它合成方案所需要的A和B种子也都没有呢？那么就需要依次往下推，也就是需要A+B种子之中最大的成熟时间，加上合成A或者B种子所需要的最大时间。

如果这颗种子我们没有，那么我们合成这个种子所需要的时间，就是耗时。

了解了耗时之后，我们拥有的种子，那么肯定是不需要消耗时间来得到了。

如同题目给出的例子一样，我们初始拥有1和2种子，我们已经拥有了这两颗种子，那么需要得到它们的耗时就是0，那么3种子呢？

3种子我们是没有拥有的，合成他，就需要取1和2种子之中的成熟时间的最大值，也就是5，所以3种子的成熟时间是5，但是它不需要额外的耗时。

那如果我们还没有合成种子3，想合成种子4呢？那么就需要种子1和种子3，根据题目给出的成熟时间，种子4的成熟时间是max(5,4)，也就是5，但是种子3我们还没有，所以得到种子3需要耗时，这个耗时就是我们递归搜索的目的，得到每个种子最快的成熟时间+耗时。

前面我们提到过，种子3的成熟时间是5，那么种子4的成熟时间也是5，因为种子1不需要合成，所以没有额外的耗时；但是种子3没有，需要额外消耗时间去种植它，所以它的耗时是5。

这样回到种子4，那么我们得到种子4一共耗时10。

再看种子5，因为我们之前得到种子3的时候计算过，需要得到它的耗时是5，那么种子5的成熟时间是max(3,4),也就是4天，加上种子3的耗时，所以它一共需要耗时9。

说到这里大家可能有点不太理解，为什么种子5的耗时是9，而不是4呢？

我们从递归的思想出发，从种子6开始进行搜索：

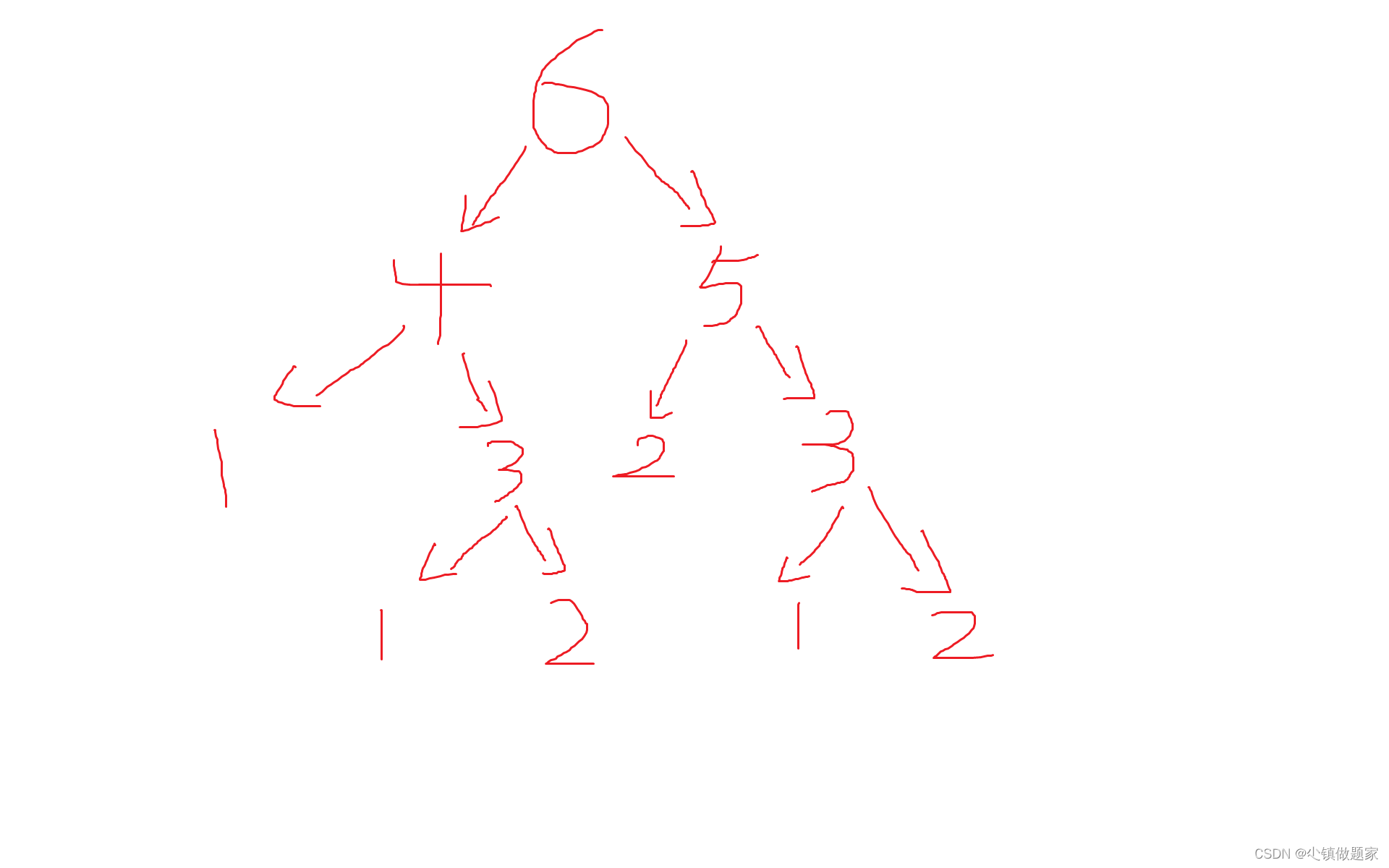
首先我们知道，6的成熟时间是4和5之间的最大值，也就是max(6,4),是6，那么我们得到4和5是不是还需要额外的耗时，去合成4和5？

那么合成4的同时也可以合成5，然后取他们之间的最大耗时，就是合成4，5一共所需要的时间。

所以这题的递归，我们只需要搜索他们该得到该种植，需要的最大成熟时间+两个种子的最大耗时。

也就是我们需要开一个数组来记录得到该种子的最大耗时，已经拥有的种子是不需要额外的耗时的，但是像种子4，它就需要额外5的耗时，加上本身成熟的时间5，一共需要的时间就是10。我们把它记录下来。

种子5也同理，它本身需要的成熟时间是4，种子3需要额外的合成时间，额外的耗时就是5，那么得到种子5的最大耗时是9.

上面我们也提到过，4和5是可以同时进行合成的，所以只需要取他们合成用的最大耗时中的最大值即可。也就是种子4和种子5之间，耗时短的是必然在耗时长的之前完成合成，但也还是需要等待耗时长的合成完毕才能继续合成种子C。所以他们之间是需要对总共耗时取一个最大值的。

所以得出种子C所需要的最短杂交时间，就为自身成熟时间+max(A耗时,B耗时);

当然，因为种子C会有不同的杂交方案，我们就需要对每一个方案进行对比，取最短的杂交时间的方案。

AC代码（Java）：

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {

    static boolean[] flag; //标记该种植是否拥有
    static int[][] line; //记录方案
    static int[] time; //该种子种植所需要的时间
    static int[] maxTime; //该种子通过杂交得到的时间
    static int[] res; //该种子最终合成需要的时间，用于dfs
    static int T;//目标种子的编号

    private static void getInputStreamData() {
        Scanner scan = new Scanner(System.in);

        //第一行的数据
        int N = scan.nextInt(); //作物种类总数
        int M = scan.nextInt(); //我们初始拥有的种子类型数量
        int K = scan.nextInt(); //可以杂交的方案数量
        int T = scan.nextInt(); //T就是目标种子的编号，我们要拿到得到这个种子的最短的杂交时间

        init(N,M,K,T);

        //第二行的数据,从1开始，通过编号找到耗时
        for(int i = 1;i<=N;i++) {
            time[i] = scan.nextInt();
        }

        //第三行数据
        for(int i = 0 ;i<M;i++) {
            int seed = scan.nextInt();
            flag[seed] = true; //标记拥有该种子
        }

        //第四行数据
        for(int i = 0;i<K;i++){
            // C = A + B
            line[i][0] = scan.nextInt(); // A
            line[i][1] = scan.nextInt(); // B
            line[i][2] = scan.nextInt(); // C
            //该种子，也就是C，得到它需要耗费的时间
        /*
          这里不用hash表记录的原因是，C可以由多种不同的方案得到，如果用hash表，hash表只会记录最新一次的方案
          所以这里通过i来记录是方案编号
        */
            maxTime[i] = Math.max( time[ line[i][0] ] ,time[ line[i][1] ] );
        }
        scan.close();
    }

    private static void init(int N,int M,int K,int t) {
        flag = new boolean[N+1]; //使得下标可以==N
        line = new int[K][3]; // line[i][0] = A,line[i][1] = B,line[i][2] = C;
        time = new int[N+1];
        maxTime = new int[K]; //maxTime记录该方案所需要的最大时间，也就是C = A+B所需要的最大时间
        res = new int[N+1]; //得到该种子的总耗时
        T = t;
    }

    public static void main(String[] args) {
        //拿数据
        getInputStreamData();
        //dfs搜索可行方案
      /*
        我们需要得到种子T，那么就要拿到种子T的最大耗时，种子T由A和B组成，那么我们拿到A和B的最大耗时
        取二者中最大一个即可。
        因为已经拥有的种子不需要耗时，也就是耗时0，所以我们可以得出递归条件就是
        当种子未拥有的时候
          maxTime[i] + Math.max( dfs( line[i][0] ) , dfs( line[i][1]) );
      */
        System.out.println( dfs(T) );
    }

    private static int dfs(int target) {

        if(flag[target] == false) { //如果该种子不存在
            int expend = Integer.MAX_VALUE;
            //遍历方案  line.length == k ,因为一个C可能有多个方案组成，我们需要通过min找到耗时最小的方案
            //所以要遍历完全部方案
            for(int i = 0;i<line.length;i++) {
                //C = A+B ,我们的target就是C
                if( line[i][2] == target) {
                    //              当前方案的最大耗时+ A和B中的最大耗时，也就是(max(A,B))
                    expend = Math.min( maxTime[i] + Math.max( dfs(line[i][0]) , dfs(line[i][1]) ) ,expend);
                }
            }
            //拿到该种子的耗时之后就可以标记我们拥有该种子了
            flag[target] = true;
            //更新得到该种子的耗时
            res[target] = expend;
        }

        return res[target];
    }
}