1、加噪过程
1、将 图像 x 0 x_0 x0 像素值映射到 [-1, 1] 之间
x 255 × 2 − 1 , w h e r e x 为图像中的像素值 \quad \frac{x}{255} \times 2-1, \quad where \; x 为图像中的像素值 255x×2−1,wherex为图像中的像素值
\quad
2、生成一张尺寸相同的噪声图片,像素值服从标准正态分布
ϵ ∼ N ( 0 , 1 ) , w h e r e ϵ 为噪声图像中的像素值 \quad \epsilon \sim N(0, 1), \quad where \; \epsilon 为噪声图像中的像素值 ϵ∼N(0,1),whereϵ为噪声图像中的像素值
\quad
3、将 处理好的原图像 和 噪音图像 进行融合
\quad 新生成的图像像素计算公式为: β × ϵ + 1 − β × x \sqrt \beta \times \epsilon + \sqrt{1-\beta} \times x β×ϵ+1−β×x , β \;\;\beta β 取值范围 为 0~1
4、 连续的对图像进行加噪

t = 1 、 2 、 3... t=1、2、3 ... t=1、2、3... 时刻的图像像素值为
x 1 = β 1 × ϵ 1 + 1 − β 1 × x 0 x 2 = β 2 × ϵ 2 + 1 − β 2 × x 1 x 3 = β 3 × ϵ 3 + 1 − β 3 × x 2 . . . . x t = β t × ϵ t + 1 − β t × x t − 1 . . . . x t = β T × ϵ T + 1 − β T × x T − 1 (1) x_1 = \sqrt \beta_1 \times \epsilon_1 + \sqrt{1-\beta_1} \times x_0 \\ x_2 = \sqrt \beta_2 \times \epsilon_2 + \sqrt{1-\beta_2} \times x_1 \\ x_3 = \sqrt \beta_3 \times \epsilon_3 + \sqrt{1-\beta_3} \times x_2 \\ .... \\ x_t = \sqrt \beta_t \times \epsilon_t + \sqrt{1-\beta_t} \times x_{t-1} \\ .... \\ x_t = \sqrt \beta_T \times \epsilon_T + \sqrt{1-\beta_T} \times x_{T-1} \tag{1} x1=β1×ϵ1+1−β1×x0x2=β2×ϵ2+1−β2×x1x3=β3×ϵ3+1−β3×x2....xt=βt×ϵt+1−βt×xt−1....xt=βT×ϵT+1−βT×xT−1(1)
备注 :
1) ϵ t \epsilon_t ϵt 都是在每个时刻 t t t 重新采样的随机数
2)每个时刻的 β t \beta_t βt 都各不相同, 0 < β t < 1 0< \beta_t <1 0<βt<1, 且 β 1 < β 2 < . . . < β T − 1 < β T \beta_1 < \beta_2 < ... < \beta_{T-1} < \beta_{T} β1<β2<...<βT−1<βT
为了简化推导过程,我们引入新的变量 α \alpha α : \quad α t = 1 − β t \alpha_t = 1-\beta_t αt=1−βt
将 α t = 1 − β t \alpha_t = 1-\beta_t αt=1−βt 带入上面的公式(1),得 :
x t = 1 − α t × ϵ t + α t × x t − 1 (2) x_t = \sqrt {1- \alpha_t} \times \epsilon_t + \sqrt{\alpha_t} \times x_{t-1} \tag{2} xt=1−αt×ϵt+αt×xt−1(2)
2、简化加噪过程
目的 : 我们想直接使用 t=0 时刻的原始图像 x 0 x_0 x0 表示 t 时刻的图像 x t x_t xt

我们一步一步来推导,我们先尝试用 x t − 2 x_{t-2} xt−2 表示 x t x_t xt
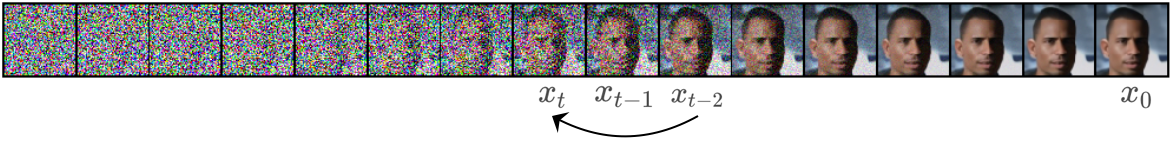
由 公式 (2), 我们可得:
x t = 1 − α t × ϵ t + α t × x t − 1 (2) x_t = \sqrt {1- \alpha_t} \times \epsilon_t + \sqrt{\alpha_t} \times x_{t-1} \tag{2} xt=1−αt×ϵt+αt×xt−1(2)
x t − 1 = 1 − α t − 1 × ϵ t − 1 + α t − 1 × x t − 2 (3) x_{t-1} = \sqrt {1- \alpha_{t-1}} \times \epsilon_{t-1} + \sqrt{\alpha_{t-1}} \times x_{t-2} \tag{3} xt−1=1−αt−1×ϵt−1+αt−1×xt−2(3)
将 公式 (3) 带入 公式 (2), 得:
x t = 1 − α t × ϵ t + α t × ( 1 − α t − 1 × ϵ t − 1 + α t − 1 × x t − 2 ) = α t ( 1 − α t − 1 ) × ϵ t − 1 + 1 − α t × ϵ t + α t α t − 1 × x t − 2 \begin{align}x_t &= \sqrt {1- \alpha_t} \times \epsilon_t + \sqrt{\alpha_t} \times (\sqrt {1- \alpha_{t-1}} \times \epsilon_{t-1} + \sqrt{\alpha_{t-1}} \times x_{t-2}) \notag \\ &= \sqrt {\alpha_t(1- \alpha_{t-1})} \times \epsilon_{t-1} + \sqrt{1-\alpha_t} \times \epsilon_t+\sqrt {\alpha_t \alpha_{t-1}} \times x_{t-2} \tag{4} \end{align} xt=1−αt×ϵt+αt