二叉搜索树
二叉搜索树又称二叉排序树,它具有以下性质的二叉树或空树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的每颗子树也分别为二叉搜索树
二叉搜索树的插入非常简单:
- 从根节点开始比较,如果大于根节点就遍历右子树,小于根节点就遍历左子树
- 对所有的子树都进行如上操作
- 直到遍历到空节点,将待插入元素插入此空节点
public class BinarySearchTree {
public static class TreeNode {
public int key;
public TreeNode left;
public TreeNode right;
TreeNode(int key) {
this.key = key;
}
}
public TreeNode root;
/**
* 插入一个元素
*/
public boolean insert(int key) {
TreeNode tmp = new TreeNode(key);
if (this.root == null) {
this.root = tmp;
return true;
}
TreeNode privat = this.root;
TreeNode p1 = this.root;
while (p1 != null) {
privat = p1;
if (p1.key > key) {
p1 = p1.left;
}else {
p1 = p1.right;
}
}
if (privat.key > key) {
privat.left = tmp;
}else {
privat.right = tmp;
}
return true;
}
}二叉搜索树的查找:
- 从根节点开始比较,如果大于根节点就遍历右子树,小于根节点就遍历左子树
- 对所有的子树都进行如上操作
//查找key是否存在
public TreeNode search(int key) {
if (this.root == null){
return null;
}
TreeNode tmp = this.root;
while (tmp != null) {
if (tmp.key > key) {
tmp = tmp.left;
}else if (tmp.key < key) {
tmp = tmp.right;
}else {
return tmp;
}
}
return null;
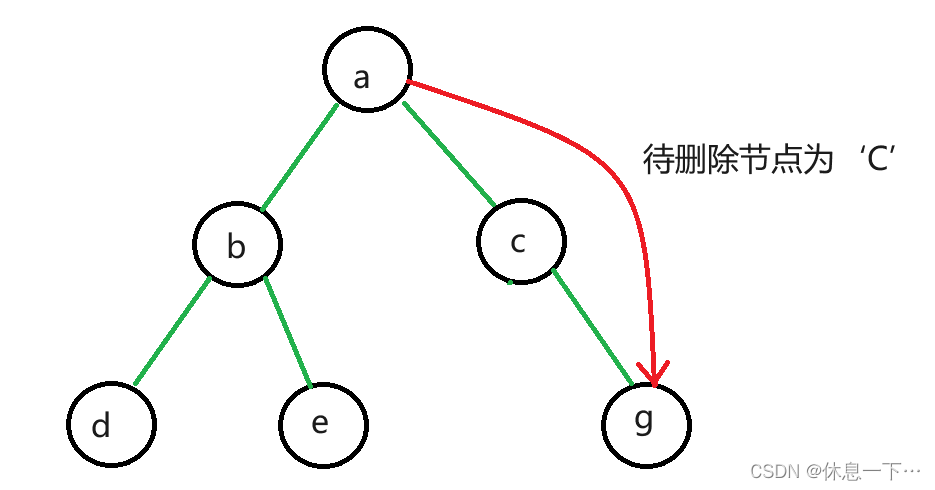
}二叉搜索树的删除比较复杂因为要保证删除之后的树依旧是一颗二叉搜索树
二叉搜索树的删除:
分两种情况:
- 左树或者右树为空
- 当待删除节点左树为空就令待删除节点的双亲指向其右子树
- 当待删除节点右树为空就令待删除节点的双亲指向其左子树
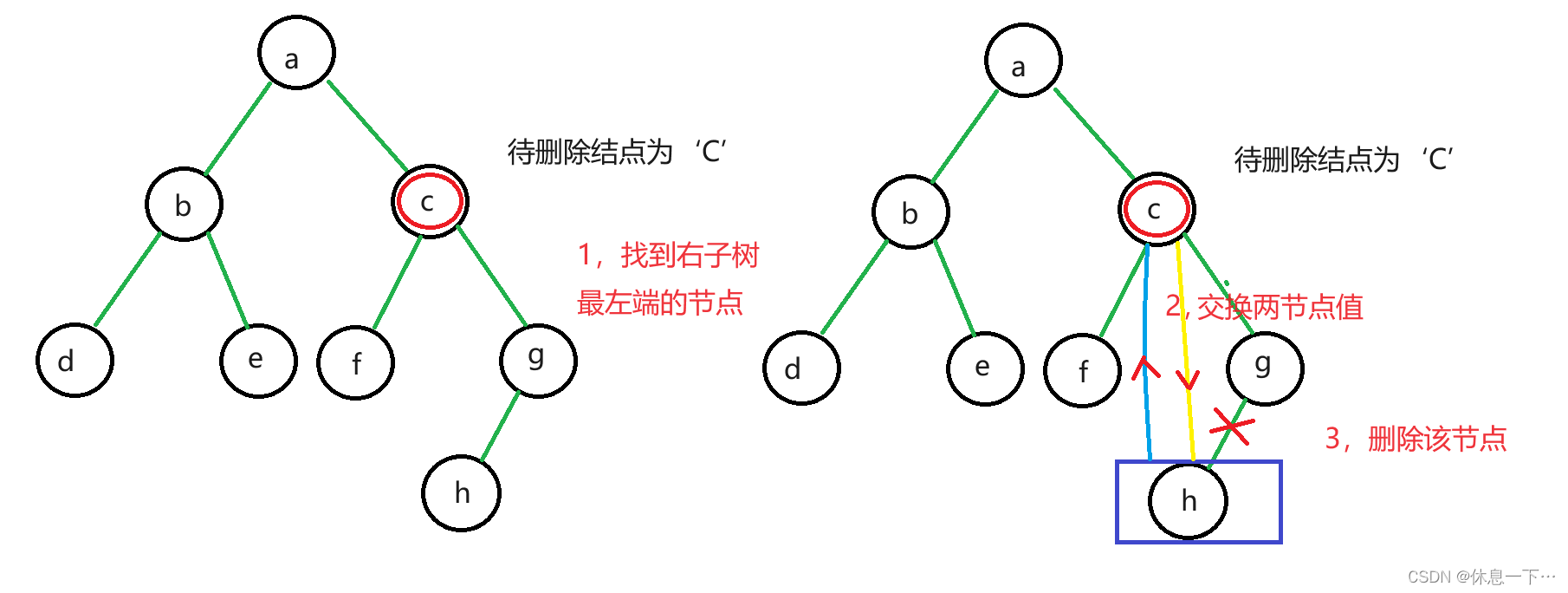
- 左右子树都不为空
- 找到右(左)子树最左(右)端的节点
- 交换两个结点的值
- 删除该节点
//删除key的值
public boolean remove(int key) {
if (this.root == null) {
return false;
}
TreeNode tmp = this.root;
TreeNode privat = tmp;
while (tmp != null) {
if (tmp.key > key) {
privat = tmp;
tmp = tmp.left;
}else if (tmp.key < key) {
privat = tmp;
tmp = tmp.right;
}else {
break;
}
}
if (tmp == null) {
return false;
}
//左树或者右树为空
if (tmp.left == null || tmp.right == null) {
if (tmp.left == null) {
if (tmp == this.root) {
this.root = tmp.right;
}else {
if (privat.left == tmp) {
privat.left = tmp.right;
}else {
privat.right = tmp.right;
}
}
}else {
if (tmp == this.root) {
this.root = tmp.left;
}else {
if (privat.left == tmp) {
privat.left = tmp.left;
}else {
privat.right = tmp.left;
}
}
}
}else {
//左右子树都不为空
TreeNode a = tmp.right;
while(a.left != null) {
privat = a;
a = a.left;
}
tmp.key = a.key;
if (privat.left == a) {
privat.left = a.right;
}else {
privat.right = a.right;
}
}
return true;
}Set 和 Map
Map和set是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。
一般把搜索的数据称为关键字(Key),和关键字对应的称为值(Value),将其称之为Key-value的键值对。
有两种模型:
- 纯 key 模型:
有一个英文词典,快速查找一个单词是否在词典中快速查找某个名字在不在通讯录中
- Key-Value 模型:
统计文件中每个单词出现的次数,统计结果是每个单词都有与其对应的次数:<单词,单词出现的次数>。

Map.Entry
Map.Entry<K, V> 是Map内部实现的用来存放<key, value>键值对映射关系的内部类
里面有这几种方法:
方法 解释 K getKey() 返回 entry 中的 key V getValue() 返回 entry 中的 value V setValue(V value) 将键值对中的value替换为指定value
Map
- Map是一个接口,不能直接实例化对象,如果要实例化对象只能实例化其实现类TreeMap或者HashMap
- Map中存放键值对的Key是唯一的,value是可以重复的
- 在TreeMap中插入键值对时,key不能为空,否则就会抛NullPointerException异常,value可以为空。但是HashMap的key和value都可以为空。
- Map中的Key可以全部分离出来,存储到Set中来进行访问(因为Key不能重复)。
- Map中的value可以全部分离出来,存储在Collection的任何一个子集合中(value可能有重复)。
- Map中键值对的Key不能直接修改,value可以修改,如果要修改key,只能先将该key删除掉,然后再来进行重新插入。
public static void main(String[] args) {
Map<Integer,Integer> map = new HashMap<>();
Map<Integer,Integer> map1 = new TreeMap<>();
}| Map底层结构 | TreeMap | HashMap |
| 底层结构 | 红黑树 | 哈希桶 |
| 插入/删除/查找时间 复杂度 | O(1) | |
| 是否有序 | 关于Key有序 | 无序 |
| 线程安全 | 不安全 | 不安全 |
| 插入/删除/查找区别 | 需要进行元素比较 | 通过哈希函数计算哈希地址 |
| 比较与覆写 | key必须能够比较,否则会抛出 ClassCastException异常 | 自定义类型需要覆写equals和 hashCode方法 |
| 应用场景 | 需要Key有序场景下 | Key是否有序不关心,需要更高的 时间性能 |
| 方法 | 解释 |
| V get(Object key) | 返回 key 对应的 value |
| V getOrDefault(Object key, V defaultValue) | 返回 key 对应的 value,key 不存在,返回默认值 |
| V put(K key, V value) | 设置 key 对应的 value |
| V remove(Object key) | 删除 key 对应的映射关系 |
| Set<K> keySet() | 返回所有 key 的不重复集合 |
| Collection<V> values() | 返回所有 value 的可重复集合 |
| Set<Map.Entry<K, V>> entrySet() | 返回所有的 key-value 映射关系 |
| boolean containsKey(Object key) | 判断是否包含 key |
| boolean containsValue(Object value) | 判断是否包含 value |
Set
- Set是继承自Collection的一个接口类
- Set中只存储了key,并且要求key一定要唯一
- TreeSet的底层是使用Map来实现的,其使用key与Object的一个默认对象作为键值对插入到Map中的
- Set最大的功能就是对集合中的元素进行去重
- 实现Set接口的常用类有TreeSet和HashSet,还有一个LinkedHashSet,LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。
- Set中的Key不能修改,如果要修改,先将原来的删除掉,然后再重新插入
- TreeSet中不能插入null的key,HashSet可以。
| Set底层结构 | TreeSet | HashSet |
| 底层结构 | 红黑树 | 哈希桶 |
| 插入/删除/查找时间 复杂度 | O(1) | |
| 是否有序 | Key有序 | 不一定有序 |
| 线程安全 | 不安全 | 不安全 |
| 插入/删除/查找区别 | 按照红黑树的特性来进行插入和删除 | 1. 先计算key哈希地址 2. 然后进行插入和删除 |
| 比较与覆写 | key必须能够比较,否则会抛出 ClassCastException异常 | 自定义类型需要覆写equals和 hashCode方法 |
| 应用场景 | 需要Key有序场景下 | Key是否有序不关心,需要更高的 时间性能 |