文章目录
- 1.边缘检测算子分类
- 2.Canny算子核心理论
- 2.1.Canny算子简单介绍
- 2.2.Canny算子边缘检测指标
- 2.3.Canny算子基本原理
- 3.Canny算子处理流程
- 3.1.高斯滤波去噪声化
- 3.2.图像梯度搜寻
- 3.3.非极大值抑制处理
- 3.4.双阈值边界处理
- 3.5.边界滞后技术跟踪
- 3.6.Canny算子边缘检测的特点
- 4.Canny算子算法代码
- 5.Canny算子效果展示
- 6.参考文章及致谢
1.边缘检测算子分类
(1)一阶导数的边缘检测算子:
通过模板作为核与图像的每个像素点做卷积和运算,然后选取合适的阈值来提取图像的边缘。常见的有Roberts算子、Sobel算子和Prewitt算子。
(2)二阶导数的边缘算子:
依据于二阶导数过零点,常见的有Laplacian 算子,此类算子对噪声敏感。
(3)Canny算子:
前面两类均是通过微分算子来检测图像边缘,还有一种就是Canny算子,其是在满足一定约束条件下推导出来的边缘检测最优化算子。
2.Canny算子核心理论
2.1.Canny算子简单介绍
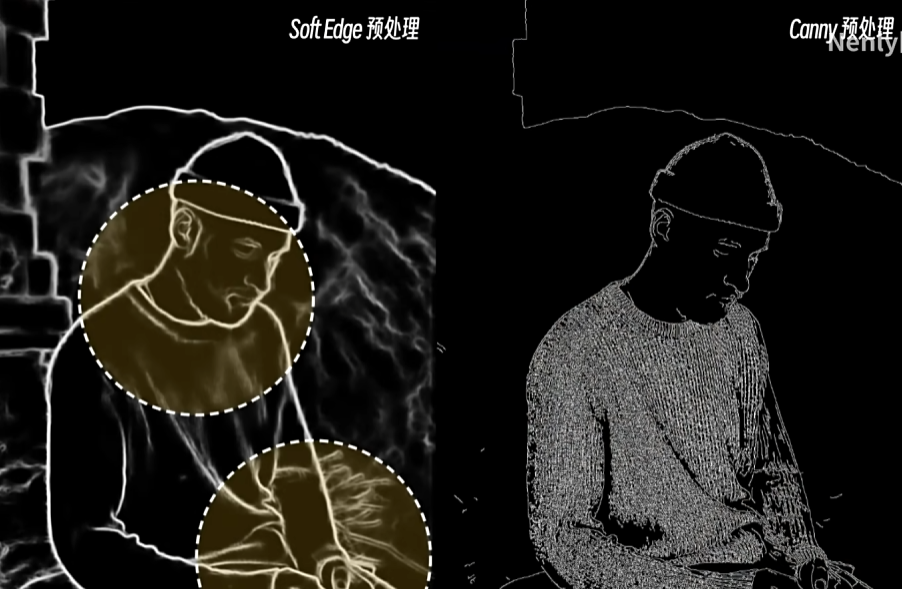
Canny算子是一种非常常用的边缘检测算子,其效果图如下所示:
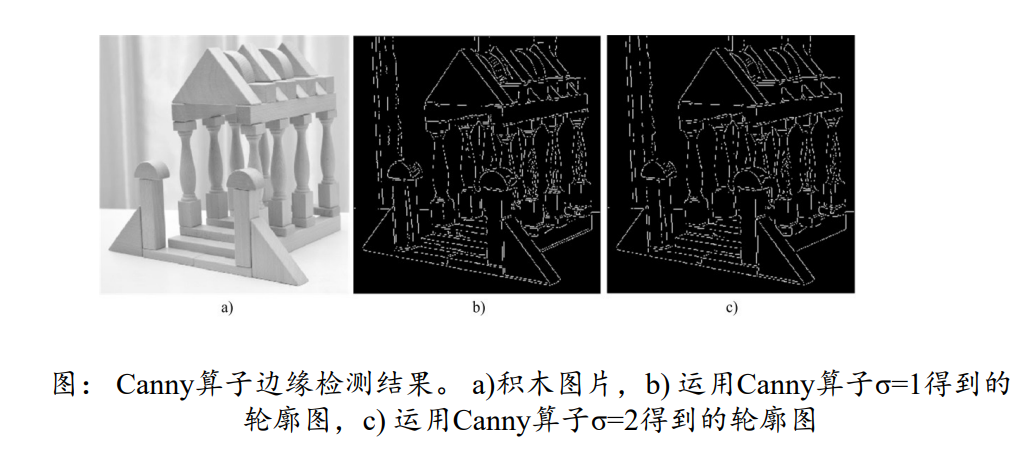
2.2.Canny算子边缘检测指标
Canny算子是基于边缘检测来实现的,那么边缘检测的指标如下所示:
(1)好的信噪比,即将非边缘点判定为边缘点的概率要低。
(2)高定位,检测出的边缘要在实际边缘中心。
(3)对单一边缘仅有唯一响应,即虚假边缘要能得到最大抑制。
2.3.Canny算子基本原理
1.2个条件:一能有效抑制噪声,二能精确定位边缘位置
2.平滑后求导,用高斯滤波器进行平滑
3.用一阶偏导有限差分计算梯度幅值与方向
3.对梯度幅值进行非极大值抑制
4.用双闯值检测与连接边缘
3.Canny算子处理流程
第三部分的内容引用自:https://blog.csdn.net/zaishuiyifangxym/article/details/90142702
我的工作就是通过其的blog来进行学习,这位博主的cv的专栏写的非常好。
如果大家这这篇blog中有什么不明白的可以去他的专栏里面看看,内容非常全面,应该能够有比较好的解答。
3.1.高斯滤波去噪声化
根据上述算法的第一个原理,我们需要对于图片影响进行去噪声化处理。
边缘检测容易受到噪声的影像。因此,在进行边缘检测前,通常需要进行去噪。通常,使用高斯滤波来去除噪声,高斯滤波去噪是比较常用的去噪函数合,其5x5的模板公式对应如下:
1
273
×
[
1
4
7
4
1
4
16
26
16
4
7
26
41
26
7
4
16
26
16
4
1
4
7
4
1
]
\frac{1}{273}\times\begin{bmatrix}1&4&7&4&1\\4&16&26&16&4\\7&26&41&26&7\\4&16&26&16&4\\1&4&7&4&1\end{bmatrix}
2731×
1474141626164726412674162616414741
在Opencv库当中,高斯滤波的函数如下所示:
img = cv2.GaussianBlur(src, ksize, sigmaX)
其中,参数:src 表示原始图像;ksize 表示核大小,而且ksize只能是奇数;sigmaX 表示X方向方差。
3.2.图像梯度搜寻
在这一部分的内容当中,我们需要去计算和找寻梯度幅值和方向,寻找图像的梯度。我们需要先将卷积模板分别作用x和y方向,再计算梯度幅值和方向,其公式如下所示:
卷积化
:
d
x
=
[
−
1
0
1
−
2
0
2
−
1
0
1
]
d
y
=
[
−
1
−
2
−
1
0
0
0
1
2
1
]
幅度
:
S
=
d
x
2
+
d
y
2
方向
:
θ
=
arctan
(
d
y
d
x
)
\begin{aligned}卷积化:d_x&=\begin{bmatrix}-1&0&1\\-2&0&2\\-1&0&1\end{bmatrix}\quad d_y=\begin{bmatrix}-1&-2&-1\\0&0&0\\1&2&1\end{bmatrix}\\\\幅度:S&=\sqrt{d_x^2+d_y^2}\\\\ 方向:\theta&=\arctan(\frac{d_y}{d_x})\end{aligned}
卷积化:dx幅度:S方向:θ=
−1−2−1000121
dy=
−101−202−101
=dx2+dy2=arctan(dxdy)
计算之后得到的幅度和方向如图所示:
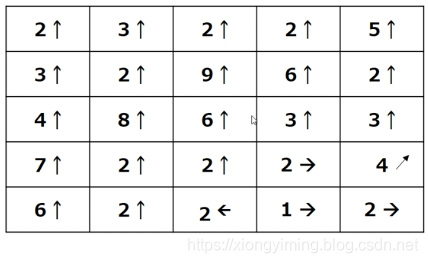
3.3.非极大值抑制处理
对于每个像素点,它进行如下操作:应用非最大抑制技术来过滤掉非边缘像素,将模糊的边界变得清晰。该过程保留了每个像素点上梯度强度的极大值,过滤掉其他的值。
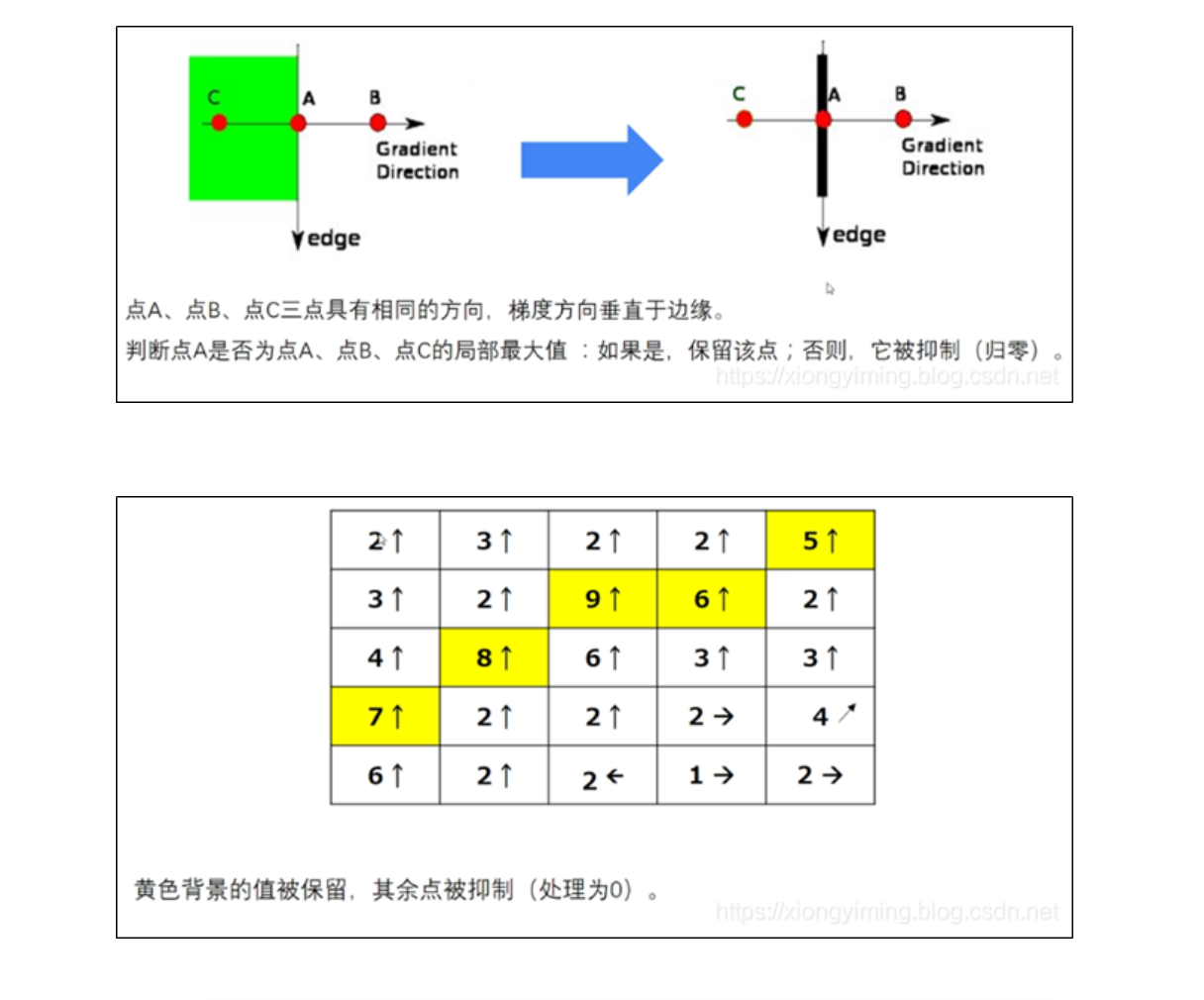
Step1:将其梯度方向近似为以下值中的一个,包括0、45、90、135、180、225、270和315,即表示上下左右和45度方向。
Step2:比较该像素点和其梯度正负方向的像素点的梯度强度,如果该像素点梯度强度最大则保留,否则抑制(删除,即置为0)。
Step1和Step2的处理方式如图所示:
3.4.双阈值边界处理
双阈值边界处理的原理也比较简单,我们对非极大值抑制图像作用两个阈值
T
l
o
w
T_{low}
Tlow和
T
h
i
g
h
T_{high}
Thigh。 把梯度值小于
T
l
o
w
T_{low}
Tlow的像素的灰度值设为0,得到图像1。然后把梯度值大于
T
h
i
g
h
T_{high}
Thigh的像素的灰度值设为0,得到图像2。
由于图像2的阈值值较高,去除大部分噪音,但同时也损失了有用的边缘信息。而图像1的阈值较低,保留了较多的信息,我们可以以图像2为基础,以图像1为补充来连结图像的边缘。
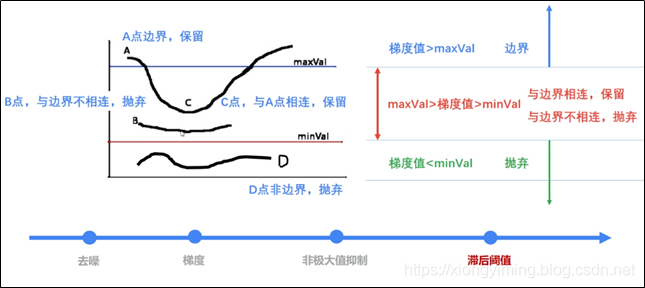
3.5.边界滞后技术跟踪
边界滞后技术跟踪的方法研究来自:https://blog.csdn.net/qq_44736333/article/details/109152380
我们假设两类边缘:经过非极大值抑制之后的边缘点中,梯度值超过T1的称为强边缘,梯度值小于T1大于T2的称为弱边缘,梯度小于T2的不是边缘。
可以肯定的是,强边缘必然是边缘点,因此必须将T1设置的足够高,以要求像素点的梯度值足够大(变化足够剧烈),而弱边缘可能是边缘,也可能是噪声,如何判断呢?
当弱边缘的周围8邻域有强边缘点存在时,就将该弱边缘点变成强边缘点,以此来实现对强边缘的补充。
实际中人们发现T1:T2=2:1的比例效果比较好,其中T1可以人为指定,也可以设计算法来自适应的指定,比如定义梯度直方图的前30%的分界线为T1,我实现的是人为指定阈值。

在上图中,白色方块代表存在边缘(包括强弱边缘),遍历弱边缘中的每个像素,如果像素的八邻域存在强边缘对应的像素,则将这个弱边缘像素归为真正的边缘(从视觉上来理解,就是存在一条不确定的边缘,如果这条不确定的边缘旁存在真正的边缘,则将这条边归为真边,非则就将其删除)
3.6.Canny算子边缘检测的特点
1.检出准则: 该准则要求不应丢失重要的边缘,而且不应输出噪声性的多余边缘。
2.定位准则: 该准则要求检测到的边缘位置与实际边缘位置之间的距离为最小。
3.单一响应准则: 该准则在一定程度上多涵盖为检出准则,它要求尽可能减少对于同一边缘出现多个响应的情况。
4.Canny算子算法代码
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def All_Canny(img):
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)#图像灰度化处理
gaussian = cv2.GaussianBlur(grayImage, (5, 5), 0)# 高斯滤波降噪
Canny = cv2.Canny(gaussian, 50, 150)# Canny算子
return grayImage, gaussian,Canny
# 读取图像
img = cv2.imread('lena.jpg')#imread出来的是BRG图像
lenna_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)#转化为RGB图像
# 显示图形
Figure=All_Canny(img)#获取Canny检测之后的图片
#图像可视化处理
titles = [u'原始图像', u'灰度处理图',u'高斯去噪处理图', u'Canny算子c处理图']
images = [lenna_img ,Figure[0],Figure[1], Figure[2]]
#subplot绘制
#第一张图
plt.subplot(2, 2, 1)
plt.imshow(images[0], 'gray'),plt.title(titles[0])
plt.xticks([]),plt.yticks([])
#第二张图
plt.subplot(2, 2, 2)
plt.imshow(images[1], 'gray'),plt.title(titles[1])
plt.xticks([]),plt.yticks([])
#第三张图
plt.subplot(2, 2, 3)
plt.imshow(images[2], 'gray'),plt.title(titles[2])
plt.xticks([]),plt.yticks([])
#第四张图
plt.subplot(2, 2, 4)
plt.imshow(images[3], 'gray'),plt.title(titles[3])
plt.xticks([]),plt.yticks([])
plt.savefig(r"D:\HuaweiMoveData\Users\27182\Desktop\py\Canny.png",dpi=1000)
plt.show()
5.Canny算子效果展示

6.参考文章及致谢
本章内容的完成离不开以下大佬文章的启发和帮助,在这里列出名单,如果对于内容还有不懂的,可以移步对应的文章进行进一步的理解分析。
1.Canny边缘检测算子流程:https://blog.csdn.net/zaishuiyifangxym/article/details/90142702
2.边界滞后技术跟踪算法:https://blog.csdn.net/qq_44736333/article/details/109152380
我的工作就是根据两位大佬的blog来进行学习,这两位博主的cv的专栏写的非常好。
如果大家这这篇blog中有什么不明白的可以去他们俩个的专栏里面看看,内容非常全面,应该能够有比较好的解答。
在文章的最后再次表达由衷的感谢!!



![[架构之路-225]:计算机硬件与体系结构 - 分类方法大汇总: RISC, CISC](https://img-blog.csdnimg.cn/00bf032590184d90aa72c9abf47b592b.png)