预备基础知识

1、概率 - 条件独立

A 和 B 是两个独立事件 $\Rightarrow P(A|B)=P(A)$，$P(B|A)=P(B)$

$\Rightarrow P(A,B|C)=P(A|C)P(B|C)$

---

2、贝叶斯公式、先验概率、后验概率、似然、证据

   \;
$叶贝斯公式：P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

• 先验概率 (prior)：P(A)
• 后验概率 (posterior) ：P(A|B)
• 似然 (likelihood)：P(B|A)
• 证据 (evidence)：{P(B)

---

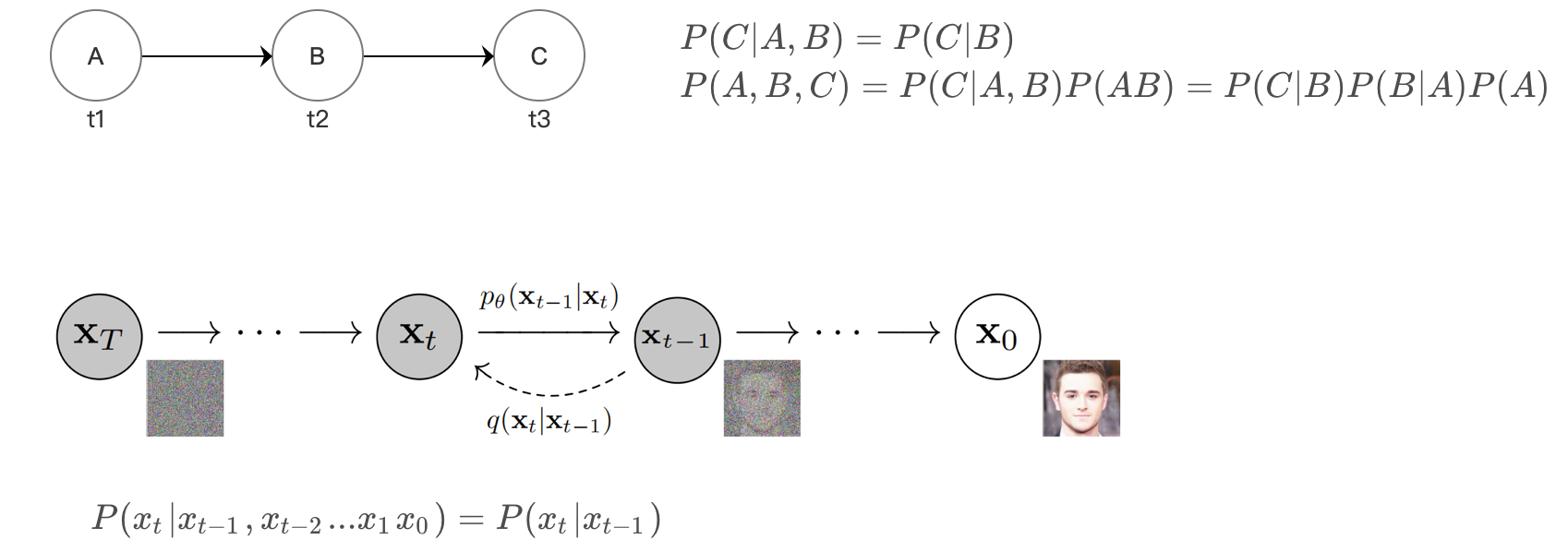
3、马尔可夫链

   \;
下一状态的概率分布仅取决于当前状态，与过去的状态无关

---

4、正态分布 / 高斯分布

   \;
$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$

高斯分布的 2个性质:

\quad \quad (1) 如果 $X\sim \mathcal{N}(\mu ,{\sigma }^2)$， 那么 $aX+b\sim \mathcal{N}(a\mu +b,a^2{\sigma }^2)$

\quad \quad (2) 两个正态分布相加，其结果也是正态分布 :

\quad \quad \quad $X\sim \mathcal{N}({\mu }_1,{\sigma }_1^2);Y\sim \mathcal{N}({\mu }_2,{\sigma }_2^2)，则X+Y\sim \mathcal{N}({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$

---

5、重参数化技巧

在含有随机变量的模型中，通常会有采样这一个步骤，而采样这个操作是不可导的，没法求出梯度，也就无法通过反向传播来对参数进行优化。

这时，我们就可以通过重参数化技巧，将 简单分布的采样结果 变换到 特定分布中，如此一来则可以对参数进行求导

将原来的采样过程，分解为2步 ：
（1）引入 服从标准正态分布的随机变量 ： $z\sim \mathcal{N}(0，1)$
（2）令 $x=\mu +\sigma z$， 这样 就满足 $X\sim \mathcal{N}(\mu ,{\sigma }^2)$

这样参数 $\mu 、\sigma$ 就可以求导了：$\frac{\partial x}{\partial \mu }=1$ , $\frac{\partial x}{\partial \sigma }=z$

---

6、期望

期望 是指随机变量取值的平均值，用来刻画随机变量的集中位置

（1）离散型 随机变量

\quad \quad 离散型随机变量X 的取值为 $x_{}$