前言

想要精通算法和SQL的成长之路 - 系列导航

一. 恢复二叉搜索树

原题链接

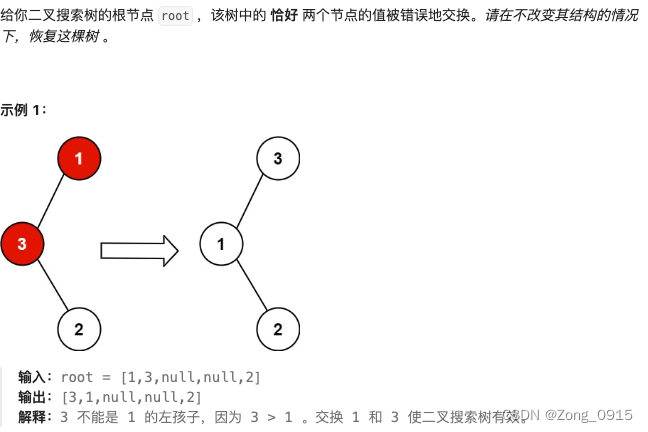
首先，一个正常地二叉搜索树在中序遍历下，遍历的元素一定是单调递增的。而题目中提醒道，正好有两个节点被互换了。那么以下面的递增序列为例：

• [1,2,3,4,5,6,7]。
• 被替换后：[1,2,6,4,5,3,7]，它一定满足一个特性：存在两个地方，满足递减的情况。
• 第一个问题点：6,4。这里我们需要找到第一个：下一个元素比当前元素小的，我们取当前元素。取前者。
• 第二个问题点：5,3，在找到第一个问题点的前提下，再找：下一个元素比当前元素小的，我们取后者。
• 最后两个问题节点值互换即可（不可以节点互换，一定是值互换）

TreeNode firstNode, secondNode, preNode = new TreeNode(Integer.MIN_VALUE);

public void recoverTree(TreeNode root) {
    inOrderReadTree(root);
    int tmp = firstNode.val;
    firstNode.val = secondNode.val;
    secondNode.val = tmp;
}

public void inOrderReadTree(TreeNode root) {
    if (root == null) {
        return;
    }
    // 左中右的顺序遍历
    inOrderReadTree(root.left);
    // 找到第一个开始递减的元素
    if (firstNode == null && preNode.val > root.val) {
        firstNode = preNode;// 取前者
    }
    // 找到第一个节点的前提下，找到第二个开始递减的元素
    if (firstNode != null && preNode.val > root.val) {
        secondNode = root;// 取后者
    }
    preNode = root;
    inOrderReadTree(root.right);
}

二. 有序链表转换二叉搜索树

原题链接

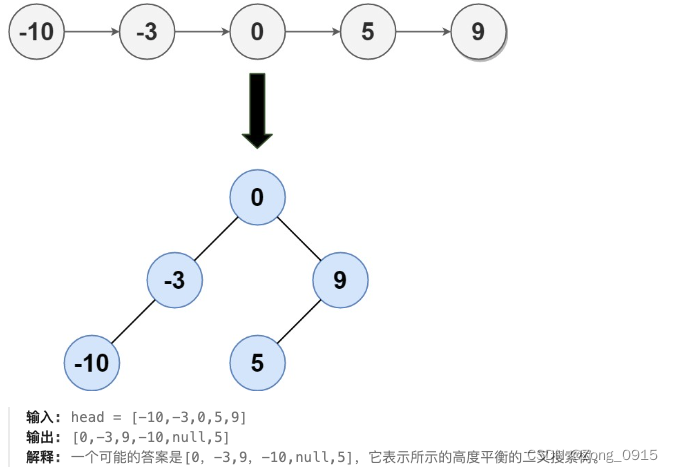
首先一点，题目的入参是一个链表，对于链表而言，不好操作，我们可以先把他转为数组：

// 构建成数组，入参是head
ArrayList<Integer> tmp = new ArrayList<>();
while (head != null) {
    tmp.add(head.val);
    head = head.next;
}
int[] arr = new int[tmp.size()];
for (int i = 0; i < arr.length; i++) {
    arr[i]= tmp.get(i);
}

其次，既然要高度平衡，那么这个题目而言，我们必定是针对转化后的数组，不断地以中间节点为根节点，向左右两侧构建树。

那么就是一个很简单的分治递归法：

public TreeNode buildTree(int left, int right, int[] arr) {
    if (left > right) {
        return null;
    }
    // 中间节点下标
    int mid = (left + right) >> 1;
    TreeNode root = new TreeNode(arr[mid]);
    root.left = buildTree(left, mid - 1, arr);
    root.right = buildTree(mid + 1, right, arr);
    return root;
}

完整代码如下：

public TreeNode sortedListToBST(ListNode head) {
    // 构建成数组
    ArrayList<Integer> tmp = new ArrayList<>();
    while (head != null) {
        tmp.add(head.val);
        head = head.next;
    }
    int[] arr = new int[tmp.size()];
    for (int i = 0; i < arr.length; i++) {
        arr[i] = tmp.get(i);
    }
    TreeNode treeNode = buildTree(0, arr.length - 1, arr);
    return treeNode;
}

public TreeNode buildTree(int left, int right, int[] arr) {
    if (left > right) {
        return null;
    }
    // 中间节点下标
    int mid = (left + right) >> 1;
    TreeNode root = new TreeNode(arr[mid]);
    root.left = buildTree(left, mid - 1, arr);
    root.right = buildTree(mid + 1, right, arr);
    return root;
}