数据结构 - 线段树的运用

news2024/11/23 2:53:29

数据结构 - 线段树的运用

  • 前言
  • 一. 线段树的运用
    • 1.1 区间和 - 线段树节点的成员变量
    • 1.2 线段树的构建
    • 1.3 线段树的区间和查询
    • 1.4 线段树的区间和更新
    • 1.5 完整代码
  • 二. 线段树的动态扩建
    • 2.1 向下递推
    • 2.2 向上递推
    • 2.3 更新操作
    • 2.4 查询操作
    • 2.5 完整代码
  • 三. 线段树的使用案例
    • 3.1 定长线段树的区间和计算
    • 3.2 动态线段树的区间和计算

前言

想要精通算法和SQL的成长之路 - 系列导航

一. 线段树的运用

我们先来看下线段树的含义：

  1. 线段树（Segment Tree）：是一种解决 区间查询问题 的数据结构。
  2. 它将一个区间划分成多个较小的子区间，并对每个子区间计算出一些有用的信息，通常是该子区间的统计值（例如最大值、最小值、总和等）。
  3. 通过将这些子区间的信息进行合并，线段树可以高效地回答各种区间查询问题。

线段树通常用于解决以下类型的问题：

  • 区间最值查询：找到给定区间内的最大值、最小值等。
  • 区间更新：对给定区间内的元素进行更新。
  • 区间求和：计算给定区间内元素的总和。

那么线段树的构建过程，通常是一个 分治递归 的过程。线段树的时间复杂度为O(logN)。

例如我们有个数组：[1,2,3,4,5]，它的区间和用线段树表示就是：
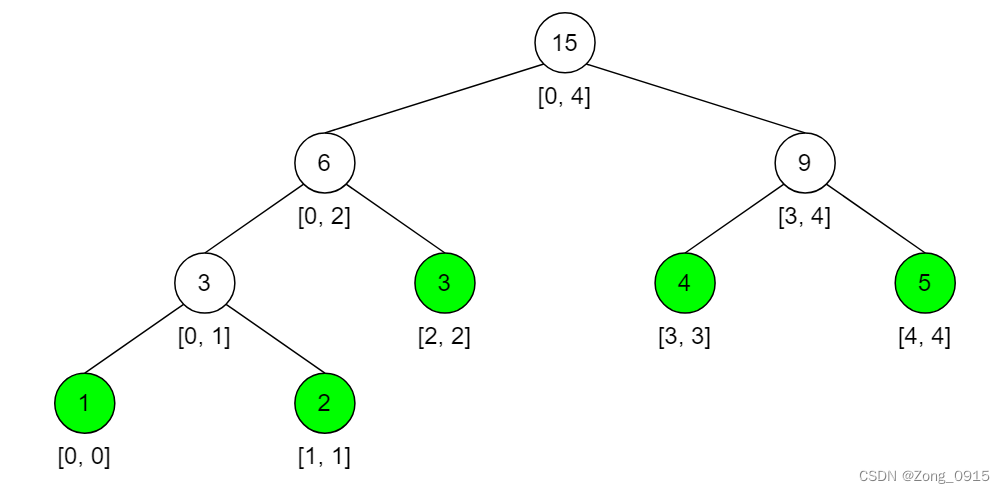
在这里插入图片描述

1.1 区间和 - 线段树节点的成员变量

首先我们思考一下，从上图中，我们一个节点需要包括哪些数据：

  • 左右节点。
  • 当前节点的左右区间。
  • 当前区间和。

那么不难得出，代码结构如下：

public class SegmentTreeNode {
    public SegmentTreeNode left;
    public SegmentTreeNode right;
    public int start;
    public int end;
    public int val;

    public SegmentTreeNode(int start, int end) {
        this.start = start;
        this.end = end;
    }
}

1.2 线段树的构建

我们往往针对的是一个数组，去构建它的线段树：

public class SegmentTree {
    // 线段树的根节点
    private SegmentTreeNode root;

    public SegmentTree(int[] nums) {
        root = buildTree(nums, 0, nums.length - 1);
    }

     private SegmentTreeNode buildTree(int[] nums, int start, int end) {
        if (start > end) {
            return null;
        }
        // 构建当前节点
        SegmentTreeNode node = new SegmentTreeNode(start, end);
        // 如果区间长度为1，那么当前节点的sum就是区间内的值
        if (start == end) {
            node.val = nums[start];
        } else {
            // 开始递归构建左右子树
            int mid = (start + end) >> 1;
            node.left = buildTree(nums, start, mid);
            node.right = buildTree(nums, mid + 1, end);
            // 当前节点的sum等于左右子树的sum之和
            node.val = node.left.val + node.right.val;
        }
        return node;
    }
}

1.3 线段树的区间和查询

构建完之后，我们需要计算区间和了：传入指定的区间queryStart和queryEnd，返回 [queryStart,queryEnd] 区间内的总和。

public int query(int queryStart, int queryEnd) {
    return queryHelper(root, queryStart, queryEnd);
}

private int queryHelper(SegmentTreeNode node, int queryStart, int queryEnd) {
    // 如果当前节点为空，或者当前节点的区间和不在查询区间内，那么返回0
    if (node == null || queryStart > node.end || queryStart < node.start) {
        return 0;
    }
    // 如果当前节点的区间完全在查询区间内，那么直接返回当前节点的sum。
    // 例如我们要查询[2,4] 的区间和，[2, 4] = [2, 2] + [3, 4]. 当前节点的区间是 [2,2] 或者 [3,4]，所以直接返回当前节点的sum即可。
    if (node.start >= queryStart && node.end <= queryEnd) {
        return node.val;
    }
    // 否则，我们需要递归查询左右子树
    int mid = (node.start + node.end) >> 1;
    // 注意这里的Math.min和Math.max，因为我们的查询区间是[queryStart, queryEnd]，而当前节点的区间是[node.start, node.end]，所以我们需要取交集
    int leftSum = queryHelper(node.left, queryStart, Math.min(queryEnd, mid));
    int rightSum = queryHelper(node.right, Math.max(queryStart, mid + 1), queryEnd);
    return leftSum
}

1.4 线段树的区间和更新

上面的区间和计算，往往是基于数组的值不变的情况下进行的。那么假若数组中的某个元素被更新了，那么我们的区间和就不正确了，跟这个元素有关的所有链路，都要被更新，因此我们还需要准备一个更新的函数，它和查询非常类似，同样是递归操作。

public void update(int index, int newVal) {
    updateHelper(root, index, newVal);
}

private void updateHelper(SegmentTreeNode node, int index, int newVal) {
    if (node == null || index < node.start || index > node.end) {
        return;
    }
    // 如果当前节点的区间就是要更新的区间，那么直接更新当前节点的sum即可
    if (node.start == node.end) {
        node.val = newVal;
        return;
    }
    // 否则，我们需要递归更新左右子树
    int mid = (node.start + node.end) >> 1;
    if (index <= mid) {
        updateHelper(node.left, index, newVal);
    } else {
        updateHelper(node.right, index, newVal);
    }
    // 更新完左右子树之后，需要更新当前节点的sum
    node.val = node.left.val + node.right.val;
}

1.5 完整代码

public class SegmentTree {
    // 线段树的根节点
    private SegmentTreeNode root;

    public SegmentTree(int[] nums) {
        root = buildTree(nums, 0, nums.length - 1);
    }

    private SegmentTreeNode buildTree(int[] nums, int start, int end) {
        if (start > end) {
            return null;
        }
        // 构建当前节点
        SegmentTreeNode node = new SegmentTreeNode(start, end);
        // 如果区间长度为1，那么当前节点的sum就是区间内的值
        if (start == end) {
            node.val = nums[start];
        } else {
            // 开始递归构建左右子树
            int mid = (start + end) >> 1;
            node.left = buildTree(nums, start, mid);
            node.right = buildTree(nums, mid + 1, end);
            // 当前节点的sum等于左右子树的sum之和
            node.val = node.left.val + node.right.val;
        }
        return node;
    }

    public int query(int queryStart, int queryEnd) {
        return queryHelper(root, queryStart, queryEnd);
    }

    private int queryHelper(SegmentTreeNode node, int queryStart, int queryEnd) {
        // 如果当前节点为空，或者当前节点的区间和不在查询区间内，那么返回0
        if (node == null || queryStart > node.end || queryStart < node.start) {
            return 0;
        }
        // 如果当前节点的区间完全在查询区间内，那么直接返回当前节点的sum。
        // 例如我们要查询[2,4] 的区间和，[2, 4] = [2, 2] + [3, 4]. 当前节点的区间是 [2,2] 或者 [3,4]，所以直接返回当前节点的sum即可。
        if (node.start >= queryStart && node.end <= queryEnd) {
            return node.val;
        }
        // 否则，我们需要递归查询左右子树
        int mid = (node.start + node.end) >> 1;
        // 注意这里的Math.min和Math.max，因为我们的查询区间是[queryStart, queryEnd]，而当前节点的区间是[node.start, node.end]，所以我们需要取交集
        int leftSum = queryHelper(node.left, queryStart, Math.min(queryEnd, mid));
        int rightSum = queryHelper(node.right, Math.max(queryStart, mid + 1), queryEnd);
        return leftSum + rightSum;
    }

    public void update(int index, int newVal) {
        updateHelper(root, index, newVal);
    }

    private void updateHelper(SegmentTreeNode node, int index, int newVal) {
        if (node == null || index < node.start || index > node.end) {
            return;
        }
        // 如果当前节点的区间就是要更新的区间，那么直接更新当前节点的sum即可
        if (node.start == node.end) {
            node.val = newVal;
            return;
        }
        // 否则，我们需要递归更新左右子树
        int mid = (node.start + node.end) >> 1;
        if (index <= mid) {
            updateHelper(node.left, index, newVal);
        } else {
            updateHelper(node.right, index, newVal);
        }
        // 更新完左右子树之后，需要更新当前节点的sum
        node.val = node.left.val + node.right.val;
    }
}

二. 线段树的动态扩建

第一节的代码，它有一个前提：

  • 我们已知数组的长度和各个元素的值。

那如果我们不知道数组包含的元素个数以及各个元素值的时候，怎么去建立这颗线段树？如果可以，它必定是在不断地更新的基础上去动态扩建的。

还是以求区间和为例，我们试想一下，在动态扩建的过程中，每个新节点需要向其他节点传递什么信息？

  • 本次应该新增的值，我们用一个变量add来标识。
  • 同时，由于数组的范围不再是固定，因此数据结构中应该剔除start和end属性。
public static class SegmentTreeNode {
    public SegmentTreeNode left;
    public SegmentTreeNode right;
    public int add;
    public int val;
    public SegmentTreeNode() {}
}

2.1 向下递推

我们定义一个pushDown函数，它的功能有这么几个：

  • 动态创建左右子节点。
  • 给左右子节点传递add值，以及计算他们的区间和val。
  • 若传递结束，那么要将当前节点的add值置为0。

考虑到add值的传递，以及树中叶子节点的性质，除了当前节点node，我们还需要两个变量来标识当前节点的左孩子数量和右孩子数量。

代码如下：

private void pushDown(SegmentTreeNode node, int leftNum, int rightNum) {
    // 动态开点
    if (node.left == null) {
        node.left = new SegmentTreeNode();
    }
    if (node.right == null) {
        node.right = new SegmentTreeNode();
    }
    // 如果当前节点的add值为0，那么我们不需要更新子节点的add值
    if (node.val == 0) {
        return;
    }
    // 否则，更新左右子节点的add值
    node.left.add += node.add * leftNum;
    node.right.add += node.add * rightNum;
    // 更新左右子节点的add值
    node.left.val += node.add;
    node.right.val += node.add;
    // 更新当前节点的add值
    node.add = 0;
}

2.2 向上递推

我们定义一个函数pushUp，主要用来计算当前节点的区间值：

  • 当前节点的区间值 = 左区间和 + 右区间和。
private void pushUp(SegmentTreeNode node) {
    node.val = node.left.val + node.right.val;
}

2.3 更新操作

/**
* @param node  线段树的根节点
 * @param start 线段树的起始位置
 * @param end   线段树的结束位置
 * @param left  查询区间的左边界
 * @param right 查询区间的右边界
 * @param addValue   比原本的值多加的值
 */
public void update(SegmentTreeNode node, int start, int end, int left, int right, int addValue) {
    // 如果线段树的区间完全在查询区间内，那么直接更新当前节点的add值即可
    if (start >= left && end <= right) {
        // 该区间内，所有叶子节点都要加上val
        node.val += (end - start + 1) * addValue;
        // 该区间内，所有非叶子节点都要加上val,传递给后面的新节点
        node.add += addValue;
        return;
    }
    // 如果不在查询区间内，那么我们需要递归更新左右子树
    int mid = (start + end) >> 1;
    // 向下传递标记
    pushDown(node, mid - start + 1, end - mid);
    if (left <= mid) {
        update(node.left, start, mid, left, right, addValue);
    }
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (right > mid) {
        update(node.right, mid + 1, end, left, right, addValue);
    }
    // 计算当前节点的val值
    pushUp(node);
}

2.4 查询操作

public int query(SegmentTreeNode node, int start, int end, int left, int right) {
    if (left <= start && end <= right) {
        return node.val;
    }
    // 把当前区间 [start, end] 均分得到左右孩子的区间范围
    int mid = (start + end) >> 1, ans = 0;
    // 下推标记
    pushDown(node, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (left <= mid) {
        ans += query(node.left, start, mid, left, right);
    }
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (right > mid) {
        ans += query(node.right, mid + 1, end, left, right);
    }
    return ans;
}

2.5 完整代码

public class SegmentTreeDynamic {
    public static class SegmentTreeNode {
        public SegmentTreeNode left;
        public SegmentTreeNode right;
        public int add;
        public int val;

        public SegmentTreeNode() {
        }
    }

    /**
     * @param node     线段树的根节点
     * @param leftNum  左节点的叶子数量
     * @param rightNum 右节点的叶子数量
     */
    private void pushDown(SegmentTreeNode node, int leftNum, int rightNum) {
        // 动态开点
        if (node.left == null) {
            node.left = new SegmentTreeNode();
        }
        if (node.right == null) {
            node.right = new SegmentTreeNode();
        }
        // 如果当前节点的add值为0，那么我们不需要更新子节点的add值
        if (node.val == 0) {
            return;
        }
        // 否则，更新左右子节点的add值
        node.left.add += node.add * leftNum;
        node.right.add += node.add * rightNum;
        // 更新左右子节点的add值
        node.left.val += node.add;
        node.right.val += node.add;
        // 更新当前节点的add值
        node.add = 0;
    }

    private void pushUp(SegmentTreeNode node) {
        node.val = node.left.val + node.right.val;
    }

    /**
     * @param node  线段树的根节点
     * @param start 线段树的起始位置
     * @param end   线段树的结束位置
     * @param left  查询区间的左边界
     * @param right 查询区间的右边界
     * @param addValue   比原本的值多加的值
     */
    public void update(SegmentTreeNode node, int start, int end, int left, int right, int addValue) {
        // 如果线段树的区间完全在查询区间内，那么直接更新当前节点的add值即可
        if (start >= left && end <= right) {
            // 该区间内，所有叶子节点都要加上val
            node.val += (end - start + 1) * addValue;
            // 该区间内，所有非叶子节点都要加上val,传递给后面的新节点
            node.add += addValue;
            return;
        }
        // 如果不在查询区间内，那么我们需要递归更新左右子树
        int mid = (start + end) >> 1;
        // 向下传递标记
        pushDown(node, mid - start + 1, end - mid);
        if (left <= mid) {
            update(node.left, start, mid, left, right, addValue);
        }
        // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
        if (right > mid) {
            update(node.right, mid + 1, end, left, right, addValue);
        }
        // 计算当前节点的val值
        pushUp(node);
    }

    public int query(SegmentTreeNode node, int start, int end, int left, int right) {
        if (left <= start && end <= right) {
            return node.val;
        }
        // 把当前区间 [start, end] 均分得到左右孩子的区间范围
        int mid = (start + end) >> 1, ans = 0;
        // 下推标记
        pushDown(node, mid - start + 1, end - mid);
        // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
        if (left <= mid) {
            ans += query(node.left, start, mid, left, right);
        }
        // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
        if (right > mid) {
            ans += query(node.right, mid + 1, end, left, right);
        }
        return ans;
    }
}

三. 线段树的使用案例

Demo如下：数组：[1, 3, 5, 7, 9, 11]。

  1. 求得区间[1,4]的区间和。
  2. 如果索引为2的地方的值更新为19，求得区间[1,4]的区间和。

3.1 定长线段树的区间和计算

public static void main(String[] args) {
    int[] nums = {1, 3, 5, 7, 9, 11};
    SegmentTree segmentTree = new SegmentTree(nums);
    int sum = segmentTree.query(1, 4); // 查询区间[1, 4]的和 3+5+7+9=24
    System.out.println(sum); // 输出：24

    segmentTree.update(2, 19); // 将索引2处的值更新为19
    sum = segmentTree.query(1, 4); // 再次查询区间[1, 4]的和
    System.out.println(sum); // 输出：38
}

结果如下：
在这里插入图片描述

3.2 动态线段树的区间和计算

public static void main(String[] args) {
    int[] nums = {1, 3, 5, 7, 9, 11};
    SegmentTreeDynamic segmentTree = new SegmentTreeDynamic();
    SegmentTreeDynamic.SegmentTreeNode root = new SegmentTreeDynamic.SegmentTreeNode();
    int n = nums.length - 1;
    for (int i = 0; i < nums.length; i++) {
        segmentTree.update(root, 0, n, i, i, nums[i]);
    }

    System.out.println(segmentTree.query(root, 0, n, 1, 4));
    segmentTree.update(root, 0, n, 2, 2, 14);// 在原本值的基础上再多14，相当于定长计算中的5 + 14 = 19
    System.out.println(segmentTree.query(root, 0, n, 1, 4));
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1057568.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

c++学习之优先级队列

c++学习之优先级队列

目录 1.初识优先级队列 库中的实现 使用优先级队列 2.优先级队列的实现 3.仿函数 利用仿函数实现的优先级队列 迭代器区间构造&#xff08;建堆&#xff09; 1.初识优先级队列 如果我们给每个元素都分配一个数字来标记其优先级&#xff0c;不妨设较小的数字具有较…
阅读更多...
2023年中国新能源汽车电动助力转向系统行业现状分析：随着新能源汽车的发展，产品渗透率的提升[图]

2023年中国新能源汽车电动助力转向系统行业现状分析：随着新能源汽车的发展，产品渗透率的提升[图]

电动助力转向(EPS)系统是传统转向系统&#xff08;如液压和电动液压系统&#xff09;的替代品。自动驾驶汽车的日益普及正在推动全球电动助力转向系统市场的需求增长。配备电动助力转向系统的车辆总重量趋于减轻&#xff0c;从而进一步提高燃油效率&#xff0c;其中2022年中国新…
阅读更多...
Nginx之Openresty基本使用解读

Nginx之Openresty基本使用解读

目录 Openresty基本介绍 Openresty源码编译安装 Openresty基本使用 测试lua脚本 外部分文件导入 关闭缓存&#xff0c;开启热部署 用lua代码获取系统变量 Openresty基本介绍 OpenResty是一个基于 Nginx 与 Lua 的高性能 Web 平台&#xff0c;其内部集成了大量精良的 Lua…
阅读更多...
2023年中国纯棉纱行业现状及发展前景分析[图]

2023年中国纯棉纱行业现状及发展前景分析[图]

棉纱是棉纤维经纺纱工艺加工而成的纱&#xff0c;经合股加工后称为棉线。根据纺纱的不同工艺&#xff0c;可分为普梳纱和精梳纱。精梳纱选用优质原料&#xff0c;成纱中纤维伸直平行、结杂少、光泽好、条干匀、强力高&#xff0c;这类棉纱多用于织造高档。 棉纱分类 资料来源&…
阅读更多...
2023年中国汽车座舱行业发展现状及趋势分析：高级人机交互（HMI）系统将逐步提升[图]

2023年中国汽车座舱行业发展现状及趋势分析：高级人机交互（HMI）系统将逐步提升[图]

2022年有22.3%的汽车用户认为座舱内车载娱乐功能成为影响使用体验的关键因素。当前智能电动汽车的用户画像与娱乐、游戏等应用的用户画像相似&#xff0c;均以年轻人作为目标用户。年轻化的用户将娱乐功能的使用习惯延伸至汽车座舱内&#xff0c;对于座舱功能的需求不再局限于导…
阅读更多...
【C语言】宏定义

【C语言】宏定义

&#x1f6a9; WRITE IN FRONT&#x1f6a9; &#x1f50e; 介绍&#xff1a;"謓泽"正在路上朝着"攻城狮"方向"前进四"&#x1f50e;&#x1f3c5; 荣誉&#xff1a;2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4、2021|2222年获评百大博…
阅读更多...
RFID藏品管理系统-智慧文物仓库管理系统

RFID藏品管理系统-智慧文物仓库管理系统

一、项目背景 RFID藏品管理系统DW-S407是一套成熟系统&#xff0c;依托互3D技术、云计算、大数据、RFID技术、智能传感器、AI、视频分析技术对文物仓库进行统一管理、分析的信息化、智能化、规范化的系统。 不管是博物馆还是艺术馆&#xff0c;藏品的管理都是非常复杂的。特…
阅读更多...
使用Docker部署ElasticSearch7+ELK（附带ES操作操作命令集）

使用Docker部署ElasticSearch7+ELK（附带ES操作操作命令集）

ElasticSearch 7ELK 程序安装Docker安装下载ES镜像提前创建挂载文件夹添加配置文件创建并启动容器可能出现的异常安装IK分词使用ElasticHD客户端工具(目前使用发现无法做增删改)安装Kibana 软件包安装安装ElasticSearch&#xff08;需要JDK1.8&#xff09;安装IK&#xff08;下…
阅读更多...
【高阶数据结构】哈希（哈希表、哈希桶）

【高阶数据结构】哈希（哈希表、哈希桶）

⭐博客主页&#xff1a;️CS semi主页 ⭐欢迎关注&#xff1a;点赞收藏留言 ⭐系列专栏&#xff1a;C进阶 ⭐代码仓库&#xff1a;C进阶 家人们更新不易&#xff0c;你们的点赞和关注对我而言十分重要&#xff0c;友友们麻烦多多点赞&#xff0b;关注&#xff0c;你们的支持是我…
阅读更多...
Codeforces Round 901 (Div. 2)

Codeforces Round 901 (Div. 2)

Problem - A - Codeforces 贪心 每次都先让b减到1&#xff0c;然后再去选择工具来增加时间 AC代码: #include<bits/stdc.h> #define endl \n #define int long long using namespace std; const int N110; int x[N]; int a,b,n; void solve() {cin>>a>>b…
阅读更多...
【C语言】模拟实现strlen

【C语言】模拟实现strlen

strlen是非常常用的字符串函数 目录 介绍&#xff1a;模拟实现&#xff1a;计数器递归指针-指针 介绍&#xff1a; 我们可得这个函数是求在字符串开始与\0之间的字符串长度 代码示例&#xff1a; #include <stdio.h> int main() {const char* str1 "abcdef"…
阅读更多...
神器 CodeWhisperer

神器 CodeWhisperer

这两天看到了好多关于 Amazon CodeWhisperer 针对个人用户终身免费使用的消息&#xff0c;便抽空简单来重点介绍下如何在 VS Code 这款 IDE 上安装和使用 CodeWhisperer。 亚马逊云科技开发者社区为开发者们提供全球的开发技术资源。这里有技术文档、开发案例、技术专栏、培训视…
阅读更多...
Linux——进程间通信——system V系列

Linux——进程间通信——system V系列

✅<1>主页&#xff1a;&#xff1a;我的代码爱吃辣 &#x1f4c3;<2>知识讲解&#xff1a;Linux——进程间通信——system V系列 ☂️<3>开发环境&#xff1a;Centos7 &#x1f4ac;<4>前言&#xff1a;system V 版本进程间通信的机制。 目录 一.共享…
阅读更多...
WebGPU 入门：绘制一个三角形

WebGPU 入门：绘制一个三角形

大家好&#xff0c;我是前端西瓜哥。 今天我们来入门 WebGPU&#xff0c;来写一个图形版本的 Hello World&#xff0c;即绘制一个三角形。 WebGPU 是什么&#xff1f; WebGPU 是一个正在开发中的潜在 Web 标准和 JavaScript API&#xff0c;目标是提供 “现代化的 3D 图形和计…
阅读更多...
AutoCAD 产品设计：图形单位

AutoCAD 产品设计：图形单位

本文讲解 AutoCAD 产品的图形单位功能产品设计&#xff0c;没有任何代码实现。 使用的 AutoCAD 为 2020 版本 图形单位是什么&#xff1f; 图形单位是用于设置 一些属性数据应该用什么格式显示 的命令&#xff0c;命令标识为 un&#xff08;units&#xff09;。 举个例子。 …
阅读更多...
操作EXCEL计算3万条数据的NDVI并填入

操作EXCEL计算3万条数据的NDVI并填入

Python操作EXCEL&#xff0c;计算3万条数据的NDVI并填入 问题描述 现在是有构建好了的查找表&#xff0c;不过构建了3万条数据&#xff0c;在excel中手动计算每行的NDVI值太麻烦了&#xff0c;也不会操作。 就试试python吧&#xff0c;毕竟python自动处理大型EXCEL数据很方便…
阅读更多...
黑马头条项目环境搭建

黑马头条项目环境搭建

注册中心网关配置 spring:cloud:gateway:globalcors:add-to-simple-url-handler-mapping: truecorsConfigurations:[/**]:allowedHeaders: "*"allowedOrigins: "*"allowedMethods:- GET- POST- DELETE- PUT- OPTIONroutes:# 平台管理- id: useruri: lb://…
阅读更多...
51单片机可调幅度频率波形信号发生器( proteus仿真+程序+原理图+报告+讲解视频）

51单片机可调幅度频率波形信号发生器( proteus仿真+程序+原理图+报告+讲解视频）

51单片机可调幅度频率信号发生器( proteus仿真程序原理图报告讲解视频&#xff09; 讲解视频1.主要功能&#xff1a;2.仿真3. 程序代码4. 原理图4. 设计报告5. 设计资料内容清单&&下载链接***[资料下载链接](https://docs.qq.com/doc/DS1daV1BKRXZMeE9u)*** 51单片机可…
阅读更多...
数据结构——计数与归并非递归

数据结构——计数与归并非递归

排序算法 前言一、归并的非递归实现二、计数排序三、序算法复杂度及稳定性分析总结 前言 重要的事说三遍&#xff01; 学习&#xff01;学习&#xff01;学习&#xff01; 努力!努力!努力&#xff01; 一、归并的非递归实现 代码实现&#xff1a; void MergeSortNonR(int* a,…
阅读更多...
3分钟在移动盘上安装Ubuntu系统和ROS2

3分钟在移动盘上安装Ubuntu系统和ROS2

目录 原视频准备烧录 一个usb移动固态硬盘可以干什么呢&#xff1f; 可以用移动盘解决电脑存储空间不足的问题&#xff0c;可以用移动盘存储数据&#xff0c;可以用移动盘装其他系统当做双系统来使用&#xff0c;可以在一个移动固态硬盘里装两个甚至更多的系统… 下面&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023