1. 引言

前序博客：

• ECDSA VS Schnorr signature VS BLS signature

ECDSA，全称为Elliptic curve Digital Signature Algorithm，采用Elliptic curve cryptography来实现的数字签名算法。

公私钥对$(pk,P)$，其中公钥$P=pk\times G$，$G$为所选椭圆曲线的base point。（elliptic curve base point: a point on the curve that generates a subgroup of large prime order $n$。 $n\times G=\mathcal{O}$, $\mathcal{O}$ is the identity element。）

1.1 ECDSA签名

ECDSA对消息$m$的签名流程为：

• 1）计算消息$m$的hash值：$e=hash(m)$。（hash函数可为SHA-2，输出转换为数值。）
• 2）若group order $n$的bit length为$L_n$，则取$e$值最左侧的$L_n$ bits赋值给$z$。（注意，$z$值可以比$n$大，但bit length不能比$n$的长。）
• 3）选择随机数$k{\in }_R[1,n-1]$。（注意，不信任一般的随机数生成器，因为不好的RNG有太多的failures和vulnerabilities，可采用RFC6979 根据$pk$和$m$来计算deterministic $k$。）（如：2013年8月，安卓Bit0coin钱包因使用了错误的随机数生成器，引起私钥泄露，导致资金损失；2010年12月，索尼PS3游戏机因错误的使用了静态而不是随机的$k$值，导致其ECDSA私钥泄露。）
• 4）计算curve point $(x_1,y_1)=k\times G$。
• 5）计算$r=x_1\mathrm{mod}n$，若$r=0$，则跳转继续执行步骤3）。
• 6）计算$s=(z+r\cdot pk)/k\mathrm{mod}n$，若$s=0$，则跳转继续执行步骤3）。
• 7）最终的签名为$(r,s)$。（注意，$(r,-s\mathrm{mod}n)$也为有效签名。）
  【根据 BIP-62 以及EIP-2可知，为了解决ECDSA签名的malleability问题，可对签名中的$s$值进行约束，限定$s$值不高于曲线order的一半。】

整个ECDSA签名流程中，要求：

• $k$值应为secret。
• 不同的签名应选择不同的$k$值，否则会泄露私钥$pk$。
  

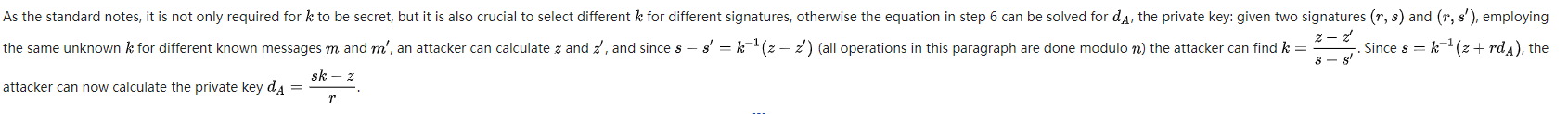
1.2 ECDSA验签

对收到的签名$(r,s)$，采用公钥$P$进行验签的流程为：

• 1）验证公钥$P$不等于identity element $\mathcal{O}$，且为其坐标为valid。
• 2）验证公钥$P$ lies on the curve。
• 3）验证公钥$P$的order为$n$，即$n\times P=\mathcal{O}$。
• 4）验证签名$(r,s)$有效，即满足$r\in [1,n-1],s\in [1,n-1]$。
• 5）计算消息$m$的hash值，所采用的hash函数应与签名时一致。$e=hash(m)$。
• 6）取$e$的最左侧$L_n$ bits赋值给$z$。
• 7）计算$u_1=z/s\mathrm{mod}n,u_2=r/s\mathrm{mod}n$。
• 8）计算curve point $(x_1,y_1)=u_1\times G+u_2\times P$。若$(x_1,y_1)=\mathcal{O}$，则签名无效。
• 9）若$r\equiv x_1(\mathrm{mod}n)$成立，则签名有效，否则签名无效。

注意，以上ECDSA验签算法可做如下改进：

• 只计算一次$1/s\mathrm{mod}n$。
• 使用Shamir’s trick，a sum of two scalar multiplication $u_1\times G+u_2\times P$ can be calculated faster than two scalar multiplications done independently。（参考2014年论文《The Double-Base Number System in Elliptic Curve Cryptograhy》）

ECDSA总的签名和验签流程可以如下图示意：

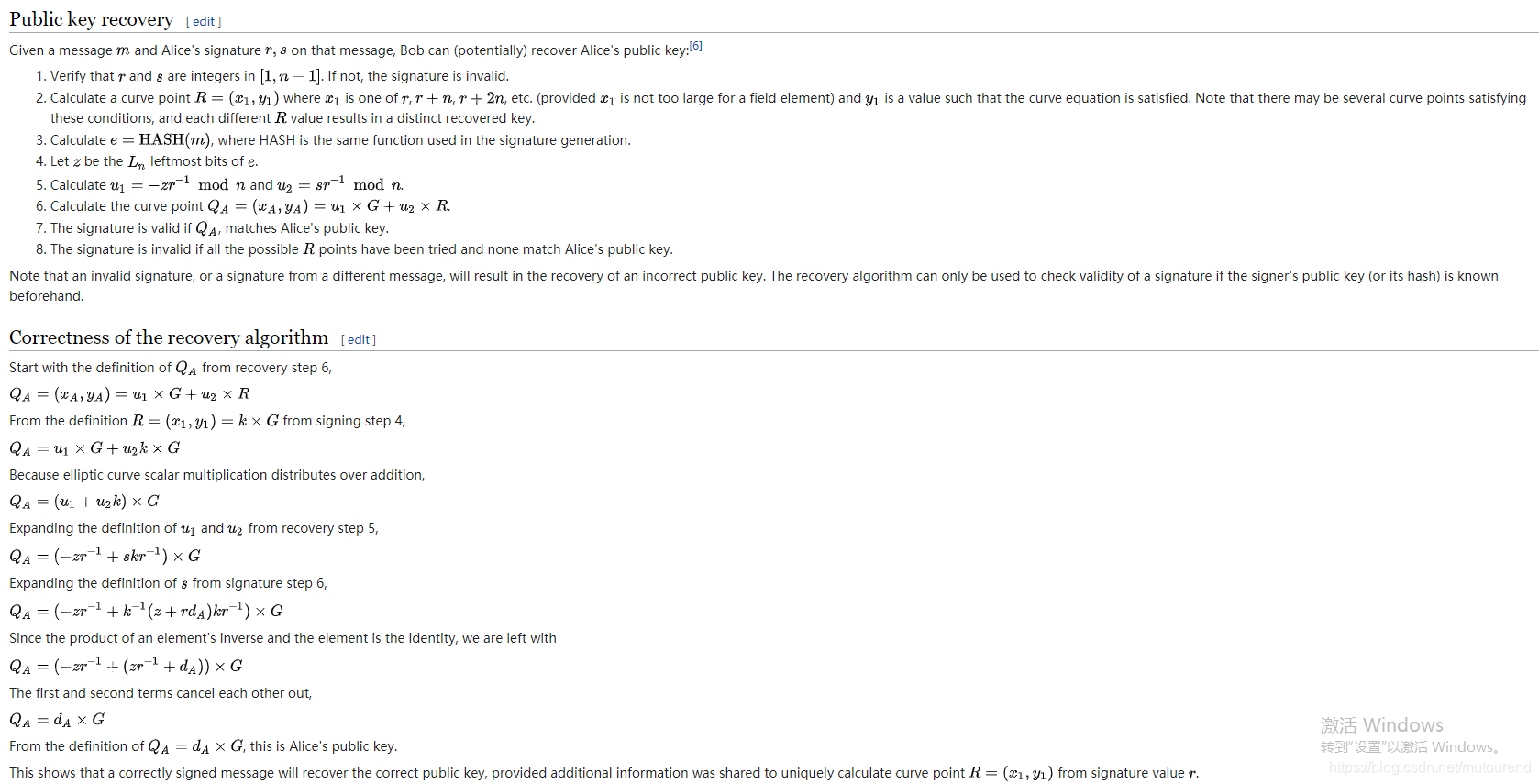
1.3 ECDSA的public key recovery

ECDSA也支持public key recovery算法，前提是提前知道签名方的公钥或者公钥hash值，否则有可能恢复出错误的公钥信息。

以太坊在0x01地址实现了ecrecover预编译合约，其函数原型为：

function ecrecover(bytes32 hash, bytes8 v, bytes32 r, bytes32 s) returns (address);

ecrecover会返回 根据给定的签名计算ECDSA recovery函数获得的地址address。
solidity合约中的调用示例为：

function recoverSignerFromSignature(uint8 v, bytes32 r, bytes32 s, bytes32 hash) external {
    address signer = ecrecover(hash, v, r, s);
    require(signer != address(0), "ECDSA: invalid signature");
}

在以太坊交易中，最后的65字节为ecdsa签名，依次为：

• 32字节的$r$
• 32字节的$s$
• 1字节的$v$：其中$v$为recovery identifier。根据以太坊黄皮书可知，$v$的取值范围为27~30（即0x1b~0x1e）。

参考资料

[1] What is ecrecover in Solidity?
[2] Ethereum Virtual Machine (EVM) ECRECOVER PRECOMPILED CONTRACT
[3] Ethereum Digital Signatures
[4] ECRecover and Signature Verification in Ethereum
[5] ECDSA Malleability
[6] Precompiled