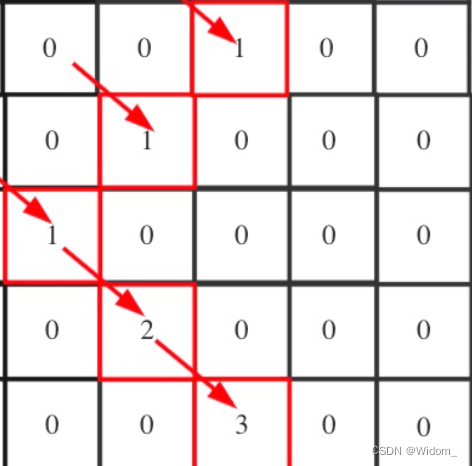
代码随想录算法训练营第五十二天 | 300. 最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组

news2024/11/26 22:48:42

1. 最长递增子序列

300. 最长递增子序列 - 力扣（LeetCode）

dp[i] 取决于 i 之前所有的dp

class Solution {
    public int lengthOfLIS(int[] nums) {
        // dp[i] 第 0 - i 位的递增子序列长度
        int length = nums.length;
        int[] dp =new int[length];
        Arrays.fill(dp, 1);

        int max = 1;
        for(int i = 1; i < length; i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j])
                    dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            max = Math.max(dp[i], max);
        }

        return max;
    }
}

2. 最长连续递增序列

674. 最长连续递增序列 - 力扣（LeetCode）

dp[i] 取决于 i-1 的dp

class Solution {
    public int findLengthOfLCIS(int[] nums) {

        int length = nums.length;
        int[] dp = new int[length];
        Arrays.fill(dp, 1);

        int max = 1;
        for(int i = 1; i < length; i++){
            if(nums[i] > nums[i-1]){
                dp[i] = dp[i-1] + 1;
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

3. 最长重复子数组

718. 最长重复子数组 - 力扣（LeetCode）

遍历两个数组，当前元素（及之前）的公共子数组取决于当前位置是否相等和前一位

注意，两个数组中有元素是第一个要初始化为 1

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        //dp[i][j] nums1[i] nums2[j] 前（包含）的最长公共子数组 * 当前位置必须相等
        int l1 = nums1.length;
        int l2 = nums2.length;
        int[][] dp = new int[l1][l2];
        int max= 0;

        for(int i = 0; i < l1; i++){
            for(int j = 0; j < l2; j++){
                if(nums1[i] == nums2[j]){ // * 当前位置必须相等
                    if( i == 0 || j == 0){
                        dp[i][j] = 1;
                    }else
                        dp[i][j] = dp[i-1][j-1] + 1;
                    max = Math.max(max, dp[i][j]);
                }
            }
        }
        return max;
    }
}