目录
- 前言
- RSA算法
- 代码实现
- 设计思路
- 结果示意
- Diffie-Hellman算法
- 代码实现
- 设计思路
- 结果示意
前言
信息安全是计算机科学的一个重要分支,它涉及到保护信息的机密性、完整性和可用性。信息加密是信息安全的一种常用手段,它通过使用一些数学算法和密钥,将明文转换为不易被破解的密文,从而防止未经授权的访问和篡改。本实验的目的是让学生了解基于密钥的加密方式的原理和实现方法,使用程序编写一个简单的加密和解密功能,并测试其效果。本实验分为两个部分:第一部分是理论学习,介绍基于密钥的加密方式的分类和特点,以及常见的加密算法;第二部分是实践操作,使用C语言编写一个基于对称密钥的加密和解密程序,并对不同长度的明文进行加密和解密,观察其运行时间和结果。
RSA算法
RSA算法是一种非对称加密算法,与对称加密算法不同的是,RSA算法有两个不同的密钥,一个是公钥,一个是私钥。
RSA公开密钥密码体制是一种使用不同的加密密钥与解密密钥,“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制 。
在公开密钥密码体制中,加密密钥(即公开密钥)PK是公开信息,而解密密钥(即秘密密钥)SK是需要保密的。加密算法E和解密算法D也都是公开的。虽然解密密钥SK是由公开密钥PK决定的,但却不能根据PK计算出SK 。
正是基于这种理论,1978年出现了著名的RSA算法,它通常是先生成一对RSA密钥,其中之一是保密密钥,由用户保存;另一个为公开密钥,可对外公开,甚至可在网络服务器中注册。为提高保密强度,RSA密钥至少为500位长。这就使加密的计算量很大。为减少计算量,在传送信息时,常采用传统加密方法与公开密钥加密方法相结合的方式,即信息采用改进的DES或IDEA对话密钥加密,然后使用RSA密钥加密对话密钥和信息摘要。对方收到信息后,用不同的密钥解密并可核对信息摘要 。
RSA是被研究得最广泛的公钥算法,从提出后经历了各种攻击的考验,逐渐为人们接受,普遍认为是目前最优秀的公钥方案之一。1983年麻省理工学院在美国为RSA算法申请了专利 。
RSA允许选择公钥的大小。512位的密钥被视为不安全的;768位的密钥不用担心受到除了国家安全管理(NSA)外的其他事物的危害;RSA在一些主要产品内部都有嵌入,像 Windows、网景 Navigator、 Quicken和 Lotus Notes 。
由于RSA算法1024位密钥面临严重的安全威胁,为保障电子认证服务安全应用,2016年12月5日,上海市密码管理局在其官方网站上发布公告,称从2017年1月1日起停止提供RSA算法1024位密钥对服务,并配合电子认证服务机构和应用单位做好应对措施,确保平稳过渡。
代码实现
#include<stdio.h>
#include<string.h>
#include <stdlib.h>
const int max=2e4;
int size;
int miwen[max];//为加密后的数字密文
char mingwen[max];
//判断两个数是否互为素数 eg:p和q e和 t
bool gcd(int p,int q)
{
int m,n;
if(q<p)
{
m=p; p=q; q=m; //将p换成p和q之间那个小的数
m=q%p; n=q/p; //辗转相除法求两个数的最大公因数
}
while(m!=0)
{
q=p; p=m; //将p换成p和q之间那个小的数
m=q%p; n=q/p;
}
if(m==0&&n==q)
{
printf("符合条件!\n");
return true;
}
else{
printf("不符合条件!请重新输入:\n");
return false;
}
}
//判断输入的p和q是不是素数
bool sushu(int s){
for(int i=2;i<s;i++){
if(s%i==0)
return false;
}
return true;
}
//求私钥d
int siyao(int e,int t) //t:欧拉函数
{
int d;
for(d=0;d<t;d++)
if(e * d % t==1)
return d;
}
//随机生成与 t互质的数e
int getrand(int p,int q)
{
int t=(p-1)*(q-1);
while(1)
{
int e=rand() % t;
if(gcd(e,t)==1)
return e;
// if(e<=2)
// e=3;
}
}
void jiami(int e,int n)
{
//先将符号明文转换成字母所对应的ascii码。
char mingwen[100]; //符号明文
printf("请输入明文:\n");
scanf("%s",mingwen);
size=strlen(mingwen);
int ming[strlen(mingwen)]; //定义符号明文
for(int i=0;i<strlen(mingwen);i++)
{
ming[i]=mingwen[i]; //将字母转换成对应的ascii码。
//printf("%d",mingwen[i]); //将字母转换成对应的ascii码。可以不输出
}
int flag=1; //miwen为加密后的数字密文
for(int i=0;i<strlen(mingwen);i++)
{
for(int j=0;j<e;j++)
{
flag=flag*ming[i]%n;
}
miwen[i]=flag;
flag=1;
}
printf("加密密文为:\n");
for(int i=0;i<strlen(mingwen);i++)
printf("%d",miwen[i]);
}
void jiemi(int d,int n)
{
int de_mingwen[size],flag=1;//解密后得到的数字明文(即ascii码)
char de_ming[size];//解密后得到的字符串明文
for(int i=0;i<size;i++)
{
for(int j=0;j<d;j++)
{
flag=flag*miwen[i]%n;
}
de_mingwen[i]=flag;
flag=1;
}
printf("解密后的明文为:\n");
for(int i=0;i<size;i++)
{
de_ming[i]=de_mingwen[i];
printf("%c",de_ming[i]);
}
}
int main()
{
int p,q,e,d,n,t,tep;
while(1)
{
printf("请输入p:",p);
scanf("%d",&p);
tep=sushu(p);
if(tep==0)
{
printf("p不是素数,请重新输入p!\n");
continue;
}
printf("请输入q:",q);
scanf("%d",&q);
tep=sushu(q);
if(tep==0)
{
printf("q不是素数,请重新输入q!\n");
printf("请输入q:",q);
scanf("%d",&q);
tep=sushu(q);
}
int n=p*q;
int t=(p-1)*(q-1);
tep=gcd(p,q);
if(tep==0) continue;
printf("t=(q-1)*(p-1)=%d\n",t);
e=getrand(p,q);
printf("公钥(e=%d n=%d)\n",e,n);
tep=(e,t);
d=siyao(e,t);
printf("私钥d=%d",d);
int a=0;
while(a!=3)
{
printf("\n-------------------------\n");
printf("1、加密\n");
printf("2、解密\n");
printf("3、退出");
printf("\n-------------------------\n");
scanf("%d",&a);
getchar();
if(a==1)
{
jiami(e,n);
}
else if(a==2)
{
printf("请输入密钥:");
scanf("%d",&d);2
jiemi(d,n);
}
else
return 0;
}
}
return 0;
}
设计思路
RSA加密算法的设计思路是基于数论的一些性质,主要有以下几个步骤:
首先,选择两个大的素数p和q,计算它们的乘积n,作为公钥的一部分。n的长度就决定了RSA算法的安全强度。
然后,计算n的欧拉函数φ(n),即小于n且与n互质的正整数的个数。根据数论的性质,φ(n) = (p-1)(q-1)。
接着,选择一个整数e,使得e与φ(n)互质,即最大公约数为1。e也作为公钥的一部分,用于加密信息。
然后,利用扩展欧几里得算法,求出e对于φ(n)的模反元素d,即满足ed ≡ 1 (mod φ(n))的整数d。d作为私钥的一部分,用于解密信息。
最后,将公钥(e, n)和私钥(d, n)分别保存或发布。加密信息m时,计算c = m^e mod n,得到密文c。解密密文c时,计算m = c^d mod n,得到明文m。
这样,RSA算法就实现了非对称加密和解密的过程,利用了素数分解和模反元素的难度来保证安全性。更多细节和证明可以参考这篇文章link或这篇文章link。
结果示意
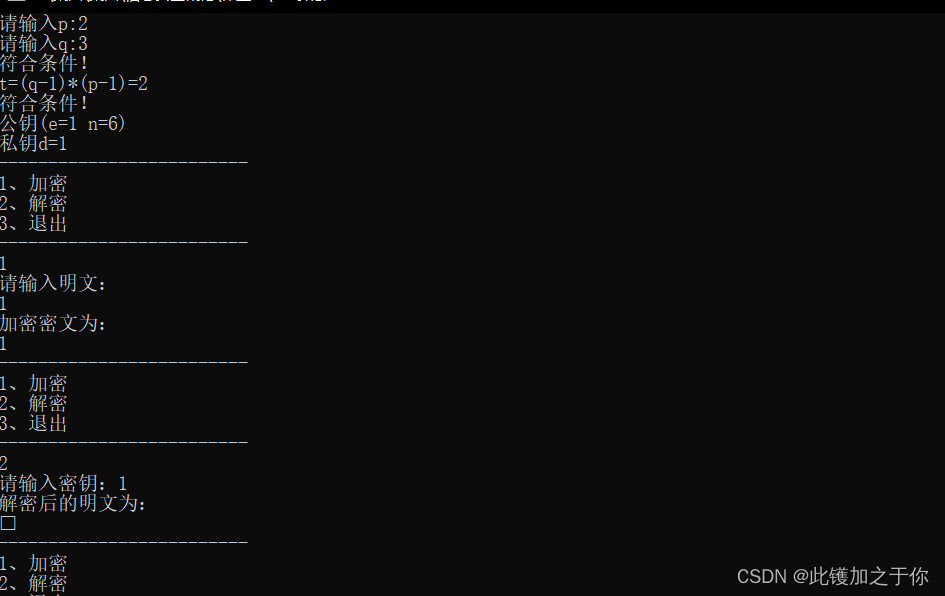
Diffie-Hellman算法
Diffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一,它使得通信的双方能在非安全的信道中安全的交换密钥,用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法,之后被应用于安全领域,比如 Https 协议的 TLS(Transport Layer Security) 和 IPsec 协议的 IKE(Internet Key Exchange) 均以 DH 算法作为密钥交换算法。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
// 定义一个函数,用于计算a的b次方模n的结果
int mod_pow(int a, int b, int n) {
int res = 1;
while(b > 0) {
if(b & 1) { // 如果b的最低位为1,则将res乘以a并取模
res = (res * a) % n;
}
a = (a * a) % n; // 将a平方并取模
b >>= 1; // 将b右移一位
}
return res;
}
// 定义一个函数,用于测试Diffie-Hellman加密算法
void test() {
// 定义公共参数p和g,这两个参数可以公开
int p = 23; // 一个大素数
int g = 5; // 一个小于p的整数
printf("Public parameters: p = %d, g = %d\n", p, g);
// 定义私有参数a和b,这两个参数不对外公开
int a = rand() % p; // A方随机选择一个小于p的整数作为私有参数
int b = rand() % p; // B方随机选择一个小于p的整数作为私有参数
printf("Private parameters: a = %d, b = %d\n", a, b);
// 定义公开参数A和B,这两个参数可以互相交换
int A = mod_pow(g, a, p); // A方计算g的a次方模p的结果作为公开参数
int B = mod_pow(g, b, p); // B方计算g的b次方模p的结果作为公开参数
printf("Public parameters: A = %d, B = %d\n", A, B);
// 定义共享密钥s,这个结果是相同的
int s1 = mod_pow(B, a, p); // A方计算B的a次方模p的结果作为共享密钥
int s2 = mod_pow(A, b, p); // B方计算A的b次方模p的结果作为共享密钥
printf("Shared secret: s1 = %d, s2 = %d\n", s1, s2);
}
// 主函数,调用测试函数
int main() {
test();
return 0;
}
设计思路
Diffie-Hellman密钥交换算法的设计思路是基于以下的想法:
两个通信方,比如说A和B,想要通过一个公开的不安全的信道,协商出一个共享的密钥,用于后续的对称加密通信。
他们首先选择一个大素数p和一个小于p的整数g,作为公共的参数,任何人都可以知道这两个数。
然后,A和B各自随机选择一个小于p的私有数a和b,作为自己的私钥,不对外公开。
接着,A和B分别计算g的a次方模p和g的b次方模p的结果,作为自己的公钥,互相交换这两个数。
最后,A和B利用对方的公钥和自己的私钥,计算出g的ab次方模p或者g的ba次方模p的结果,作为共享的密钥。由于模幂运算的性质,这两个结果是相同的。
这样,A和B就通过两轮信息交换,实现了密钥协商的过程。由于离散对数问题和计算性Diffie-Hellman问题的难度,即使有人知道了p、g、g的a次方模p和g的b次方模p这四个数,也很难推算出a、b或者g的ab次方模p。因此,这个算法可以保证密钥的安全性。更多细节和证明可以参考这篇文章tink或这篇文章tink。
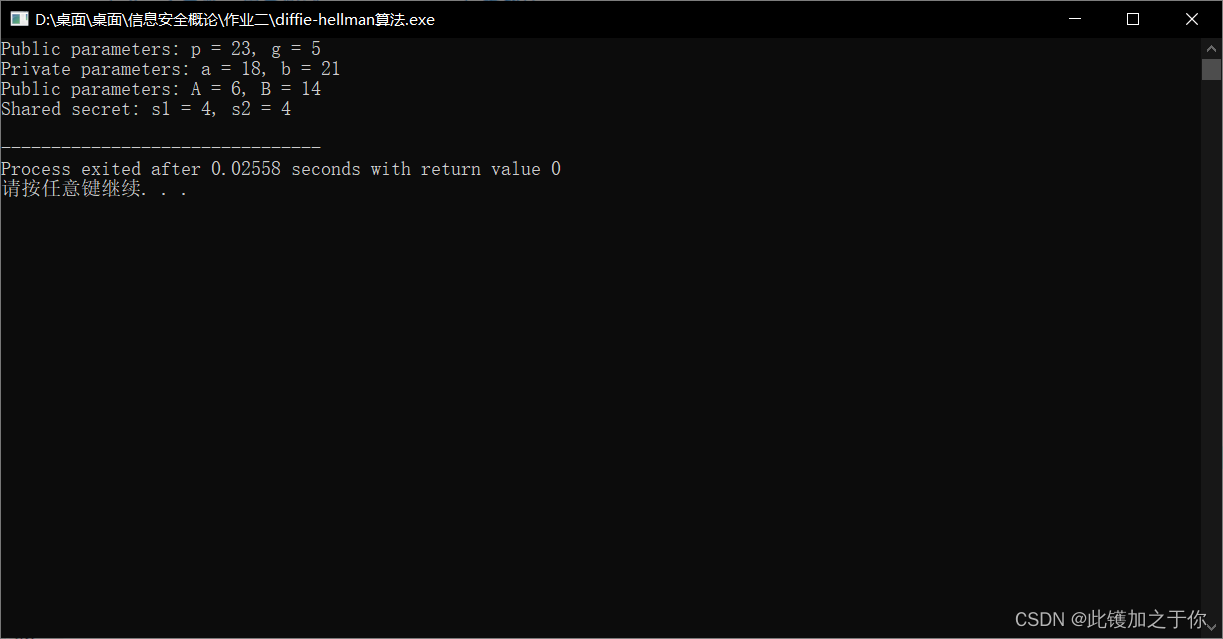
结果示意
![P1525 [NOIP2010 提高组] 关押罪犯(并查集)](https://img-blog.csdnimg.cn/05396e613bd146bbbaa2fbc84a2b1823.png)