目录
一、实验介绍
二、实验环境
1. 配置虚拟环境
2. 库版本介绍
3. IDE
三、实验内容
0. 导入必要的工具
1. 生成邻接矩阵simulate_G:
2. 计算节点的聚集系数 CC(G):
3.计算节点的介数中心性 BC(G)
4. 计算节点的度中心性 DC(G)
5. 综合centrality(G)
6. 代码整合
一、实验介绍
本实验实现了计算图网络中节点的中心性指标,包括聚集系数、介数中心性、度中心性等
二、实验环境
本系列实验使用了PyTorch深度学习框架,相关操作如下(基于深度学习系列文章的环境):
1. 配置虚拟环境
深度学习系列文章的环境
conda create -n DL python=3.7 conda activate DLpip install torch==1.8.1+cu102 torchvision==0.9.1+cu102 torchaudio==0.8.1 -f https://download.pytorch.org/whl/torch_stable.html
conda install matplotlibconda install scikit-learn新增加
conda install pandasconda install seabornconda install networkxconda install statsmodelspip install pyHSICLasso注:本人的实验环境按照上述顺序安装各种库,若想尝试一起安装(天知道会不会出问题)
2. 库版本介绍
| 软件包 | 本实验版本 | 目前最新版 |
| matplotlib | 3.5.3 | 3.8.0 |
| numpy | 1.21.6 | 1.26.0 |
| python | 3.7.16 | |
| scikit-learn | 0.22.1 | 1.3.0 |
| torch | 1.8.1+cu102 | 2.0.1 |
| torchaudio | 0.8.1 | 2.0.2 |
| torchvision | 0.9.1+cu102 | 0.15.2 |
新增
| networkx | 2.6.3 | 3.1 |
| pandas | 1.2.3 | 2.1.1 |
| pyHSICLasso | 1.4.2 | 1.4.2 |
| seaborn | 0.12.2 | 0.13.0 |
| statsmodels | 0.13.5 | 0.14.0 |
3. IDE
建议使用Pycharm(其中,pyHSICLasso库在VScode出错,尚未找到解决办法……)
win11 安装 Anaconda(2022.10)+pycharm(2022.3/2023.1.4)+配置虚拟环境_QomolangmaH的博客-CSDN博客https://blog.csdn.net/m0_63834988/article/details/128693741https://blog.csdn.net/m0_63834988/article/details/128693741
三、实验内容
0. 导入必要的工具
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt1. 生成邻接矩阵simulate_G:
def simulate_G(d):
B = np.random.binomial(1, 0.3, size=(d, d))
return np.triu(B, 1) + np.triu(B, 1).T
- 生成一个随机的邻接矩阵表示的图,其中节点数为 d。
- 使用numpy 库的
random.binomial函数生成一个具有一定概率连接的邻接矩阵 - 通过
triu函数提取出上三角部分(不包括对角线),然后与其转置相加,得到一个无向图的邻接矩阵。
- 使用numpy 库的
2. 计算节点的聚集系数 CC(G):
def CC(G):
cc = {}
# single_source_dijkstra_path_length 从点i到其他点的最短路径长度
# nx.single_source_dijkstra_path(G_nx, i)
for i in range(G.shape[0]):
pre_num = 0
for k, v in nx.single_source_dijkstra_path_length(G_nx, i).items():
pre_num += v
cc[len(cc)] = (G.shape[0] - 1) / pre_num
return cc 通过遍历图中的每个节点,使用 networkx 库的 single_source_dijkstra_path_length 函数计算该节点到其他节点的最短路径长度,并将这些路径长度求和。然后,通过计算 (节点总数 - 1) / 最短路径长度之和,得到该节点的聚集系数。
3. 计算节点的介数中心性 BC(G)
def BC(G):
bc_res = {}
bc = [0.] * G.shape[0]
for i in range(G.shape[0]):
for j in range(G.shape[0]):
shortest_paths = list(nx.all_shortest_paths(G_nx, i, j))
for v in shortest_paths:
for pre in v[1:-1]:
bc[pre] += 1. / len(shortest_paths)
for i in range(G.shape[0]):
bc_res[i] = bc[i] / ((G.shape[0] - 1) * (G.shape[0] - 2))
return bc_res
遍历图中的每对节点,使用 networkx 库的 all_shortest_paths 函数找到它们之间的所有最短路径,并对每条路径上的中间节点进行计数。然后,通过计算每个节点的介数值(即通过该节点的最短路径数除以所有最短路径数的总和),得到节点的介数中心性。
4. 计算节点的度中心性 DC(G)
def DC(G):
dc_res = {}
degree = np.sum(G, axis=1)
dc = degree / (G.shape[0] - 1)
for index, item in enumerate(dc):
dc_res[index] = item
return dc_res计算节点的度中心性(degree centrality)。首先计算每个节点的度(与其相连的边的数量),然后将度除以节点总数减去 1,得到节点的度中心性。
5. 综合 centrality(G)
def centrality(G):
cc = CC(G)
bc = BC(G)
dc = DC(G)
return dc, cc, bc
这个函数是一个综合函数,用于计算节点的三种中心性指标:度中心性、聚集系数和介数中心性。它调用上述三个函数,并返回这些中心性指标的字典。
6. 代码整合
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
def simulate_G(d):
B = np.random.binomial(1, 0.3, size=(d, d))
return np.triu(B, 1) + np.triu(B, 1).T
def CC(G):
cc = {}
# single_source_dijkstra_path_length 从点i到其他点的最短路径长度
# nx.single_source_dijkstra_path(G_nx, i)
for i in range(G.shape[0]):
pre_num = 0
for k, v in nx.single_source_dijkstra_path_length(G_nx, i).items():
pre_num += v
cc[len(cc)] = (G.shape[0] - 1) / pre_num
return cc
def BC(G):
bc_res = {}
bc = [0.] * G.shape[0]
for i in range(G.shape[0]):
for j in range(G.shape[0]):
shortest_paths = list(nx.all_shortest_paths(G_nx, i, j))
for v in shortest_paths:
for pre in v[1:-1]:
bc[pre] += 1. / len(shortest_paths)
for i in range(G.shape[0]):
bc_res[i] = bc[i] / ((G.shape[0] - 1) * (G.shape[0] - 2))
return bc_res
def DC(G):
dc_res = {}
degree = np.sum(G, axis=1)
dc = degree / (G.shape[0] - 1)
for index, item in enumerate(dc):
dc_res[index] = item
return dc_res
def centrality(G):
cc = CC(G)
bc = BC(G)
dc = DC(G)
return dc, cc, bc
if __name__ == '__main__':
# np.random.seed(0)
# G = simulate_G(8)
G = np.array([[0, 1, 0, 1, 1],
[1, 0, 1, 0, 0],
[0, 1, 0, 0, 1],
[1, 0, 0, 0, 1],
[1, 0, 1, 1, 0]
])
G_nx = nx.from_numpy_matrix(G)
nx.draw_kamada_kawai(G_nx, with_labels=True)
plt.show()
dc, cc, bc = centrality(G)
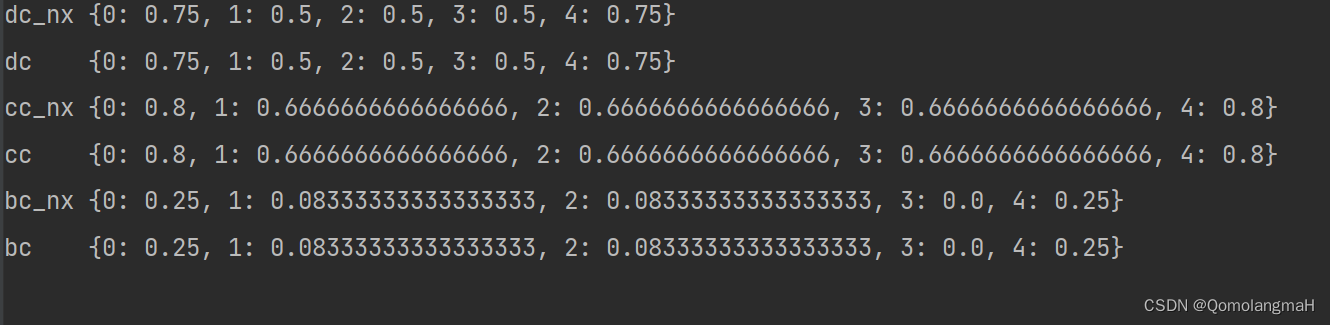
print("dc_nx", nx.degree_centrality(G_nx))
print("dc ", dc)
print("cc_nx", nx.closeness_centrality(G_nx))
print("cc ", cc)
print("bc_nx", nx.betweenness_centrality(G_nx))
print("bc ", bc)


![[DS资源推荐] Data Structure 严书配套代码](https://img-blog.csdnimg.cn/634d16b4c5ad4e7a9e676876057c75c0.png)





![模拟实现map/set[改编红黑树实现map/set容器底层]](https://img-blog.csdnimg.cn/b6cfeb7e27954d3ea12e615533b5fc29.png)