原文链接：https://arxiv.org/abs/2307.02270

1. 引言

  目前的从单目相机生成伪传感器表达的方法依赖预训练的深度估计网络。这些方法需要深度标签来训练深度估计网络，且伪立体方法通过图像正向变形合成立体图像，会导致遮挡区域的像素伪影、扭曲、孔洞。此外，特征级别的伪立体图生成很难直接应用，且适应度有限。
  那么如何绕过深度估计，在图像层面设计透视图生成器呢？和GAN相比，扩散模型有更简单的结构、更少的超参数和更简单的训练步骤，但目前没有关于3D目标检测伪视图生成的研究。
  本文设计单一视图扩散模型（SVDM）进行伪视图合成。SVDM假设已知左视图图像，将高斯噪声替换为左图像素，并逐渐扩散右图像素到全图。由于立体图像细微的视差，仅使用很少的步骤就能产生不错的结果。SVDM不使用深度真值，且能端到端训练。

3. 方法

3.1 准备知识

3.1.a 立体3D检测器

  可分为3类：只需要立体图像训练的模型（如Stereo R-CNN）、需要额外深度真值训练的模型（YOLOStereo3D）和基于体积网格的模型（如LIGA-Stereo）。

3.1.b 去噪扩散概率模型（DDPM）

  详见扩散模型（Diffusion Model）简介。DDPM的目标是最优化置信下限（ELBO）。多数条件扩散模型保留了扩散过程，并将条件$y$插入训练目标中：$${\mathbb{E}}_{t,x_0,ϵ}[\Vert ϵ-{ϵ}_{\theta }(x_t,y,t){\Vert }_2^2]$$  但由于$p(x_t|y)$没有显式地出现在训练目标中，要保证扩散模型能学到期望的条件分布是很困难的。

3.2 单一视图扩散模型

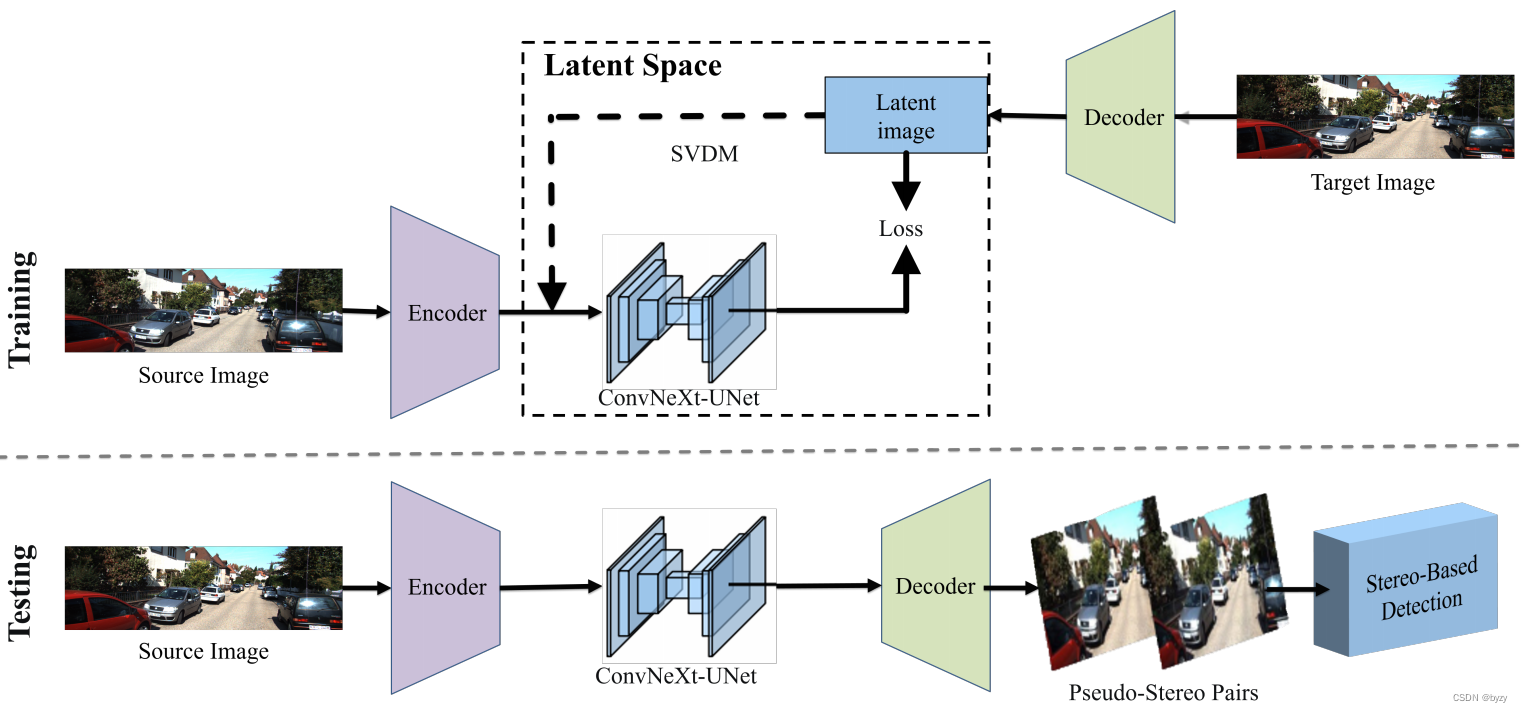
  本模型将新视图生成任务视为基于扩散模型的、图像到图像（I2I）的转换任务。本文的方法如下图所示，包含3种扩散模型方法：高斯噪声操作器、视图图像操作器和一步生成。

3.2.a 高斯噪声操作器

  为了学习两个视图域之间的变换，根据BBDM，本文使用布朗桥扩散过程而非DDPM方法。
  布朗桥过程是连续时间随机模型，其中扩散过程中的概率分布是以起始状态和终止状态为条件的。记起始状态为$x_0\sim q_{data}(x_0)$，终止状态为$x_T$，则布朗桥扩散过程的状态分布为$$q_{BB}(x_t|x_0,y)=\mathcal{N}(x_t;(1-m_t)x_0+m_{t}y,{\delta }_{t}I)$$其中$m_t=t/T$，${\delta }_t$为方差。为避免方差过大导致无法训练，使用下列方差调度：$${\delta }_t=s[1-((1-m_t{)}^2+m_t^2)]=2s(m_t-m_t^2)$$其中$s$控制样本的多样性，默认为1。
  正向过程如下：当$t=0$时，$m_t=0$，此时均值为$x_0$，方差为0；当$t=T$时，$m_t=1$，此时均值为$y$，方差为0。中间过程按下式计算：$$x_t=(1-m_t)x_0+m_{t}y+\sqrt{{\delta }_t}ϵ$$其中$ϵ\sim \mathcal{N}(0,I)$。用$t-1$替换上式中的$t$，两式相减得到转移概率：$$q_{BB}(x_t|x_{t-1},y)=\mathcal{N}(x_t;\frac{1-m_t}{1-m_{t-1}}{x}_{t-1}+(m_t-\frac{1-m_t}{1-m_{t-1}}{m}_{t-1})y,{\delta }_{t|t-1}I)$$其中$${\delta }_{t|t-1}={\delta }_t-{\delta }_{t-1}\frac{(1-m_t{)}^2}{(1-m_{t-1}{)}^2}$$  逆过程从已知视图出发，逐步得到目标视图的分布。即基于$x_t$预测$x_{t-1}$：$$p_{\theta }(x_{t-1}|x_t,y)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\tilde{\delta }}_{t}I)$$其中${\mu }_{\theta }(x_t,t)$是预测噪声的均值，由神经网络基于极大似然准则估计。${\tilde{\delta }}_t$为每步噪声的方差，解析形式为${\tilde{\delta }}_t=\frac{{\delta }_{t|t-1}{\delta }_{t-1}}{{\delta }_t}$。
  完整的训练和推断过程如下：

BBDM的训练算法

1. 采样数据对$x_0\sim q(x_0),y\sim q(y)$；
2. 均匀采样时间 t ∈ { 1 , 2 , ⋯   , T } t\in\{1,2,\cdots,T\} t∈{1,2,⋯,T}；
3. 采样高斯噪声$ϵ\sim \mathcal{N}(0,I)$；
4. 正向扩散：$x_t=(1-m_t)x_0+m_{t}y+\sqrt{{\delta }_t}ϵ$；
5. 计算$\Vert m_t(y-x_0)+\sqrt{{\delta }_t}ϵ-{ϵ}_{\theta }(x_t,t){\Vert }^2$的梯度。

BBDM的采样算法：

1. 采样条件输入$x_T=y\sim q(y)$；
2. 从$t=T$开始，进行下面的过程直到$t=1$：
     采样$z\sim \mathcal{N}(0,I)$
     计算$x_{t-1}=c_{xt}{x}_t+c_{yt}y-c_{ϵt}{ϵ}_{\theta }(x_t,t)+\sqrt{{\tilde{\delta }}_t}z$；
3. $t=1$时，计算$x_0=c_{x1}{x}_1+c_{y1}y-c_{ϵ1}{ϵ}_{\theta }(x_1,1)$。

3.2.b 视图图像操作器

  布朗桥扩散模型引入了额外的超参数。本文提出基于视图图像操作器的方法，将目标图像视为特殊噪声，迭代地将目标图像转换为源图像。给定初始状态$x_0$和目标状态$y$，中间状态$x_t$可写为：$$x_t=\sqrt{{\alpha }_t}{x}_0+\sqrt{1-{\alpha }_t}y$$与常规的添加噪声过程不同，此处添加的为逐步增加权重的新视图图像。采样过程如下所示：

1. 输入源图像$x_T$；
2. 从$t=T$开始，进行下面的过程直到$t=0$：
     $x_0\le f(x_t,t)$
     $x_{t-1}=x_s-D(x_0,t)+D(x_0,t-1)$

(关于该方法的采样算法，原文中用到的符号应该是有问题且欠缺解释的，这里仅能猜测原文的$s$以及$i$实际均应为$t$)

  ${\alpha }_t$的调度如下：$${\alpha }_t=\frac{f(t)}{f(0)},f(t)=\cos (\frac{t/T+s}{1+s}\cdot \frac{\pi }{2}{)}^2$$与线性调度相比，余弦调度添加目标视图更慢。

3.2.c 加速采样和一步生成

  由于扩散概率模型通常会需要大量步数采样，为加速推断过程，本文提出两种方法：一是添加高阶求解器引导DPM采样，二是引入一步生成方法。
  加速采样：与DDIM的基本思想相似，BBDM也可以在使用非马尔科夫过程的同时，保持和马尔科夫推断过程有相同的边沿分布。
  给定 { 1 , 2 , ⋯   , T } \{1,2,\cdots,T\} {1,2,⋯,T}的长为$S$的子序列 { T 1 , T 2 , ⋯   , T S } \{T_1,T_2,\cdots,T_S\} {T1​,T2​,⋯,TS​}，推断过程可由隐变量的子集 { x T 1 , x T 2 , ⋯   , x T S } \{x_{T_1},x_{T_2},\cdots,x_{T_S}\} {xT1​​,xT2​​,⋯,xTS​​}定义：$$q_{BB}(x_{T_{s-1}}|x_{T_s},x_0,y)=\mathcal{N}((1-m_{T_{s-1}})x_0+m_{T_{s-1}}+\frac{\sqrt{{\delta }_{T_{s-1}}-{\sigma }_{T_s}^2}}{\sqrt{{\delta }_{T_s}}}(x_{T_s}-(1-m_{T_s})x_0-m_{T_s}y),{\sigma }_{T_s}^{2}I)$$
  一步生成：目标是不牺牲迭代细化优势的情况下进行一步生成。这些优势包括能平衡计算和质量，以及零样本数据编辑的能力。该方法建立在连续时间扩散模型概率流常微分方程（ODE）的基础上，其轨迹平滑地从数据分布转变为可处理的噪声分布。使用一个模型学习将任意步骤上的点映射到轨迹的起点，这样模型有自我一致性（即同一条轨迹上的点会被映射到相同的起点）。
  一致性模型能在一次网络评估中将随机噪声向量（ODE轨迹的终点，$x_T$）转变为数据样本（ODE轨迹的起点，$x_0$）。通过多步连接一致性模型的输出，能用更多的计算提高样本质量并进行零样本数据编辑，从而保持迭代细化的优势。

3.3 网络结构

  根据隐式扩散模型（LDM），SVDM在隐空间而非原始像素空间内进行生成学习以减小计算。
  LDM使用预训练的VAE编码器$E$将图像$v\in {\mathbb{R}}^{3\times H\times W}$编码为隐式嵌入$z=E(v)\in {\mathbb{R}}^{c\times h\times w}$。其前向过程逐渐向$z$加入噪声，逆过程去噪以预测$z$。最后，LDM使用预训练的VAE解码器$D$解码$z$，得到高分辨率图像$v=D(z)$。VAE的编码器和解码器在训练和推断时均保持固定，而由于$h<H,w<W$，在低分辨率隐空间内扩散比在像素空间扩散更高效。本文的方法类似，给定从域$A$中采样的图像$I_A$，首先提取隐特征$L_A$，然后进行SVDM过程，将$L_A$映射到相应的、域$B$内的隐式表达$L_{A\to B}$。最后使用预训练的VQGAN的解码器生成图像$I_{A\to B}$。
  SVDM模型沿通道维度连接两张图像，并使用标准的U-Net结构和Conv-NeXt残差块进行上下采样，以达到大感受野获取上下文信息。此外，还在不同分辨率下引入注意力块，因为全局交互能大幅提高重建质量。

3.4 损失函数

  损失函数包含3项：RGB L1损失，RGB SSIM损失与感知损失。

3.4.a RGB L1损失与SSIM损失

  L1损失与SSIM损失如下：$$\begin{gathered} {\mathcal{L}}_{L1}=\frac{1}{3HW}\sum |{\hat{I}}_{tgt}-I_{tgt}| \\ {\mathcal{L}}_{ssim}=1-SSIM({\hat{I}}_{tgt},I_{tgt}) \end{gathered}$$其中${\hat{I}}_{tgt}$与$I_{tgt}$分别为像素通道的预测值和真实值。

3.4.b 感知损失

  基于过去的工作，感知损失通过强制局部真实性确保重建约束于图像流形，且避免了仅依赖RGB损失引入的模糊。$${\mathcal{L}}_{latent}=\frac{1}{2}\sum _{j=1}^J[(u_j^2+{\sigma }_j^2)-1-\log {\sigma }_j^2]$$

4. 实验

4.4 基于单一图像的视图合成结果

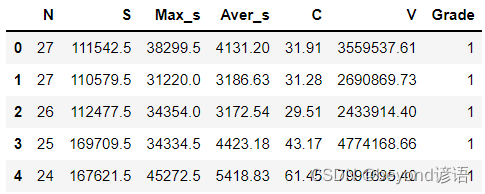
  定量结果：本文的方法在PSNR指标上能超过SotA，但SSIM和LPIPS指标略低于SotA。
  定性结果：可视化表明，本文的方法能生成更真实的图像，有更小的扭曲和伪影。这表明本文的方法有能力建模复杂场景的几何和纹理。

4.5 3D目标检测结果

  定量结果：实验表明，SVDM在使用BBDM的情况下，能超过大多数先进方法。使用视图扩散方法能进一步提升性能，这表明视图结构在3D目标检测上有更好的泛化能力。
  此外，虽然不能完全超过SotA，SVDM在困难物体的检测上有更好的性能。简单物体性能较差的原因可能是有限的约束。背景和障碍物都不可避免地干扰了新视图生成。ConvNeXt-UNet结构能在一定程度上减轻此问题，但并不完美。

4.3 消融研究

  行人和自行车的3D检测结果：由于样本数量少，行人和自行车的检测比汽车的检测更加困难。但本文的方法能在几乎所有难度上超过SotA。

5. 结论和未来展望

  目前，SVDM的一个缺点是不能端到端训练。