第一讲 基础算法

快速排序

归并排序

二分

整数二分模板

关键------画一个仅有整数的一维横轴

bool check(int x) {/* ... */} // 检查x是否满足某种性质   // check()判断mid是否满足性质




// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)//右半区间的左端点==mid
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid; 
        else l = mid + 1;
    }
    return l;
}




// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)//左半区间的右端点==mid 
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;//当l=mid时答案在右区间，为了避免进入死循环————[m,r]更新过后m会一直等于m（m+1==r的情况） 所以要上取整 
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

AcWing 789. 数的范围(整数二分法)

AcWing 789. 数的范围

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 100010;

int n,q;
int a[N];
int main()
{
    cin>>n>>q;
    for (int i = 0; i < n; i ++ ) cin >> a[i];

    while(q--)
    {
        int k;
        cin >> k;
        int l=0,r=n-1;
        while(l<r)//右半区间的左端点
        {
            int mid=(l+r)/2;//l+r>>1;
            if(a[mid]<k)//此处的符号<不能变
                l=mid+1;
            else
                r=mid;//此时a[mid]>=k
                
        }
        if(a[l]!=k)//此时说明该序列中不含有k 
           cout<<-1<<" "<<-1<<endl; 
        else
            {
                cout <<l<<" ";
                l=0,r=n-1;
                while (l<r)//左半区间的右端点
                {
                    int mid=(l+r+1)/2;
                    if(a[mid]<=k)//此处的符号<=不能变
                        l=mid;
                    else
                        r=mid-1;//此时a[mid]>k
                        
                }
                cout <<l<<endl;
            }
            
        
    }
    
    
}
 /*
为什么需要+1？
原因是如果不加上1，那么mid得到的是下取整的数，
那么有可能[m,r]更新过后m会一直等于m（m+1==r的情况）会陷入死循环。
*/

AcWing 1236.递增三元组

递增三元组

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=1e5+10;
const int INF=0x3f3f3f3f;
int n;
int a[N],b[N],c[N];
LL res;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i]; 
	for(int i=1;i<=n;i++) cin>>b[i]; 
	for(int i=1;i<=n;i++) cin>>c[i]; 
	 
	//由于二分的前提是单调序列 所以预先对a b c排序 直接sort
	sort(a+1,a+n+1);
	sort(b+1,b+n+1);
	sort(c+1,c+n+1);
	
		
	for(int i=1;i<=n;i++)
	{
	//直接用STL中的两个二分函数解决
	LL x = (lower_bound(a+1,a+1+n,b[i])-(a+1));     //在数组a中找比b[i]小的数  的个数x 
    LL y = n-(upper_bound(c+1,c+1+n,b[i])-(c+1)); //在数组c中找比b[i]大的数  的个数y 
    res+=x*y;
	}
	cout<<res<<endl;
	return 0;
 } 

AcWing 730. 机器人跳跃问题

AcWing 730. 机器人跳跃问题
视频讲解

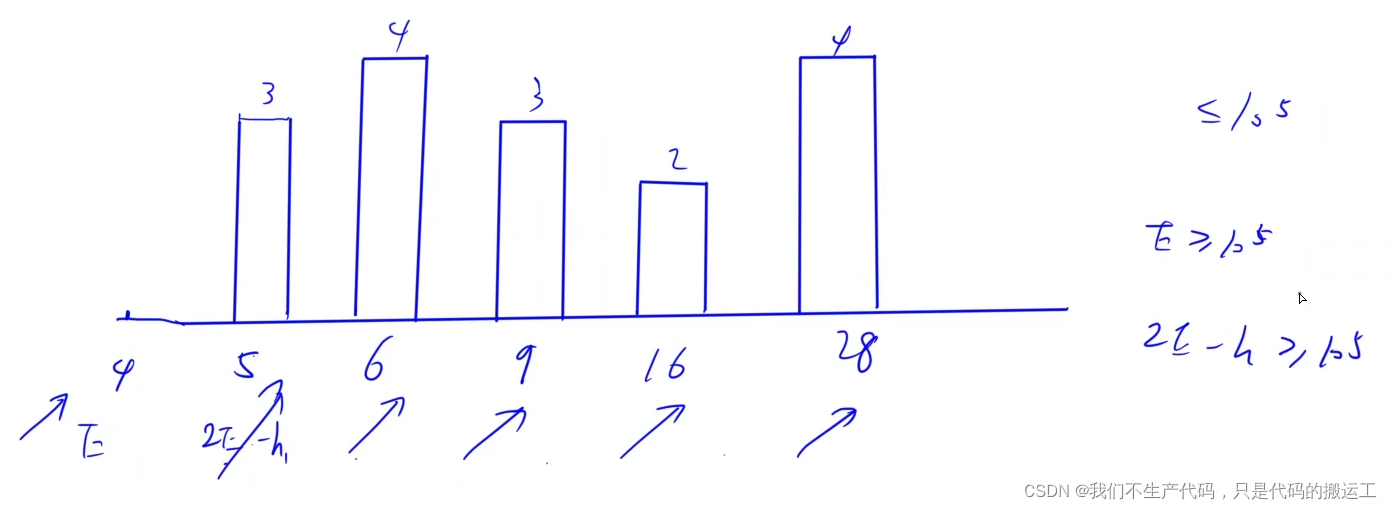
且答案具有单调性，证明可以使用二分法解决
易知，h[0]越大，整个过程中所有的e越大，因此，具有单调性
剪枝 ：因为h[i]的范围是 [ 1 , 1 e 5 ] [1,1e5] [1,1e5]，因此根据公式，只要在某一状态下e达到1e5，之后一定递增或不变，直接返回true

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5+10;
int n;
int h[N];
bool check(int mid)
{
    for (int i = 1; i <= n; i ++ )
    {
        mid=mid*2-h[i];//每次登录到新的柱子后的能量
        if(mid<0)  return false;//说明下一个柱子一定跳不上去
        if(mid>=N)  return true;//此时后面一定全部满足
    }
    return true;
}
int main()
{
    cin>>n;
    for (int i = 1; i <= n; i ++ )cin>>h[i];
    int l=0,r=N;
    while(l<r)
    {
        int mid=(l+r)/2;
        if(check(mid)) r=mid;
        else
            l=mid+1;
    }
    cout <<l<<endl;
    return 0;
    
}

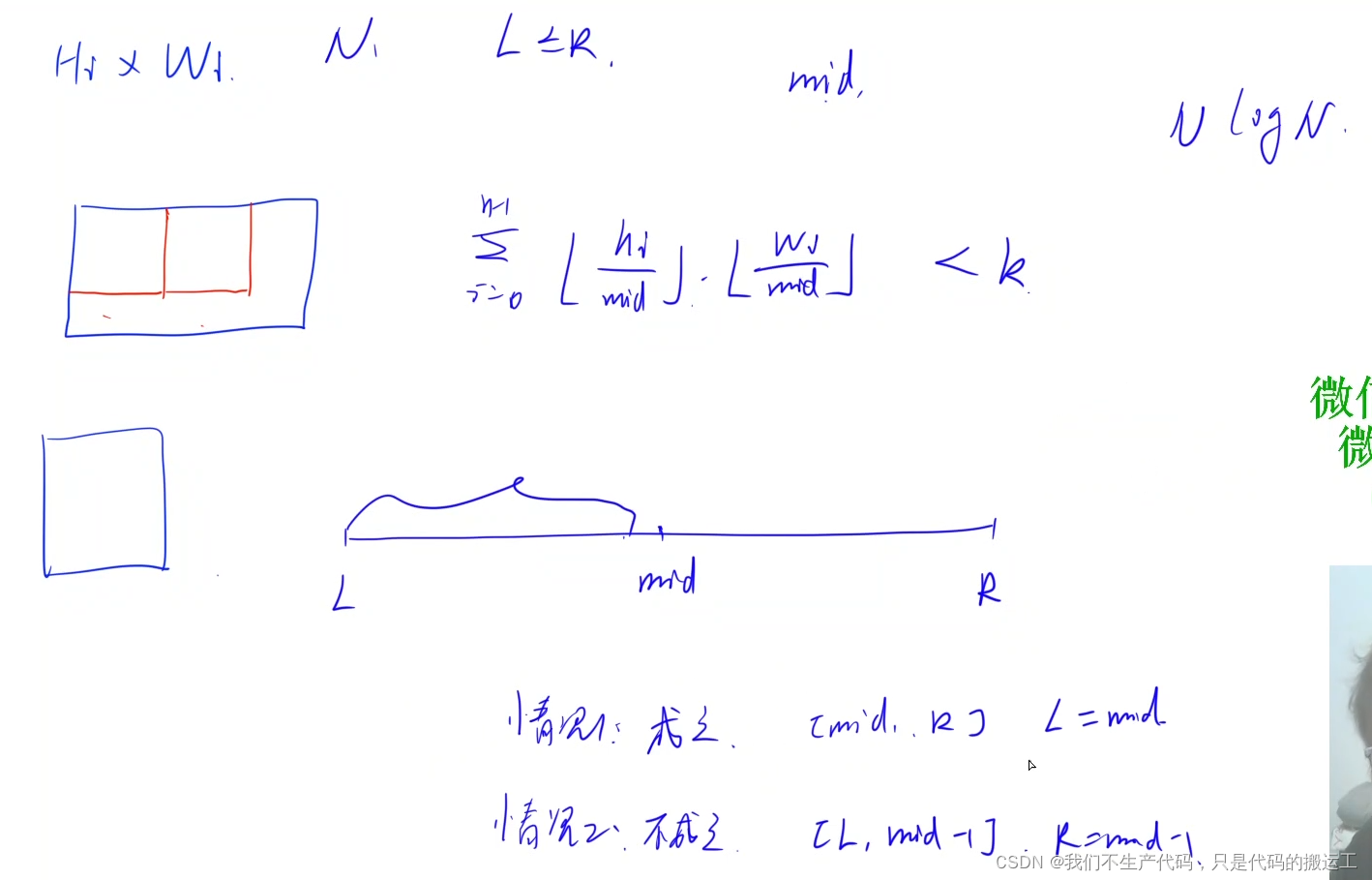
AcWing 1227. 分巧克力

AcWing 1227. 分巧克力
视频讲解

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5+10;
int n;
int k;
int h[N],w[N];
bool check(int mid)
{
    LL res=0;//表示可以切割出来的矩形个数
    for(int i=0;i<n;i++)//枚举一下所有的巧克力块
    {
        res+=(LL)(h[i]/mid)*(w[i]/mid);
        if(res>=k)
            return true;
    }
    return false;
    
}
int main()
{
    cin>>n>>k;
    for(int i=0;i<n;i++)
    {
        cin>>h[i]>>w[i];
    }
    int l=1,r=1e5;
    while(l<r)
    {
        int mid=(l+r+1)/2;//此时 mid属于有区间，为了避免死循环
        if(check(mid))
            l=mid;
        else
            r=mid-1;
    }
    cout<<l<<endl;
    return 0;
}

AcWing 1221. 四平方和(二分法/哈希)

AcWing 1221. 四平方和

视频讲解

完全暴力写法 一定会超时

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 2500010;

int n;

int main()
{
    cin >> n;
    for (int a = 0; a * a <= n; a ++ )
        for (int b = a; a * a + b * b <= n; b ++ )
            for (int c = b; a * a + b * b + c * c <= n; c ++ )
            {
                int t = n - a * a - b * b - c * c;
                int d = sqrt(t);//开平方
                if (d * d == t)
                {
                    printf("%d %d %d %d\n", a, b, c, d);
                    return 0;
                }
            }
}

//超时 

哈希表的写法，但超时了

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second

const int N = 5e6+10;
unordered_map<int, PII> S;
int n;
int main()
{
    cin >> n;
   for(int c=0;c*c<=n;c++)
        for(int d=c;d*d<=n;d++)
        {
            int t=c*c+d*d;
            if(S.count(t)==0)//如果之前没有出现过此结果，则添加入
                S[t]={c,d};
        }
    for(int a=0;a*a<=n;a++)
        for(int b=a;b*b<=n;b++)
        {
            int t=n-a*a-b*b;
            if(S.count(t))
            {
                 cout<<a<<" "<<b<<" "<<S[t].x<<" "<<S[t].y<<endl;
                 return 0;
            }
               
            
        }
    return 0;
}

蓝桥杯-扫地机器人 (二分+贪心)

扫地机器人（二分+贪心）
AcWing3176.扫地机器人

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,k;
int w[N];

bool check(int x)
{
	int total=0;
	for(int i=1;i<=k;i++)
	{
		if(total>=w[i]-x)
		{
			if(total>=w[i])
				total=w[i]+x;
			else
				total+=x;
		}
		else
			return false;
	}
	if(total>=n)
		return true;
	else
		return false;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=k;i++)	cin>>w[i];
	sort(w+1,w+k+1);
	int l=0,r=n;
	while(l<r)
	{
		int mid=l+r>>1;
		if(check(mid))
			r=mid;
		else
			l=mid+1;
	}
	cout<<(l-1)*2<<endl;
	return 0;
}

AcWing 790. 数的三次方根(浮点二分法)

AcWing 790. 数的三次方根

#include <iostream>
#include <cstring>
#include <algorithm>
#include<bits/stdc++.h>
using namespace std;

double n;

int main()
{
    cin>>n;
    double l=-10000,r=10000;//答案ans范围的初始化
    while(r-l>=1e-8)
    {
        double mid = (l+r)/2;//中间值
        
        if(mid*mid*mid<n)
            l=mid;
        else
            r=mid;
    }//二分过程参考
    printf("%.6lf",l);//记得保留小数
    return 0;
}

AcWing 680. 剪绳子(浮点二分法)

AcWing 680. 剪绳子

视频讲解

思路分析+代码注释详解

高精度

前缀

一维前缀和

AcWing 795. 前缀和

前缀和算法
预处理时间复杂度：O(n)
求前缀和时间复杂度：O(1)
用空间来换取时间
前缀和算法（前缀和的下标都从1开始，避免出现越界）
算法理论：
前缀和其实就是 动态规划 的思想

acwing 795. 一维前缀和

/*
一维前缀和 ( O(1) 的时间求出一段区间的和 )
b[i] = a[1] + a[2] + … a[i]=b[i-1]+a[i] 
a[l] + … + a[r] = b[r] - b[l - 1]
*/
#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;

int a[N];//输入矩阵 
int b[N];//前缀和矩阵 
int n,m;
int l,r;

int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		b[i]=b[i-1]+a[i];//前缀和的初始化 
	 } 
	 while(m--)
	 {
	 	cin>>l>>r;
	 	cout<<b[r]-b[l-1]<<endl;//输出区间和 
	 }
	return 0;
 } 

AcWing 3956. 截断数组

AcWing 3956. 截断数组

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long LL;
LL ans;
LL cnt;
int n;
int a[N];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		a[i]=a[i-1]+x;//前缀和数组 
	}
	
	for(int i=1;i<=n-2;i++)//枚举的第一个位置 
	{
		if(a[i]==a[n]/3)//第一个刀位置
			cnt++;
		if(a[n]-a[i+1]==a[n]/3)//第二个位置 ---通过枚举第一个位置间接枚举第二个位置
			ans+=cnt;
	}
	if(a[n]%3!=0 || n<3)
		cout<<0<<endl;
	else
		cout<<ans<<endl;
	return 0;
}

AcWing 1230. K倍区间(一维前缀和+同余定理)

AcWing 1230. K倍区间

解析

直接一维前缀和+数学推理
求区间[l,r]的和是k的倍数的个数。
求区间和，我们可以通过前缀和来求出。我们规定sum[i]表示第1个元素到第i个元素的和。

那么sum[r] - sum[l-1]就是区间[l,r]的和。
区间[l,r]的和是k的倍数即(sum[r] - sum[l-1])%k = = 0  即sum[r]%k = = sum[l-1]%k

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;//数据开大点 
const int N = 1e5+10;
int n,k;
LL a[N],b[N];

LL cnt[N];//哈希存储 模相同的区间个数   cnt[x]:余数为x的个数
int main()
{
    cin>>n>>k;
    cnt[0]=1;
    //就是之前找到的是两个 区间的 mod之后相同的值
	//但是对于 mod == 0区间 我可以不用找另外区间，我本身就是符合 mod k == 0 这个条件
	//循环里统计的时候没有考虑这个情况，所以之后要再加上
	for (int i=1;i<=n;i++)
    {
    	cin>>a[i];
        b[i]=b[i-1]+a[i]; //求前缀和
		cnt[b[i]%k]++;// 前缀和取余k的余数的数量  
    }
    
    LL ans=0;//ll数据太大 
    for (int i=0; i<k; i++)//余数必在 0~k-1之间 
    {
       ans+=cnt[i]*(cnt[i]-1)/2; //数学C n 取 2 的公式 
    }
    cout<<ans<<endl;
    return 0;
}

202012-2csp-期末预测之最佳阈值(排序＋一维前缀和)

AcWing 3298. 期末预测之最佳阈值

这道题我主要用到前缀和的算法，首先对数据从小到大进行排序，然后利用前缀和计算出每个数左边有多少个0，进而计算出该数右边有多少个1（包括该数在内），然后让二者相加，即为最后的正确的个数，至于如果有相同的数的话，就只计算出第一个数即可，因为其他的都小于等于第一个数。

从规则来看，我们可以利用前i-1位同学的情况来推断第i位同学的情况。从样例1中可以得到启示
因此考虑使用前缀和算法来进行优化。

注意 ： 遇到相同数时，应只算第一个！！！
为什么呢？
因为这个分界线只能在不同的y之间画，在相同的y之间画的话，i和i−1意义相同，在套公式的时候实际破坏了前缀和，没有发挥前缀和的作用
比如，s[0][i]表示前i个数中0的个数，那如果连续两个y相等，那么计算这个的时候，会多算。本来想算的是第i-1个数前，但是第i-1个数和第i个数是相等的，从而多算了。
在计算s[1][m]−s[1][i−1]也是同理。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef pair<int,int> PII;
#define x first
#define y second
PII a[N];//用pair型数组a记录每个输入的y和result 
int m;
int s[2][N];//s[0][i]---表示前i个数中0的个数               s[1][i]---表示前i个数中1的个数

int main()
{
    cin>>m;
    for(int i=1;i<=m;i++) cin>>a[i].x>>a[i].y;
    sort(a+1,a+m+1);//按第一个键值排序(从小到大) 对数组a按y(安全指数)进行升序排序




    for(int i=0;i<2;i++)
        for(int j=1;j<=m;j++)
            s[i][j]=s[i][j-1]+(i==a[j].y);//两个  一维前缀和 




    int cnt=-1;//匹配项的最大值 
	int res=0;//保存取得最大值时的安全指数
    for(int i=1;i<=m;i++)
    {
        int t=s[0][i-1]+(s[1][m]-s[1][i-1]);//表示每个数作为阈值时预测正确的数量----前i中预测为0 + 前i中预测为1 
        if(t>=cnt) 
        {
            cnt=t;
            res=a[i].x; 
        }
        while(i+1<=m&&a[i].x==a[i+1].x) i++;//遇到相同数时，应只算第一个！！！ ----经典的错误-标准的零分 
    }
    cout<<res<<endl;
    return 0;
}

二维前缀和

AcWing 796. 子矩阵的和

acwing 796. 子矩阵的和

/*
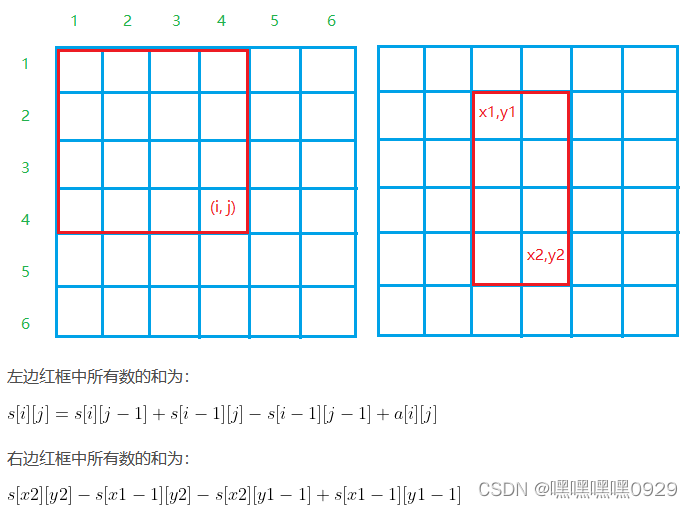
二维前缀和 
b[i, j] = 第i行j列格子左上部分所有元素的和
b[i,j] = b[i-1,j] + b[i,j-1] - b[i-1,j-1] + a[i,j];
以(x1,y1)为左上角，(x2,y2)为右下角的子矩阵的和为：
b[x2,y2] - b[x1-1, y2] - b[x2,y1-1] + b[x1-1, y1-1]
*/

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;

int a[N][N];//输入矩阵 
int b[N][N]; //前缀和矩阵


int main()
{
    int n,m,q;
	cin>>n>>m>>q;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>a[i][j];
			b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+a[i][j];//前缀和数组的初始化 
		}
	}
	while(q--)
	{
	    int x1,x2,y1,y2;
		cin>>x1>>y1>>x2>>y2;
		cout<<b[x2][y2]-b[x1-1][y2]-b[x2][y1-1]+b[x1-1][y1-1]<<endl;//输出子矩阵的和
	}
	return 0;
 } 

AcWing 126. 最大的和

AcWing 126. 最大的和
暴力

#include<iostream>
using namespace std;
const int N=110;
int g[N][N],s[N][N];
int n;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++){
            cin>>g[i][j];
            s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+g[i][j];
        }
    int res=-1e9;
    //枚举一下上下左右四个点---二维前缀和
    for(int x1=1;x1<n;x1++)
        for(int y1=1;y1<n;y1++)
            for(int x2=x1;x2<=n;x2++)
                for(int y2=y1;y2<=n;y2++)
                    res=max(res,s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);
    cout<<res<<endl;
    return 0;
}

AcWing 99. 激光炸弹(二维前缀和+边界处理)

AcWing 99. 激光炸弹
一个数组就行了，在自己身上求前缀和。
xy坐标是从0开始的。

#include<bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 5010;
int n;
int R;
int g[N][N];//原矩阵与前缀和矩阵共用

int main()
{
    cin>>n>>R;
    int x,y,w;
    int l=R,r=R;//因为没有定义地图的长和宽，自己来更新
    for (int i = 0; i < n; i ++ )
    {
        cin>>x>>y>>w;
        x++,y++;//这里是因为习惯上将二维前缀和起始点坐标从(1,1)开始
         l=max(l,x),r=max(r,y);
		 g[x][y]+=w;
    }
    
    for (int i = 1; i <= l; i ++ )
        for (int j = 1; j <= r; j ++ )
                g[i][j]+=g[i-1][j]+g[i][j-1]-g[i-1][j-1];
                
    int res=0;
    for (int i = R; i <= l; i ++ )//至少从左上角的第一个R*R的正方形开始
        for (int j = R; j <= r; j ++ )
            res=max(res,(g[i][j]-g[i-R][j]-g[i][j-R]+g[i-R][j-R]));
    
    cout<<res<<endl;
    return 0;
}

202104-2-csp-邻域均值(二维前缀和+边界处理)

AcWing 3412. 邻域均值

根据题意，需要求一个点附近r范围内矩阵的和，即范围为(2r+1)2大小的矩阵，考虑使用二维前缀和算法

由于矩阵有边界，因此需要对边界范围进行处理：
当要下溢出时，将边界设置为1；当要上溢出时，将边界设置为n

矩阵的大小为(x2-x1+1)*(y2-y1+1)

小细节：如果直接算均值，均值可能为小数，此处可以改写一些判断条件
737

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+10;

int n;
int r;
int t,L;
int matrix[N][N];//输入矩阵
int b[N][N]; //前缀和矩阵 
int main()
{
	cin>>n>>L>>r>>t;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			int x;
			cin>>x;
			b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+x;	//初始化二维前缀和数组 
		}

	int ans=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			//判断矩阵的边界
			int x1=max(i-r,1);
			int y1=max(j-r,1);
			int x2=min(i+r,n);
			int y2=min(j+r,n);
			
			int num=(x2-x1+1)*(y2-y1+1);//统计矩阵中元素的个数
			int sum=b[x2][y2]-b[x1-1][y2]-b[x2][y1-1]+b[x1-1][y1-1];
			if(sum<=num*t)//利用前缀和矩阵    求     矩阵的和
				ans++; 
		}
	cout<<ans<<endl;
	
	return 0;
 } 

差分

深入剖析差分的本质探究差分解法的由来

一维差分

同时改变一个区间中数的大小

AcWing 797. 差分

AcWing 797. 差分
问题：acwing 2041. 干草堆

/*
给区间[l, r]中的每个数加上c：B[l] + c, B[r + 1] - c
差分可以看成前缀和的逆运算
*/

/*
首先给定一个原数组a：a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b ： b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。
换句话说，每一个a[i]都是b数组中从头开始的一段区间和。
*/
#include<iostream>
using namespace std;
const int N=100010;

int n,m;
int a[N],b[N];//a数组是b数组的前缀和数组 

int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		b[i]=a[i]-a[i-1];//构建差分数组 
	}
	while(m--)
	{
		int l,r,c;
		cin>>l>>r>>c;
		b[l]=b[l]+c,b[r+1]=b[r+1]-c; //将序列中[l, r]之间的每个数都加上c
	}	 
	for(int i=1;i<=n;i++)
		a[i]=a[i-1]+b[i];//前缀和运算
	for(int i=1;i<=n;i++)
		cout<<a[i]<<" ";//输出最终序列 
	return 0;
 } 

AcWing 3729. 改变数组元素

AcWing 3729. 改变数组元素

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;

int b[N];//差分数组

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		int n;
		cin>>n;
		for(int i=0;i<=n;i++) b[i]=0;//因为差分数组要使用多次，每次使用前初始化
		
		for(int i=1;i<=n;i++)
		{
			int x,l,r;
			cin>>x;
			l=max(1,i-x+1);//差分数组的左端 
			r=i;//差分数组的右端 
			b[l]+=1;
			b[r+1]-=1;
		 }
		 for(int i=1;i<=n;i++)
		 {
		 	b[i]=b[i]+b[i-1];
		 	cout<<!!b[i]<<" ";
		 }
		cout<<endl;
	 } 
	return 0;
 } 

202203-2csp-出行计划

AcWing 4455. 出行计划

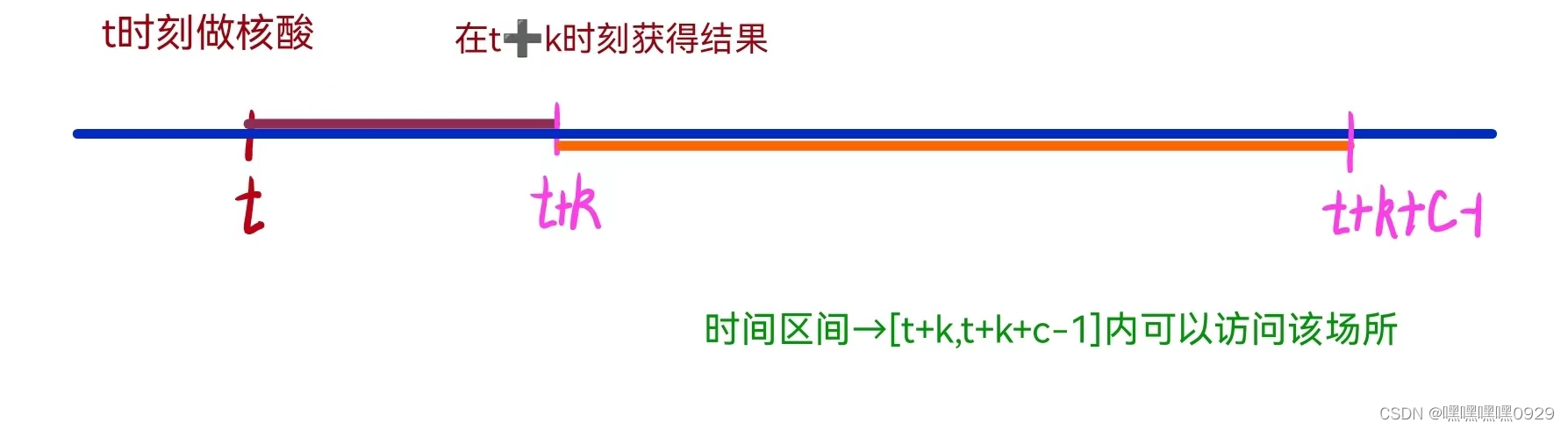
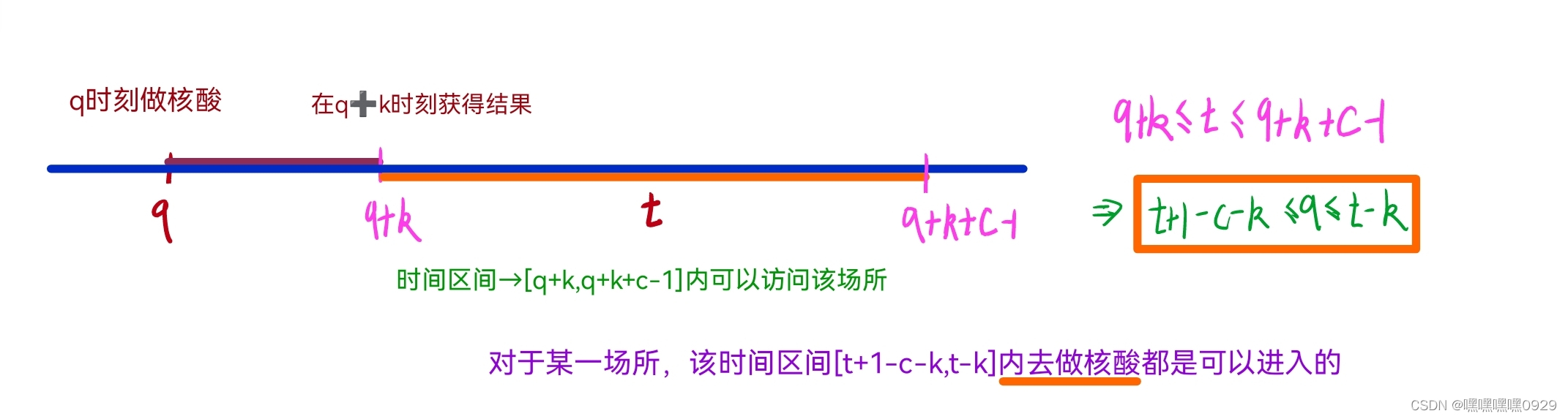符合题意的做核酸区间+1----->差分来做

满分写法

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;

int n;
int m;
int k;
int res[N]={0};//差分数组 
int main()
{
	cin>>n>>m>>k;
	for(int i=0;i<n;i++) //判断出进入该场所需要的最早时间核酸报告（left）和最晚时间核酸报告（right） 
	{
		int t;//t时刻进入场所
		int c;//场所维持时间
		cin>>t>>c;
		int l,r;
		l=max(t-k-c+1,0);
		r=max(t-k,0);
		res[l]+=1, res[r+1]-=1;//表示处于这个时间段内，场所是可以访问的 			
	}
	for(int i=1;i<=N;i++)//一维前缀和 
	{
		res[i]=res[i-1]+res[i];
	}
	for(int i=0;i<m;i++)//输出查询 
	{
		int q;
		cin>>q;
		cout<<res[q]<<endl;	
	}	
	
	return 0;
}

AcWing 100. 增减序列

AcWing 100. 增减序列
AcWing 100. 疑难点详解，看完不会你来打我

//要使最后的数都一样，那么b数组中的b2=>bn  一定全 0

//贪心的思想，来使得b中所有数变成零
//我们知道我们在做b[L]++,b[R+1]--;操作的时候，要找两个数配对，那么 负数++，正数--，是不是就最快了。
// 但是最终结果可能依然不是全 0 的，因为 abs(sum(正数))可能！=abs(sum(负数))
//所以，我们可以 让最后不等于0 的数全和 b1||bn+1来换。


/*
那么题目就变成了对一个数组可进行三种操作
1对两个元素一个加一一个减一
2对一个元素加一
3对一个元素减一
*/        //后面两种操作实质是对一个元素和队首或队尾进行操作


/*最终的序列有 abs(pos-neg)+1种
因为还剩下的abs(pos-neg) 种操作是对队尾或队首的操作
队尾或队首就会影响这个数列的值，所以最多加那么多次，最少一种
*/
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef long long LL;
int n;
int a[N];
int b[N];
LL pos,neg;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		b[i]=a[i]-a[i-1];//差分数组的初始化 
	}
	for(int i=2;i<=n;i++)
	{
		if(b[i]>0)
			pos+=b[i];//差分数组第二个元素起所有正数和 
		else
			neg-=b[i];//差分数组第二个元素起所有负数和的绝对值 
	}
	cout<<min(pos,neg)+abs(pos-neg)<<endl;
	cout<<abs(pos-neg)+1<<endl; 
	
	
	return 0;
 } 

AcWing 101. 最高的牛(差分+区间处理)

AcWing 101. 最高的牛

题目中说对于两头牛它们可以互相看见，说明两牛之间的牛的身高都比这两只低
因此根据最优的原则，我们可知中间的牛可以都比这两只小1即可 。

现在我们考虑关系会不会有交叉的情况。
假设i<j<k<l;存在关系ik和jl
因为存在关系ik，因此k的身高大于j，又因为存在jl，所以j的身高大于k
前后互相矛盾，因此不存在关系存在交叉的情况。

所以对于该问题，我们可以假设全部都是最高身高
然后每出现一对关系，就将他们之间的牛的身高全减1
因为涉及区间加减1，我们可以采用差分和前缀和的关系来解决该问题
具体实现看代码，注意关系判重。

#include<bits/stdc++.h>
using namespace std;
const int N=5e3+10;

int height[N];//差分数组 
set<pair<int,int>> S; 
int main()
{
	int N,P,H,M;
	cin>>N>>P>>H>>M;
	height[1]=H;//直接初始化差分数组
	for(int i=0;i<M;i++)
	{
		int A,B;
		cin>>A>>B;
		if(A>B) swap(A,B);//调整顺序 
		if(!S.count({A,B}))//去重 
		{
			S.insert({A,B});
			height[A+1]--;//A-----B之间的所有牛身高-- 
			height[B]++;
		} 
	
	}
		for(int i=1;i<=N;i++)//求差分数组的一维前缀和 
		{
			height[i]+=height[i-1];
			cout<<height[i]<<endl;
		}
	
	return 0;
}

水位每上涨一个高度差后对数组中数的关系有怎样的影响

202109-2-csp-非零段划分

AcWing 4007. 非零段划分

区间原地划分时可以观察相邻元素之间的大小关系是否与划分有关。
前缀和与差分实现单位时间内区间数值整体加1。
 当a[i]>a[i-1]时，只要p取到区间a[i-1]到a[i]-1中的值，都能构成一个新的非零段。这就是p与数组的关系
 根据这个关系利用前缀和与差分实现单位时间内区间数值整体加1，将双重循环改进至单层，降低计算时间。

再回看这里，这里干了个什么事呢？
就是 如果a[i]>a[i-1]，也就是后一个数比前一个大
那么，当p取到它们中间的值时，就会出现一个非零段；
而当p比 a[i]大的时候，就会都变成0，没有非零段；

例如(a[1]=3) >(a[0]=0) 
当p取0、1、2时都会出现一个非零段，但当p取3时，就都变成0，没有非零段
b[0] = 1 b[3] = -1
b[0]从0变为1，为什么？
p=0的时候，有1个非零段，同理p=1、2 、3也只有一个非零段，只用对b[0]加1就行了
为什么只加一个1呢？
因为差分数组只需要改变一个值，就可以影响一个区间的值
为什么又要把b[3]从0变为-1呢?
因为p>3的时候，3也变成0了，没有非零段了

实际上就是从1到n持续循环这个过程，按数组a的元素的值，为差分数组b的下标
最后再对差分的原数组(进行前缀和操作)进行最大值求和；

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
const int M=1e4+10;

int n;
int a[N];
int b[M];//差分数组 
int main()
{
	cin>>n;
	
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		if(a[i-1]<a[i])//a[i-1]到a[i]-1段的p都能构成新的非零段
		{
			b[a[i-1]]++;//处理差分数组以实现区间整体+1
			b[a[i]]--; 
		}		
	}
	int ans=0;//返回取值最大的p 

	for(int i=1;i<=M;i++)//差分数组  求  一维前缀和
	{
		b[i]+=b[i-1];
		if(b[i]>ans) ans=b[i];
	 } 
	cout<<ans<<endl;
	
	return 0;
}

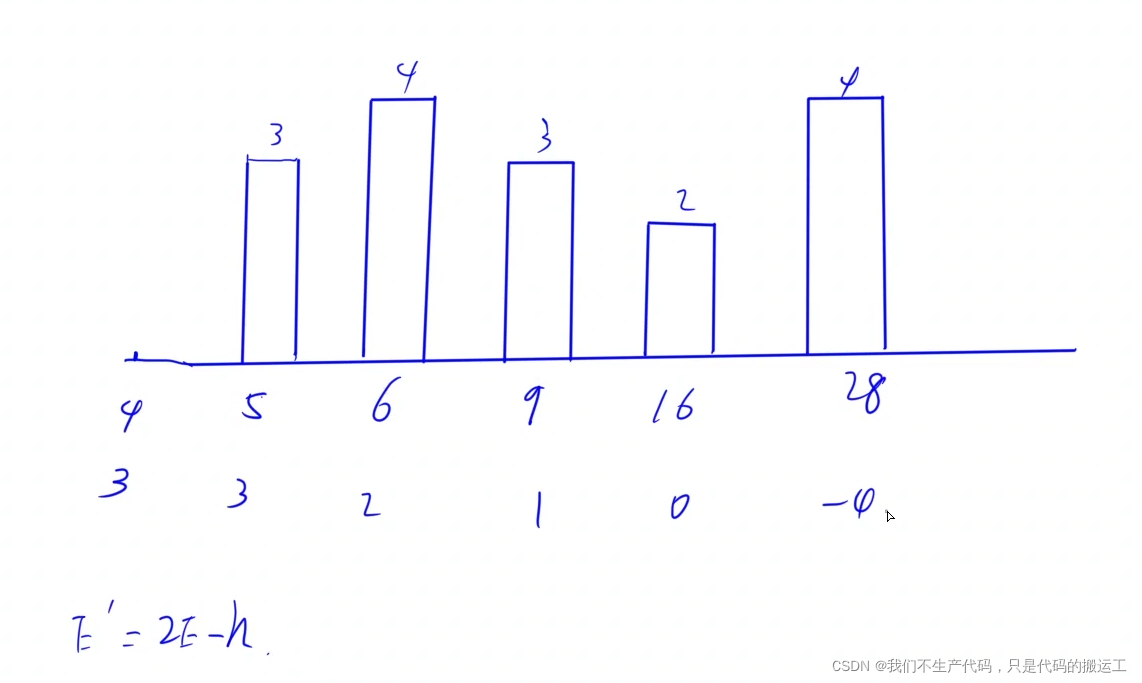
利用---海平面下降--海岛个数的思想去理解这个题目
AcWing 2014. 岛问题的变形
AcWing 2014. 岛---海平面一直上升
AcWing 4007. 非零段划分---海平面一直下降

#include<bits/stdc++.h> 
using namespace std;
const int N = 500010, M = 10010;

int n;
int a[N];//山峰的高度 

//海水退却到i时，会比高度为i+1时，多出来的山峰个数 
int cnt[M];//所有高度为i的山峰的贡献
int main()
{
    cin>>n;
    a[0]=a[n+1]=0;//为了左右两边判断方便 
    for(int i=1;i<=n;i++) cin>>a[i];
    n=unique(a+1,a+n+1)-a-1;//判重---所有连续高度相同的山峰可以看做为一个 
 

    for(int i=1;i<=n;i++)
    {
        int x=a[i-1];
		int y=a[i];//处理y高度山峰的贡献 
		int z=a[i+1];
        if (x<y && z<y) cnt[y]++;//---海平面下降---山峰个数新增加一个 
        else if(x>y && z>y) cnt[y]--;//---海平面下降---山峰会被减少一个
		 
        //这里少了两种情况---x<y<z//x>y>z---这两种---在海平面下降的情况下山峰的个数不会发生变化 
    }

    int res=0;	//定义答案 
	int sum=0;	//定义当前山峰漏出来的段数 
    for (int i=M-1;i;i--)//随着海平面的下降---山峰的增加个数 ----起初没有山峰(全在海平面以下) 
    {
        sum+=cnt[i];
        res=max(res,sum);
    }

    cout<<res<<endl;
    return 0;
}

AcWing 2014. 岛(贪心＋模拟)

AcWing 2014. 岛(离散化+差分)c++最短代码，同非零段划分(含对差分算法的深入探究)
贪心＋模拟

#include<bits/stdc++.h>
#include <iostream>
#include <cstring>
#include <algorithm>

#define x first
#define y second 
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;

int n;
int h[N];
PII q[N];

int main()
{
    cin>>n; 
    for (int i=1; i<=n;i++)	cin>>h[i];

    n=unique(h+1,h+n+1)-h-1;  // 判重----删掉相邻的重复元素 
    h[n+1]=0;  // 后续代码可能会用到第n + 1个位置，需要把第n + 1个位置清空

    for (int i=1; i<=n;i++) q[i] = {h[i],i};
    sort(q+1,q+n+1);//按高度排序 

    int ans = 0; 
	int cnt = 1;//初始时岛屿数量----没有水的时候 
    for (int i = 1; i <= n; i ++ )
    {
        int k=q[i].y;//当前海平面长到k高度 
        if (h[k-1]<h[k] && h[k+1]<h[k]) cnt -- ;//比两边都大 
        else if (h[k-1]>h[k] && h[k+1]>h[k]) cnt ++ ;//比两边都矮时 

        if (q[i].x != q[i + 1].x)//按高度排序（失散多年的兄弟），当高度不一样时跟新ans 
            ans = max(ans, cnt);
    }
    cout<<ans<<endl;

    return 0;
}

差分写法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>


typedef long long LL;

using namespace std;
const int N = 100005,M = 1e9+1;
int a[N];
map<int ,int >b;
int n;
int main()
{
    cin >> n;

    for (int i = 1; i <= n; i ++ ){
        cin >> a[i];
        if(a[i]>a[i-1]){
            //数的大小在[a[i-1],a[i]-1]之间的所有数大小都+1
            b[a[i-1]]++,b[a[i]]--;
        }
    }
    LL sum = 0 ,res = 0;
    for (auto i:b ){
        //求前缀和
        sum+=i.second;
        res = max(res,sum);
    }
    cout << res;
}

二维差分

AcWing 798. 差分矩阵(二维差分)

798. 差分矩阵
【c++详细题解】

/*
给以(x1,y1)为左上角，(x2,y2)为右下角的子矩阵中的所有元素加上c：
S[x1,y1]+=c, S[x2 +1,y1]-=c, S[x1,y2+1]-=c, S[x2+1,y2+1]+=c
*/

#include <iostream>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];//输入矩阵 
int b[N][N];//b是差分矩阵 
int n, m, q;

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    cin>>n>>m>>q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            insert(i, j, i, j, a[i][j]);      //始化构造差分数组
  
    // 多次进行矩阵区域插入
    while (q--)
    {
        int x1, y1, x2, y2, c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1, y1, x2, y2, c);
    }   
    // 对差分矩阵求二维前缀和
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            cout<<b[i][j]<<" ";
        }
    	cout<<endl; 
    }
    
    return 0;
}

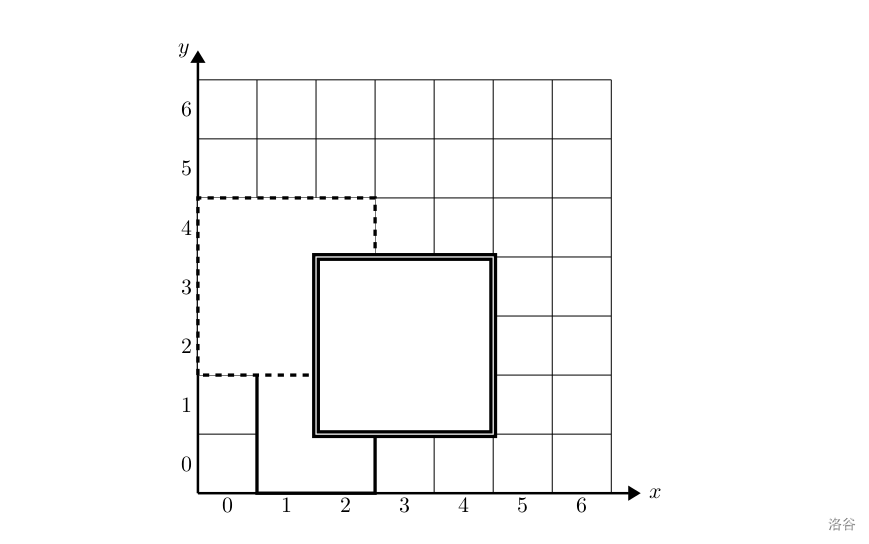
201409-2-csp-画图—二维差分

AcWing 3203. 画图

每个格子的编号---是它的左下角坐标---从[i][j]开始

暴力做法

#include<bits/stdc++.h>
using namespace std;
const int N=110;

bool st[N][N];//标记[i][j]格子是否被涂色---每个格子的坐标---是它左下角的坐标 

int main()
{
	int n;
	cin>>n;
	while(n--)
	{
		int x1,x2,y1,y2;
		cin>>x1>>y1>>x2>>y2;
		for(int i=x1;i<x2;i++)//每个格子的坐标---是它左下角的坐标 
		{
			for(int j=y1;j<y2;j++)
			{
				st[i][j]=true;
			}
		}
	}
	
	int ans=0;
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<N;j++)
		{
			if(st[i][j])//将涂色的格子统计个数 
				ans++;
		}
	}
	cout<<ans<<endl; 
	return 0;
}

每个格子的坐标---是它右上角坐标---二维差分方便---从[1][1]开始

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int b[N][N];

int ans;
void insert(int x1, int y1, int x2, int y2, int c)//二维差分模板 
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main()
{
	int n;
	cin>>n;
	
	while(n--)
	{
		int x1,x2,y1,y2;
		cin>>x1>>y1>>x2>>y2;
		insert(x1+1,y1+1,x2,y2,1); //坐标从 [i][j]开始---方便---二维差分 
		
	}
	for(int i=1;i<N;i++)
	{
		for(int j=1;j<N;j++)
		{
			b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1]; //二维前缀和 
			if(b[i][j])	ans++;
		}
	}
	cout<<ans<<endl;
	return 0;
}

快速排序

双指针算法

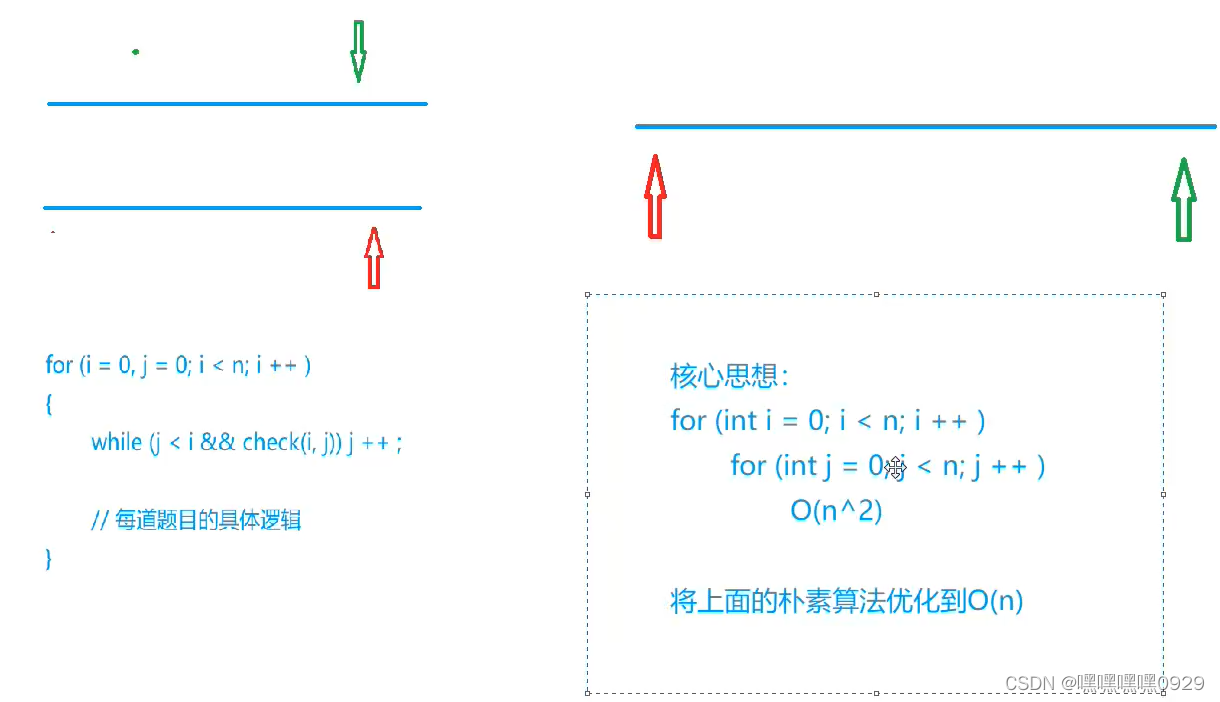
算法模型---思路：先找出暴力解法，根据题目性质，优化到双指针

1.对撞指针------左右两个指针，向中间靠拢。

2.快慢指针------左右两个指针，一快一慢

3.滑动窗口

4.归并排序---操作两个数组

AcWing 799. 最长连续不重复子序列—滑动窗口

AcWing 799. 最长连续不重复子序列

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];
int s[N];
int main()
{
	int n;
	cin>>n;
	int ans=0;//答案 
	for(int i=0;i<n;i++) cin>>a[i];
	//[l,r]区间端点 ----双指针维护的是以a[r]为结尾的最长不重复子序列，长度为r-l+1
	for(int r=0,l=0;r<n;r++) 
	{
		s[a[r]]++;//存储子序列中a[r]出现的次数 
		while(l<r && s[a[r]]>1)   //当a[r]重复时，先把a[l]次数减1，再右移l
		{
			s[a[l]]--;
			l++;//区间左端点----向右移动 
		}
		ans=max(ans,r-l+1); //更新最大长度 
	}
	cout<<ans<<endl;
	return 0;
 } 

AcWing 3768. 字符串删减—滑动窗口

AcWing 3768. 字符串删减

#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;
string s;
int ans;
int main()
{
	int n;
	cin>>n;
	cin>>s;
	for(int l=0;l<n;l++)//左指针右移----[l,r] 
	{
		if(s[l]=='x')//如果s[l]不是'x'时，继续往右移动----直到枚举到第一个'x' 
		{
			int r=l+1;//右指针设置 
			while(r<n && s[r]=='x')	r++;//右指针右移 
			ans+=max(0,r-l-2);//答案+这个区间需要删除的'x'的数量 
			l=r-1;//重新设置左指针 
		}
	}
	cout<<ans<<endl;
	return 0;
 } 

AcWing 1238. 日志统计—滑动窗口

蓝桥杯2018年第九届真题-日志统计

排序+双指针 
对所有的赞按照时间从小到大排序
通过双指针i,j维护长度不大于d的区间，并记录该区间的中所有帖子获得的赞数

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
typedef pair<int, int> PII;
PII q[N];//用于存储日志ts, id
#define ts first
#define id second
int n,d,k;//n行，d时间间隔，k个赞
int ts,id;
int cnt[N];//用来存储每个id当前获得的点赞数
bool st[N];用于存储每个帖子是否是热帖

int main()
{
    cin>>n>>d>>k;
    for (int i=0;i<n;i++) cin>>q[i].ts>>q[i].id;
    sort(q,q+n);//按时间排序 

    for (int r=0,l=0;r<n;r++)//双指针算法，[l,r]
    {
        cnt[q[r].id]++;//当前第r个记录顺序的id的点赞数++;
        
        
        while(q[r].ts-q[l].ts>=d)//如果俩个帖子时间相差超过d------说明该赞无效
        {
            cnt[q[l].id]--;//获赞的时间太久远了，赞作废
            l++;//要把指针l右移
        }
        if(cnt[q[r].id]>=k)//如果该id贴赞超过k，说明是热帖
            st[q[r].id]=true;
            
    }
    
    for(int i=0;i<N;i++)//最多有1e5个id
        if(st[i])
            cout<<i<<endl;
    return 0;
    
}

AcWing 800. 数组元素的目标和—对撞指针—操作两个数组

AcWing 800. 数组元素的目标和

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];
int b[N];
int main()
{
	int n,m,x;
	cin>>n>>m>>x;
	for(int i=0;i<n;i++) cin>>a[i];
	for(int i=0;i<m;i++) cin>>b[i];
	
	
	for(int l=0,r=m-1;l<n;l++)//对撞指针---l左指针  r右指针 
	{
		while(r>=0 && a[l]+b[r]>x) r--;//右指针左移 
		
		if(r>=0 && a[l]+b[r]==x)//符合答案，输出 
			{
				cout<<l<<" "<<r<<endl;
				break;
			}
	}
	return 0;
}

AcWing 2816. 判断子序列—操作两个数组

AcWing 2816. 判断子序列
题解

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;

int a[N];
int b[N];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=0;i<n;i++) cin>>a[i];
	for(int i=0;i<m;i++) cin>>b[i];
	
	int l=0;//第一个数组的指针 
	for(int r=0;r<m;r++)//第二个数组的指针移动 
	{
		if(l<n && a[l]==b[r])	l++;//第一个数组的指针移动 
	}
	if(l==n)
		cout<<"Yes"<<endl;
	else
		cout<<"No"<<endl;
	return 0;
}

AcWing1532. 找硬币—对撞指针

acwing1532. 找硬币

双指针要求具有单调性

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	sort(a+1,a+n+1);
	int l=1,r=n;
	int suit_l=0,suit_r=0;
	while(l<r)//指针未相遇就一直执行
	{
		//下面的if 不能调动顺序-------经典错误，标准零分
		//如果调动顺序-----2,3,1时，假如2/3不满足，会修改l/r的值，使得到达1的时候，l/r变动 
		if(a[l]+a[r]==m)//-----1 
			{
				suit_l=a[l];
				suit_r=a[r];
				break;
			}
		if(a[l]+a[r]>m)//------2
			r--;
		if(a[l]+a[r]<m)//------3
			l++;
		
	}
	if(suit_l+suit_r==m)
		cout<<suit_l<<" "<<suit_r<<endl;
	else
		cout<<"No Solution"<<endl;
	return 0;
}

AcWing1574.接雨水—对撞指针

acwing1574. 接雨水

双指针，从左和右出发两个指针，每次记录左右两侧最大值
l_max为[1,l]最大值，r_max为[r,n]最大值
每次从最大值小的那一方开始收水
比如l_max < r_max,可以收左边的水，因为l左侧[1,l]最大值确定，右侧[l,n]有值大于左侧最大值,反之亦然。
一列一列收水，一次收完一列水

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N];

int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)	
		cin>>a[i];
	int l=1,r=n;
	int maxl=0,maxr=0;
	int ans=0;//保存的返回值--接到的雨水数量 
	while(l<r)
	{
		maxl=max(maxl,a[l]);//更新左边最大值-----当前l的左边最高值 
		
		maxr=max(maxr,a[r]);//更新右边最大值-----当前r的右边最高值 
		
		if(maxl<maxr)
		{
			ans+=maxl-a[l];
			l++;//左指针---右移 
		 }
		else
		{
			ans+=maxr-a[r];
			r--;//右指针---左移 
		 } 
		
	}
	cout<<ans<<endl; 
	return 0;
 } 

位运算

离散化

第二讲 数据结构

集合

AcWing 3542. 查找

AcWing 3542. 查找

#include<bits/stdc++.h>
using namespace std;

int main()
{
	int n,m;
	unordered_set<int> S;//定义一个集合存储a数组中的元素 
	cin>>n;
	while(n--)
	{
		int x;
		cin>>x;
		S.insert(x);
	 } 
	 
	 
	cin>>m;
	while(m--)
	{
		int x;
		cin>>x;
		if(S.count(x))
			cout<<"YES"<<endl;
		else
			cout<<"NO"<<endl;
	}
	return 0; 
 } 

单链表

双链表

栈(stack)

stack是一种先进后出(First In Last Out,FILO)的数据结构
只有stack顶端的元素，才有机会被外界取用。Stack不提供遍历功能





数据存取操作
push(elem);//向栈顶添加元素
pop();//从栈顶移除第一个元素
top();//返回栈顶元素




大小操作
empty();//判断堆栈是否为空
size();//返回堆栈的大小

AcWing 3302. 中缀表达式求值—向零取整

#include<bits/stdc++.h>
using namespace std;
unordered_map<char,int> pr;//保存运算符优先级
stack<int> num;//运算数栈 
stack<char> op;//运算符栈 

void eval()//执行某种运算 
{
	int x;
	
	auto b=num.top();num.pop();
	auto a=num.top();num.pop();
	auto c=op.top();op.pop();
	
	if(c=='+') x=a+b;
	else if(c=='-') x=a-b;
	else if(c=='*') x=a*b;
	else x=a/b;
	num.push(x);
}

int main() 
{
	pr['-']=1;//初始化运算符的优先级 
	pr['+']=1;
	pr['*']=2;
	pr['/']=2;
	string s;
	cin>>s;
	for(int i=0;i<s.size();i++)
	{
		if (isdigit(s[i]))//如果是运算数时 
        {
            int j = i, x = 0;
            while (j < s.size() && isdigit(s[j]))
                x = x * 10 + s[j ++ ] - '0';
            num.push(x);
            i = j - 1;
        }
		else if(s[i]=='(')//左括号---直接入栈 
			op.push(s[i]); 
		else if(s[i]==')')//右括号---操作到左括号为止
		{
			while(op.top()!='(')
				eval();
			op.pop();//左括号出栈 
		 }
		else//当是运算符时 
		{
			while(op.size() && op.top()!='(' && pr[op.top()]>=pr[s[i]]) eval();
			op.push(s[i]);
		 } 
	}
	
	while(op.size())
		eval();
	cout<<num.top()<<endl;
	return 0;
}

201903-2-csp-二十四点—向下取整

AcWing 3273. 二十四点

#include<bits/stdc++.h>
using namespace std;
stack<int> num;
stack<char> op;
unordered_map<char,int> pr;
int n;

void eval()
{
	auto b=num.top();num.pop();
	auto a=num.top();num.pop();
	auto c=op.top();op.pop();
	int x;
	if(c=='+')
		x=a+b;
	else if(c=='-')
		x=a-b;
	else if(c=='x')
		x=a*b;
	else//向下取整---除法 
	{
		if(a*b>=0)//当ab同号时 
			x=a/b;
		else
		{
			if(a%b==0)
				x=a/b;
			else
				x=a/b-1;//c++默认除法---向零取整---题干要求---向下取整 
		} 
	}
	num.push(x); 
 } 
int main()
{
	pr['+']=pr['-']=1;
	pr['x']=pr['/']=2;//整除---向下取整---c++默认是向零取整 
	cin>>n;
	while(n--)
	{
		//清空栈的操作 
		num = stack<int>();
        op = stack<char>();
		string s;
		cin>>s;
		for(int i=0;i<s.size();i++)
		{
			if(s[i]>='0' && s[i]<='9')		//如果是运算数时 
				num.push(s[i]-'0');
			else 		//如果是运算符时 
			{
				while(op.size() && pr[op.top()]>=pr[s[i]])	eval();
				op.push(s[i]); 
			}
		 }
		while(op.size())	eval();
		if(num.top()==24)
			cout<<"Yes"<<endl;
		else
			cout<<"No"<<endl; 
		 
	}
	return 0;
}

中缀表达式转后缀表达式—AcWing 3302. 中缀表达式求值—改编题目

是由上面的中缀表达式求值---去掉运算数栈----遇到运算数直接输出

#include<bits/stdc++.h>
using namespace std;
unordered_map<char,int> pr;//保存运算符优先级

stack<char> op;//运算符栈 

void eval()//执行某种运算 
{
	int x;
	
	auto c=op.top();op.pop();
	cout<<c<<" ";
}

int main() 
{
	pr['-']=1;//初始化运算符的优先级 
	pr['+']=1;
	pr['*']=2;
	pr['/']=2;
	string s;
	cin>>s;
	for(int i=0;i<s.size();i++)
	{
		if (isdigit(s[i]))//如果是运算数时 
        {
            int j = i, x = 0;
            while (j < s.size() && isdigit(s[j]))
                x = x * 10 + s[j ++ ] - '0';
            cout<<x<<" "; 
            i = j - 1;
        }
		else if(s[i]=='(')//左括号---直接入栈 
			op.push(s[i]); 
		else if(s[i]==')')//右括号---操作到左括号为止
		{
			while(op.top()!='(')
				eval();
			op.pop();//左括号出栈 
		 }
		else//当是运算符时 
		{
			while(op.size() && op.top()!='(' && pr[op.top()]>=pr[s[i]]) eval();
			op.push(s[i]);
		 } 
	}
	
	while(op.size())
		eval();
	return 0;
}

队列(queue/deque/priority_queue)

Queue——单端队列

Queue是一种先进先出(First In First Out,FIFO)的数据结构-------常见队列
只有queue的顶端元素，才有机会被外界取用-------------Queue不提供遍历功能
 qeque<int> q;




queue存取、插入和删除操作
q.push(elem);//往队尾添加元素
auto t=q.pop();//从队头移除第一个元素
auto t=q.back();//返回最后一个元素
auto t=q.front();//返回第一个元素





queue大小操作
empty();//判断队列是否为空
size();//返回队列的大小

Deque——双端队列

dueque 可以在头尾两端分别做元素的插入和删除操作
deque<int> dq;



deque双端插入和删除操作
push_back(elem);//在容器尾部添加一个数据
push_front(elem);//在容器头部插入一个数据
pop_back();//删除容器最后一个数据
pop_front();//删除容器第一个数据

优先队列—堆

priority_queue//优先队列-----队列和排序的完美结合体
元素被赋予优先级，当访问元素时，具有最高级优先级的元素先被访问



默认操作
q.empty()          //如果队列为空，则返回true，否则返回false
q.size()              //返回队列中元素的个数
q.pop()              //删除队首元素，但不返回其值
q.top()               //返回具有最高优先级的元素值，但不删除该元素
q.push(item)      //在基于优先级的适当位置插入新元素

大顶堆构造一个空的优先队列（此优先队列默认为大顶堆）
priority_queue<int,vector<int>,less<int>> big_heap;

小根堆构造一个空的优先队列,此优先队列是一个小顶堆
priority_queue<int,vector<int>,greater<int>>small_heap;

201712-2csp游戏(queue)—约瑟夫问题

AcWing 3253. 游戏

#include<bits/stdc++.h>
using namespace std;
queue<int> q;

int n,k;
bool check(int x)
{
	if(x%k==0||x%10==k)
		return true;
	else
		return false;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
		q.push(i);
	int count=1;// 从1开始报数
	while(q.size()>1)
	{
		int t= q.front();
		q.pop();
		if(!check(count))// 如果这个数不用出局，那就再加到队尾
			q.push(t);
		count++;
	}
	cout<<q.front()<<endl;
	return 0;
 } 

单调栈

单调队列

KMP

Trie

并查集

并查集思想（重点)
我们可以把每个连通分量看成一个集合，该集合包含了连通分量的所有点。而具体的连通方式无关紧要，好比集合中的元素没有先后顺序之分，只有“属于”与“不属于”的区别。图的所有连通分量可以用若干个不相交集合来表示。
分为三部分：
（1）初始化：使每个结点的初始根节点为自己，并且每个结点构成一颗树，树的深度是1；
（2）查找：使用递归来查找每个结点的父亲结点；
（3）合并：将不同父节点的结点合并；
注：这里的并查集是优化后的，即：进行了路径压缩。如果题目中无要求，可以只写简单的并查集算法

AcWing 837. 连通块中点的数量

AcWing 837. 连通块中点的数量

3

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;

int n,m;
int p[N];//存储i的父亲结点的编号
int cnt[N];//记录---i所在树中结点的个数
 
int find(int x)//返回x的祖宗结点+路径压缩 
{
	if(x!=p[x])//x不是根节点时 
		p[x]=find(p[x]); //认祖为父 
	return p[x];//返回x的祖宗结点	
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		p[i]=i;
		cnt[i]=1; 
	}
		
	while(m--)
	{
		string op;
		int a,b;
		cin>>op>>a;
		if(op=="C")
		{
			cin>>b;
			int aa=find(a);
			int bb=find(b);
			if(aa!=bb)
			{
				p[aa]=bb;
				cnt[bb]+=cnt[aa];
			}			
		}
			
		else if(op=="Q1")
		{
			cin>>b;
			if(find(a)==find(b))
				cout<<"Yes"<<endl;
			else
				cout<<"No"<<endl;
		 }
		 else 
		 {
		 	cout<<cnt[find(a)]<<endl;
		  } 
	 } 
	return 0;
}

堆

哈希表(map/unordered_map)

map<key,value> m--------Map所有的元素都是pair---------map内部的所有元素都是有序的
第一个可以称为关键字(key)，每个关键字只能在map中出现一次；第二个可能称为该关键字的值(value)；
first                                    			second






map插入数据元素操作
//1通过pair的方式插入对象
m.insert(pair<int, string>(3, "小张"));
m.inset(make_pair(-1, "校长"));
//2通过数组的方式插入值--------可以覆盖以前该关键字对应的值
mapStu[3] = "小刘";
mapStu[5] = "小王";





map查找操作
方法一：[]
map<int, int> mp;
cout << mp[1] << endl;

count(key)         返回指定key出现的次数
-------如果有，返回1；否则，返回0。注意，map中不存在相同元素，所以返回值只能是1或0






map大小操作
size();//返回容器中<key,value>的个数





遍历操作
for(auto &t : m)
    cout<<"key:"<<t.first<<" value:"<<t.second<<endl;
 

unordered_map--------其元素的排列顺序是杂乱的，无序的

201412-1csp门禁系统(map)

    采用map存储数据，key存储编号，value存储次数
    边输入边输出，先m[x]++，再输出m[x]

#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;

const int N=1e3+10;

unordered_map<int,int>m;
int n;
int main()
{
	cin>>n;
	int temp;
	for(int i=0;i<n;i++)
	{
		cin>>temp;
		m[temp]++;
		cout<<m[temp]<<" ";
	}
	return 0;
 } 

201409-1csp相邻数对(map)

AcWing 3202. 相邻数对

    为了便于直接寻找相差1的数，我们采用map结构
    map用来判断是否存在相应的值，如果存在则为1，不存在为0
    用vector存储整个数值，然后对每个数值进行单独判断

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+10;

int n;
vector<int> v;//数组用来存储数据遍历一遍
unordered_map<int,int> m;//用哈希表来判断该点是否存在
int ans=0;//返回答案 
int main()
{
	cin>>n;
	for(int i=0;i<n;i++)
	{
		int x;
		cin>>x;
		v.push_back(x);//用数组存储下来 
		m[x]=1; //存在该点 
	}
	for(auto i: v)
	{
		if(m[i-1]!=0)
		{
			m[i-1]=0;
			ans++;
		}
	 }
	 cout<<ans<<endl;
	 return 0; 
 } 

201312-1csp出现次数最多的数(map)

#include<bits/stdc++.h>
using namespace std;
const int N= 1e4+10;
map<int,int> m;

int n;
int main()
{
	cin>>n;
	for(int i=0;i<n;i++)
	{
		int index;
		cin>>index;
		m[index]++;
	}
	
	int max=0,index=0;
	for(auto x:m)
	{
		if(x.second>max)
		{
			index=x.first;
			max=x.second;
		}
	 } 
	 cout<<index<<endl;
	return 0;
}

202006-2csp稀疏向量(map)

map用于存储稀疏数据是最有效的，也可以用来存储稀疏向量。

2个向量不必都存储，能够边读入数据边计算可以节省存储，也有助于提高计算速度。

先读入数据存储在数据结构中，再进行处理是倒腾，既浪费存储又浪费时间，完全没有必要。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
map<int,int> M;
LL n,a,b;
LL ans=0;
int main()
{
	cin>>n>>a>>b;
	int index,val;
	for(int i=0;i<a;i++)
	{
		cin>>index>>val;
		M[index]=val;
	}
	for(int i=0;i<b;i++)
	{
		cin>>index>>val;
		ans+=val*M[index];//这里利用了map的性质，快速查找到了index(key)对应的value
	}
	cout<<ans<<endl;
	
	return 0;
 } 

AcWing.3447. 子串计算

3447. 子串计算

#include<bits/stdc++.h>
using namespace std;
const int N =110;

int main()
{
	string str;
	while(cin>>str)
	{
		map<string,int> hash;//map天然字典序---排序 
	
		for(int r=0;r<str.size();r++)//枚举一下右边端点 
			for(int l=0;l<=r;l++)//枚举一下左边端点 			
				hash[str.substr(l,r-l+1)]++;//substr：第一个参数：起始下标，第二个参数：截取字符串的长度(r-l+1) 
	
		for(auto &t:hash)
			if(t.second>1)
				cout<<t.first<<" "<<t.second<<endl;	
	}
	return 0;
 } 

AcWing 3581. 单词识别

AcWing 3581. 单词识别

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;

int main()
{
	string str;
	getline(cin,str);
	map<string,int> hash;
	
	for(int i=0;i<str.size();i++)
	{
		int j=i;
		string word;
		if(isalpha(str[j]))//如果遇到的是字母时
		{
			while(j<str.size() && isalpha(str[j]))
				word+=tolower(str[j++]);//将小写字母-->大写字母的函数---toupper()
			i=j;//跳出上次循环时---j指向的是非字母
			hash[word]++; 
		}
			
	}
	
	for(auto &t:hash)
	{
		cout<<t.first<<":"<<t.second<<endl; 
	}
	return 0;
}

第三讲 搜索与图论

leetcode

leetcode.200岛屿数量(bfs/dfs)

leetcode.200岛屿数量(bfs dfs)

leetcode.130被围绕的区域(dfs,bfs)

leetcode.130被围绕的区域(dfs,bfs)

leetcode.547省份数量(dfs,bfs)

leetcode.547省份数量(dfs,bfs)

Flood fill算法—洪水覆盖算法

AcWing1113. 红与黑

acwing1113. 红与黑(bfs dfs)

视频讲解

bfs—Flood fill算法–最短路

#include<bits/stdc++.h> 

#define x first
#define y second

using namespace std;
const int N = 25;
typedef pair<int, int> PII;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
int n, m;
char g[N][N];


int bfs(int sx, int sy)
{
    queue<PII> q;
    q.push({sx, sy});//起点 
    g[sx][sy] = '#';//被走过 
    int res = 0;//记录个数 

    while(q.size())
    {
        auto t=q.front();
        q.pop();
        res++;//每遍历一个点 

        for(int i=0;i<4;i++)
        {
            int x=t.x+dx[i],y=t.y+dy[i];
            if (x>=0 && x<n && y>=0 && y<m && g[x][y]=='.')//未出界且可走 
            {
            	g[x][y]='#';//标记 
            	q.push({x,y});//加入队列 
			}
            
        }
    }
    return res;
}
int main()
{
    while(cin>>m>>n, n || m)
    {
        int x,y;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++)
            {
            	cin>>g[i][j]; 
                if(g[i][j]=='@')
                {
                    x = i;
                    y = j;
                }
            }
        }
        cout<<bfs(x,y)<<endl;
    }
    return 0;
}

dfs—Flood fill算法—代码短

#include<bits/stdc++.h>
using namespace std;
int dx[]={-1,1,0,0},dy[]={0,0,-1,1};
const  int N=25;
int n,m;
char g[N][N];

int dfs(int x,int y)//参数---坐标 
{
	int res=1;//当前格子可以走 
	g[x][y]='#';
	
	for(int i=0;i<4;i++)
	{
		int a=x+dx[i],b=y+dy[i];
		if(a>=0 && a<n && b>=0 && b<m && g[a][b]=='.')
		{
			res+=dfs(a,b);
		}
	 } 
	return res;
}
int main()
{

	while(cin>>m>>n,m||n)//当在一行中读入的是两个零时，表示输入结束。 
	{
		int x,y;
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++)
			{
				cin>>g[i][j];
				if(g[i][j]=='@')
					x=i,y=j;
			}
		}
		cout<<dfs(x,y)<<endl;	
	 } 


	return 0;
}

AcWing2060. 奶牛选美—尽可能少的区域内涂色—Flood fill算法—枚举

AcWing2060. 奶牛选美
AcWing 2060. 奶牛选美详细证明

题目描述：在一个二维矩阵中，有两个点的集合，找到最短的距离(从一个集合到另一个集合中)距离的计算方式为(曼哈顿距离)
曼哈顿距离：两点间的曼哈顿距离 = | x1 - x2 | + | y1 - y2 |
输出最短距离

问题难点：
二维矩阵使用了字符类型存储
PII 上下左右的定义
dfs广度优先搜索的模板
floodfill算法的证明使用
Flood fill算法是从一个区域中提取若干个连通的点与其他相邻区域区分开（或分别染成不同颜色）的经典算法。

#include<iostream>
#include<bits/stdc++.h>
#include<vector> //数组 
using namespace std;
 
#define x first
#define y second

typedef pair<int,int> PII;
const int N = 55;//此处定义了数据范围 二维数组的大小 

int n,m;
char g[N][N]; 
vector<PII> points[2];//一共有两个点的集合 

int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};

void bfs(int x,int y,vector<PII>& ps)//洪水覆盖算法 
{
	g[x][y]='.';//将搜索过的点做标记 
	ps.push_back({x,y});//放入vector中去 
	
	for(int i=0;i<4;i++)
	{
		int a=x+dx[i];
		int b=y+dy[i];
		
		if(a>=0 && a<n && b>=0 && b<m && g[a][b] == 'X')//如果未超出界，且为x时 
		{
			bfs(a,b,ps);
		}
	}
}
int main()
{
	cin>>n>>m;
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			cin>>g[i][j];
		 
	
	for(int i=0 ,k=0;i<n;i++)
		for(int j=0;j<m;j++)
			if(g[i][j]=='X')//遇到x时，将位于同一集合中的所有x放入一个vector中去 
				bfs(i,j,points[k++]);//洪水覆盖算法----bfs版本 
	
	int res=1e8;//返回的距离长度，先初始化一个很大的距离
	
	for(auto& a:points[0])//枚举两个集合中的所有点 
		for(auto& b:points[1])
			res=min(res,abs(a.x-b.x)+abs(a.y-b.y)-1);//最优解---曼哈顿距离 

	
	cout<<res;
	return 0;
}

201512-3-csp-画图—洪水覆盖算法

AcWing 3224. 画图
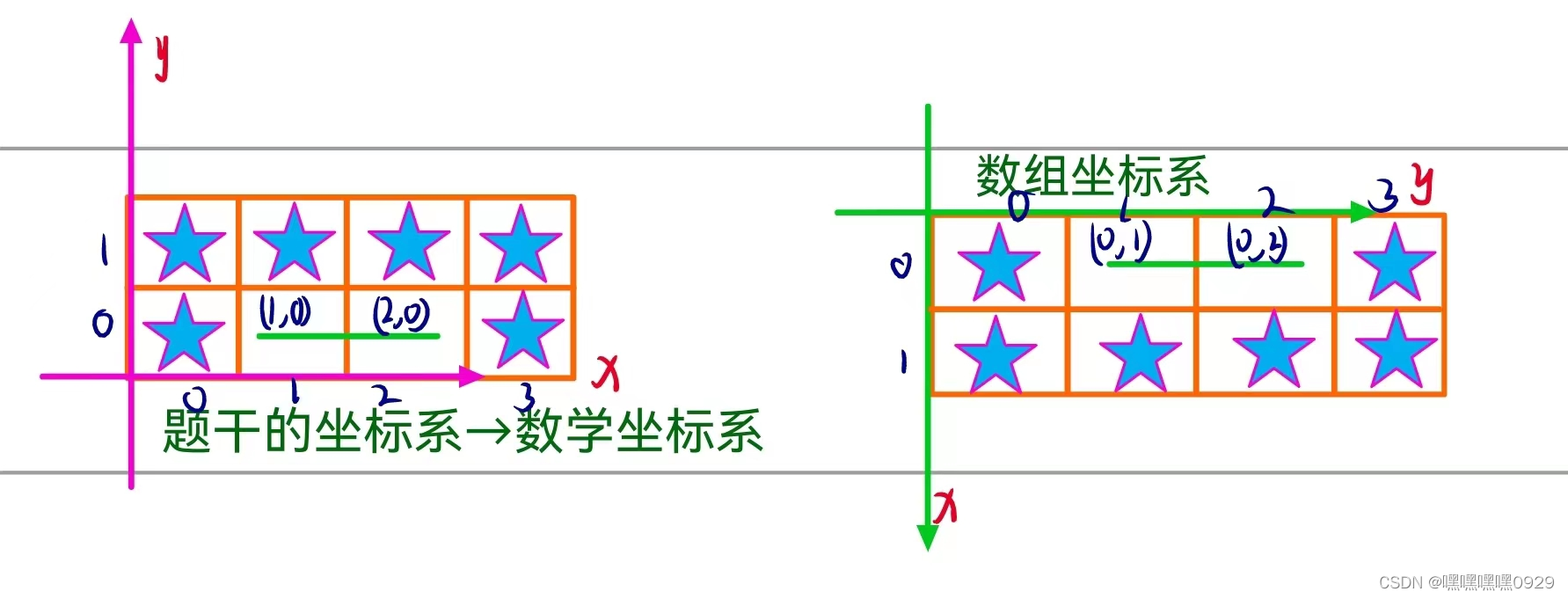
AcWing 3224. 画图(dfs：坐标反着读入，即可正常处理)

由数组坐标系(起点在左上角)---按数学坐标系输出(起点在左下角) 

DFS写法

#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;

char g[N][N];//地图 
bool st[N][N];//对某类型的标记 
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
int n,m;//n是高度(行)，m是宽度(列)


void paint(int x1,int y1,int x2,int y2)//划线函数 
{
	if(x1==x2)//属于同行 
	{
		for(int j=y1;j<=y2;j++)
		{
			if(g[x1][j]=='|'||g[x1][j]=='+')
				g[x1][j]='+';
			else
				g[x1][j]='-';
		 }
	}
	else if(y1==y2)//同列时
	{
		for(int i=x1;i<=x2;i++)
		{
			if(g[i][y1]=='-'||g[i][y1]=='+')
				g[i][y1]='+';
			else
				g[i][y1]='|';
		 } 
	 }
	return ; 
	
 } 
 
void dfs(int x,int y,char C)//洪水覆盖算法 
{
	st[x][y]=true;//对同类型的填充做标记 
	g[x][y]=C;
	
	for(int i=0;i<4;i++)
	{
		int a=x+dx[i];
		int b=y+dy[i];
		if(a<0 || a>=n || b<0 || b>=m || st[a][b])//不越界---未走过 
			continue;
		if(g[a][b]=='-' || g[a][b]=='|' || g[a][b]=='+')//不撞墙 
			continue;
		dfs(a,b,C);
	 } 
 } 
int main()
{
	int q;
	cin>>m>>n>>q; 
	for(int i=0;i<n;i++)//---正常的数组输入---在输入坐标是将(x,y)对调 
		for(int j=0;j<m;j++)
			g[i][j]='.';
	while(q--)
	{
		int op;//操作类型
		cin>>op;
		if(op==0)//划线
		{
			int x1,y1,x2,y2;
			cin>>x1>>y1>>x2>>y2;
			if(x1>x2) swap(x1,x2);//保证小的坐标在前---x/y至少有一项,两个点的坐标相同--同行/同列 
			if(y1>y2) swap(y1,y2);
			paint(y1,x1,y2,x2);//交换x---y 
		}
		else//填充 
		{
			int x,y;
			char C;
			cin>>x>>y>>C;
			memset(st,0,sizeof(st));//这里需要对状态数组重新初始化一下 
			dfs(y,x,C);//交换x---y 
			
		} 
	}
	for(int i=n-1;i>=0;i--)//由数组坐标系(起点在左上角)---按数学坐标系输出(起点在左下角) 
	{
		for(int j=0;j<m;j++)
		{
			cout<<g[i][j];
		}
		cout<<endl;
	 } 

}

BFS写法

#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;
typedef pair<int,int> PII;
char g[N][N];//地图 
bool st[N][N];//对某类型的标记 
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
int n,m;//n是高度(行)，m是宽度(列)


void paint(int x1,int y1,int x2,int y2)//划线函数 
{
	if(x1==x2)//属于同行 
	{
		for(int j=y1;j<=y2;j++)
		{
			if(g[x1][j]=='|'||g[x1][j]=='+')
				g[x1][j]='+';
			else
				g[x1][j]='-';
		 }
	}
	else if(y1==y2)//同列时
	{
		for(int i=x1;i<=x2;i++)
		{
			if(g[i][y1]=='-'||g[i][y1]=='+')
				g[i][y1]='+';
			else
				g[i][y1]='|';
		 } 
	 }
	return ; 
	
 } 
 
void bfs(int x,int y,char C)//洪水覆盖算法 
{
	queue<PII> q;
	q.push({x,y});
	st[x][y]=true;//对同类型的填充做标记 
	g[x][y]=C;
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		for(int i=0;i<4;i++)
		{
			int a=t.first+dx[i];
			int b=t.second+dy[i];
			if(a<0 || a>=n || b<0 || b>=m || st[a][b])//不越界---未走过 
				continue;
			if(g[a][b]=='-' || g[a][b]=='|' || g[a][b]=='+')//不撞墙 
				continue;
			q.push({a,b});
			st[a][b]=true;//对同类型的填充做标记 
			g[a][b]=C;
		
	 	} 
	}
	
 } 
int main()
{
	int q;
	cin>>m>>n>>q; 
	for(int i=0;i<n;i++)//---正常的数组输入---在输入坐标是将(x,y)对调 
		for(int j=0;j<m;j++)
			g[i][j]='.';
	while(q--)
	{
		int op;//操作类型
		cin>>op;
		if(op==0)//划线
		{
			int x1,y1,x2,y2;
			cin>>x1>>y1>>x2>>y2;
			if(x1>x2) swap(x1,x2);//保证小的坐标在前---x/y至少有一项,两个点的坐标相同--同行/同列 
			if(y1>y2) swap(y1,y2);
			paint(y1,x1,y2,x2);//交换x---y 
		}
		else//填充 
		{
			int x,y;
			char C;
			cin>>x>>y>>C;
			memset(st,0,sizeof(st));//这里需要对状态数组重新初始化一下 
			bfs(y,x,C);//交换x---y 
			
		} 
	}
	for(int i=n-1;i>=0;i--)//由数组坐标系(起点在左上角)---按数学坐标系输出(起点在左下角) 
	{
		for(int j=0;j<m;j++)
		{
			cout<<g[i][j];
		}
		cout<<endl;
	 } 

}

DFS—深度优先搜索

AcWing 842. 排列数字

AcWing 842. 排列数字
AcWing 842. 排列数字–深度优先遍历代码+注释

#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int st[N];//数字是否被用过
int n;
void dfs(int u)
{
    if(u>n)//数字填完了，输出
    {
        for(int i=1;i<=n;i++)//输出方案
            cout<<path[i]<<" ";
        cout<<endl;
    }

    for(int i=1;i<=n;i++)//空位上可以选择的数字为:1 ~ n
    {
        if(!st[i])//如果数字 i 没有被用过
        {
            path[u] = i;//放入空位
            st[i]=1;//数字被用，修改状态
            dfs(u+1);//填下一个位
            st[i]=0;//回溯，取出 i
            path[u]=0;
        }
    }
}

int main()
{
    cin >> n;
    dfs(1);
}

AcWing 843. n-皇后问题

AcWing 843. n-皇后问题

代码分析

    对角线 dg[u+i]

，反对角线udg[n−u+i]中的下标 u+i和 n−u+i

    表示的是截距

下面分析中的(x,y)
相当于上面的(u,i)

    反对角线 y=x+b

, 截距 b=y−x，因为我们要把 b 当做数组下标来用，显然 b 不能是负的，所以我们加上 +n
（实际上+n+4,+2n都行），来保证是结果是正的，即 y - x + n
而对角线 y=−x+b
, 截距是 b=y+x

    ，这里截距一定是正的，所以不需要加偏移量

核心目的：找一些合法的下标来表示dg
或udg是否被标记过，所以如果你愿意，你取 udg[n+n−u+i] 也可以，只要所有(u,i)对可以映射过去就行

AcWing 1432. 棋盘挑战—对角线—八皇后问题

AcWing 1432. 棋盘挑战

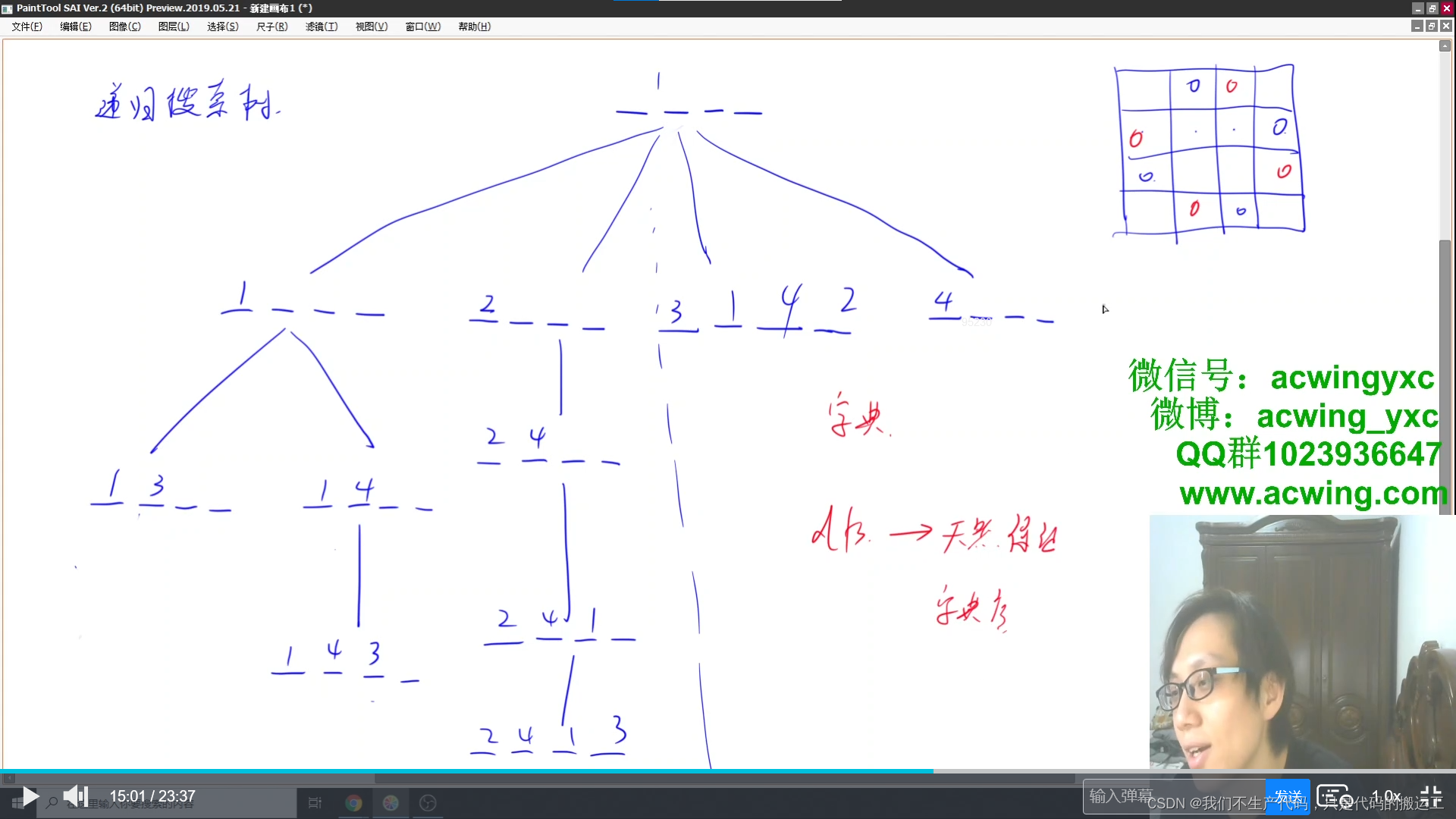
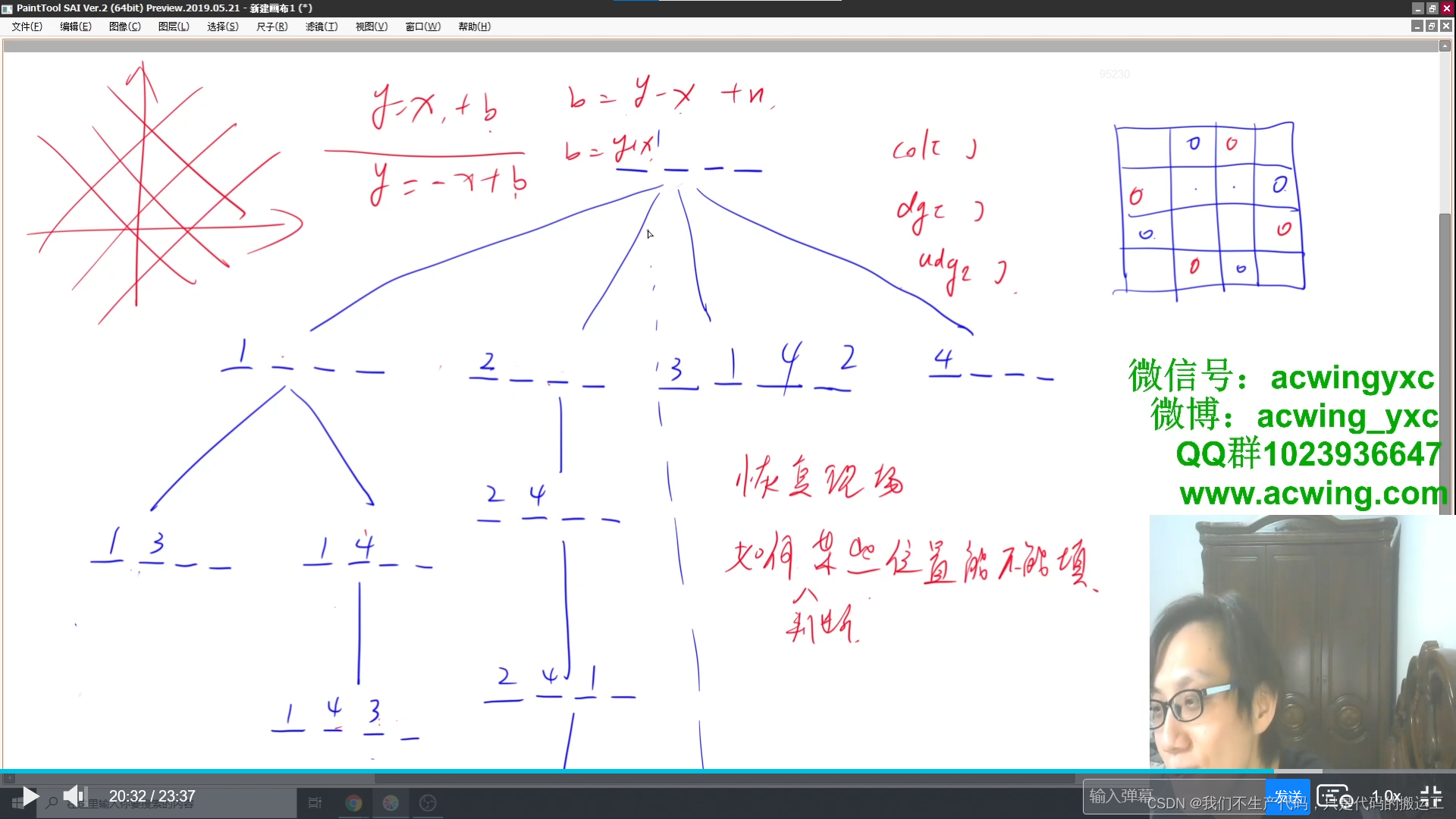
dfs--天然保证了按照字典序

#include<bits/stdc++.h>
using namespace std;
const int N=15;

int n;
bool col[N];//用于标志这列是否被存放了
bool dg[N*2];//正对角线上是否有了元素  true：有 ；false ：无 
//正对角线 ---存储b
//y=x+b  y=x+b  -> b=x-y; 
bool udg[N*2]; //反对角线上是否有了元素  true：有 ；false ：无
//副对角线 ---存储b
//y=-x+b y=-x+b  ->b=x+y; 
int path[N];//方案 
int ans;
void dfs(int x)
{
	if(x>n)//搜索到第n行---搜索到答案 
	{
		ans++;
		if(ans<=3)
		{
			for(int i=1;i<=n;i++)	cout<<path[i]<<" ";
			cout<<endl;
		}
		return ;
	}
	
	for(int y=1;y<=n;y++)//枚举一下放到第几列 
	{
		if(!col[y]&&!dg[x+y]&&!udg[x-y+n])//该列、正对角线、副对角线上都没有数 
		{
			path[x]=y;
			col[y]=dg[x+y]=udg[x-y+n]=true;//标记一下 
			
			dfs(x+1);//搜索下一层 
			
			col[y]=dg[x+y]=udg[x-y+n]=false;//恢复现场---清空 
			path[x]=0;
		}
	}
}
int main()
{
	cin>>n;
	dfs(1);
	cout<<ans<<endl;
	return 0;
 } 

201709-4-csp-通信网络—正反向两次dfs—图论

AcWing 3250. 通信网络
AcWing 3250. 通信网络—两次dfs

#include<bits/stdc++.h>
using namespace std;
const int N =1e3+10;//顶点 
const int M =1e4+10;//边
bool st1[N];
bool st2[N];
//邻接表---正向存储 
int idx1;
int e1[M];
int ne1[M];
int h1[N];

void add1(int a,int b)
{
	e1[idx1]=b;
	ne1[idx1]=h1[a];
	h1[a]=idx1++;
}
//邻接表---逆向存储
int idx2;
int e2[M];
int ne2[M];
int h2[N];


void add2(int a,int b)
{
	e2[idx2]=b;
	ne2[idx2]=h2[a];
	h2[a]=idx2++;
}


int n,m;

void dfs1(int u)
{
	st1[u]=true;//当前点已经被遍历过了
	for(int i=h1[u];i!=-1;i=ne1[i])
	{
		int j=e1[i];
		if(!st1[j])
			dfs1(j);	
	 } 	
}
void dfs2(int u)
{
	st2[u]=true;//当前点已经被遍历过了
	for(int i=h2[u];i!=-1;i=ne2[i])
	{
		int j=e2[i];
		if(!st2[j])
			dfs2(j);	
	 } 	
}

int main()
{
	cin>>n>>m;
	memset(h1,-1,sizeof(h1));//邻接表---顶点表---初始化
	memset(h2,-1,sizeof(h2));
	for(int i=0;i<m;i++)
	{
		int a,b;
		cin>>a>>b;
		add1(a,b),add2(b,a);//邻接表  与  逆邻接表
	}
	
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		memset(st1,0,sizeof(st1));
		memset(st2,0,sizeof(st2));
		dfs1(i);//正向搜索
		dfs2(i);//反向搜索
		int sum=0;
		for(int j=1;j<=n;j++)
		{
			if(st1[j]||st2[j])//只要有一个方向能搜索到就算可以
				sum++;
		}
		if(sum==n)
			ans++;
	}
	cout<<ans<<endl;
	return 0;
 } 

201312-5-csp-I’m stuck!—正反两个方向dfs

AcWing 3196. I’m stuck!

AcWing 3196. I’m stuck!：矩阵地图遍历 + 详细代码注释

#include<bits/stdc++.h>
using namespace std;
const int N=55;
char g[N][N];//存储地图 
bool st1[N][N];//true：从起点可以走到[i][j] 
bool st2[N][N];//true:从[i][j] 可以走到终点 
int R,C;
int ans;//返回符合答案的数目 
int dx[4]={-1,0,1,0};//上0-左1-下2-右3 
int dy[4]={0,1,0,-1};

bool check(int x,int y,int i)//判断是否能走 
{
	if(g[x][y]=='+'||g[x][y]=='S'||g[x][y]=='T')	return true;
	if(g[x][y]=='-'&& i%2!=0) return true;
	if(g[x][y]=='|'&& i%2==0)	return true;
	if(g[x][y]=='.'&& i==2) return true;
	return false;
}
void dfs1(int x,int y)//深度优先遍历，求出 S 能到的所有点
{
	st1[x][y]=true;
	for(int i=0;i<4;i++)
	{
		int a=x+dx[i];
		int b=y+dy[i];
		if(a<1||a>R || b<1||b>C ||g[a][b]=='#' ) 	continue;//走的位置不合法
		if(st1[a][b]) 	continue;//如果走过---跳过 
		if(check(x,y,i))//如果能走过去
			dfs1(a,b);
	 } 
}
void dfs2(int x,int y)//深度优先遍历，求出能走到 T 的所有点
{
	st2[x][y]=true;
	for(int i=0;i<4;i++)
	{
		int a=x+dx[i];
		int b=y+dy[i];
		if(a<1||a>R || b<1||b>C ||g[a][b]=='#' )	continue;//走的位置不合法
		if(st2[a][b])	continue;//如果走过---跳过
		if(check(a,b,i ^ 2))//如果能反向走过去---注意是那个点[a][b]---而不是[x][y]
			dfs2(a,b); 	
	}
 } 

int main()
{
	cin>>R>>C;
	for(int i=1;i<=R;i++)
		for(int j=1;j<=C;j++)
			cin>>g[i][j];
			
			
	int edx,edy;//记录下终点 
	for(int i=1;i<=R;i++)
		for(int j=1;j<=C;j++)
		{
			if(g[i][j]=='S')
				dfs1(i,j);//从起点开始dfs搜索可以到达的点 
			if(g[i][j]=='T')
			{
				edx=i,edy=j;
				dfs2(i,j);//从终点开始dfs搜索可以到达的点 
			}
		}
	if(!st1[edx][edy])//如果从起点到终点不可达直接输出
	{
		cout<<"I'm stuck!"<<endl;
		return 0; 
	} 
			
	for(int i=1;i<=R;i++)
		for(int j=1;j<=C;j++)
		{
			//cout<<st1[i][j]<<" "<<!st2[i][j]<<endl;
			if(st1[i][j] && !st2[i][j]) // S 能到 g[i][j], g[i][j] 不能到 T
				ans++;	 
		}
	cout<<ans<<endl;
	return 0;
}

201503-4-csp-网络延时—图论

AcWing 3215. 网络延时
详细讲解

#include<bits/stdc++.h>
using namespace std;
const int N=2e4+10;//这里交换机和计算机一起存储
const int M=N;
//邻接表存储图 
int idx;
int e[M];
int ne[M];
int h[N];

int n,m;
int ans;//最大深度+次大深度 
void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx++;
}


int dfs(int u)
{
	int d1=0,d2=0;//d1保存最大深度,d2保存次大深度
	
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int j=e[i];
		int d=dfs(j);//返回下一层的最大深度
		
		if(d>d1)
			d2=d1,d1=d;
		else if(d>d2)
			d2=d; 
	 }
	 ans=max(ans,d1+d2);
	 return d1+1; 
 } 



int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof(h));
	for(int i=2;i<=n;i++)
	{
		int p;
		cin>>p;
		add(p,i);//添加一条p->i的边---交换机->交换机 
	}
	for(int i=n+1;i<=n+m;i++)
	{
		int p;
		cin>>p;
		add(p,i);//添加一条p->i的边 ---交换机->计算机 
	 }
	 dfs(1);
	 cout<<ans<<endl; 
	return 0;
}

BFS—广度优先搜索

AcWing 844. 走迷宫—最短路(权重相同时)

AcWing 844. 走迷宫

#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;
typedef pair<int,int> PII;
#define x first
#define y second
int g[N][N]; 
int d[N][N];//存储从起点到达[i,j]位置的最短路径
int dx[4]={0,0,-1,1};
int dy[4]={-1,1,0,0}; 
int n,m;
int bfs()
{
	queue<PII> q;
	q.push({1,1});//将起点加入队列
	while(q.size()) 
	{
		auto t=q.front();//队首元素 
		q.pop();
		for(int i=0;i<4;i++)//将上下左右加入队列 
		{
			int X=t.x+dx[i];
			int Y=t.y+dy[i];
			if(X>=1 && X<=n && Y>=1 && Y<=m && g[X][Y]==0 && d[X][Y]==0)//未出界、不是墙、未走过、
			{
				d[X][Y]=d[t.x][t.y]+1;
				q.push({X,Y}); 
			 } 
		}
		
	}
	return d[n][m];//返回到达[n,m]的距离 
}
int main()
{

	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin>>g[i][j];
	cout<<bfs()<<endl; 
	return 0;
 } 

201604-4-csp-游戏—最短路—拆点(通过升维来对状态点进行细分)

AcWing 3230. 游戏

详细讲解

#include<bits/stdc++.h>
using namespace std;
const int N=110;
const int M=310;//最多花费300秒的时间就能走到终点 
bool g[N][N][M];//---g[x][y][t]---t时刻，(x,y)坐标是否能走---true：表示不能走
bool st[N][N][M];//---st[x][y][t]:表示(x,y)坐标 在t时刻是否走过---为了不重复走 

int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
int n,m,t;
struct Node{//结构体---方便队列存储信息 
	int x,y;
	int t;
};

int bfs()
{
	queue<Node> q;
	st[1][1][0]=true;//在0时刻---[1][1]位置已经走过 
	q.push({1,1,0});//将起点加入队列 
	
	while(q.size())
	{
		auto z=q.front();
		q.pop();
		
		for(int i=0;i<4;i++)
		{
			int x=z.x+dx[i];
			int y=z.y+dy[i];
			int t=z.t+1;
			
			if(x<1 || x>n || y<1 || y>m || g[x][y][t]) continue;//如果越界 或 [x][y]在t时刻不能走 
			if(st[x][y][t]) continue;//[x][y]在t时刻---已经经过该位置了 
				
			if(x==n && y==m)//到达终点 
				return t;
			st[x][y][t]=true;
			q.push({x,y,t});
		}
	}
	return -1;
}
int main()
{
	cin>>n>>m>>t;
	while(t--)
	{
		int r,c,a,b;
		cin>>r>>c>>a>>b;
		for(int i=a;i<=b;i++)
		{
			g[r][c][i]=true;//表示x,y这个格子在i时刻不能走
		}
	}
	int t=bfs();
	cout<<t<<endl;
	return 0;
}

201409-4-csp-最优配餐—最短路

AcWing 3205. 最优配餐
AcWing 3205. 最优配餐——多源BFS

#include<bits/stdc++.h>
using namespace std;
const int N =1e3+10;
const int INF =0x3f3f3f3f;
typedef long long LL;
typedef pair<int,int> PII;

bool st[N][N];//标记已经走过---和---原本就是障碍物 
int dist[N][N];//记录---多源起点到达该位置的最短距离
 
struct target{//存储买家的位置---订单数量 
	int x;
	int y;
	int c;
}Tg[N*N];

queue<PII> q;//bfs---队列---将坐标加入队列 
int n,m,k,d;
int dx[4]={-1,0,1,0};//上-右-下-左 
int dy[4]={0,1,0,-1};

void bfs()
{
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		
		for(int i=0;i<4;i++)
		{
			int a=t.first+dx[i];
			int b=t.second+dy[i];
			if(a>=1 && a<=n && b>=1 && b<= n && !st[a][b])
			{
				if(dist[a][b]>dist[t.first][t.second]+1)
				{
					dist[a][b]=dist[t.first][t.second]+1;//最短路径算法---边权相同---bfs 
					st[a][b]=true;
					q.push({a,b});
				}
			}
		}
	}
}
int main()
{
	cin>>n>>m>>k>>d;
	memset(dist,INF,sizeof(dist));//初始化一下所有位置---为不可达 
	while(m--)
	{
		int a,b;
		cin>>a>>b;
		dist[a][b]=0;//-----------将多元起点---标记为起点---初始距离 
		q.push({a,b});//将起点加入队列 
	}
	for(int i=0;i<k;i++)
		cin>>Tg[i].x>>Tg[i].y>>Tg[i].c;
	
	while(d--)
	{
		int a,b;
		cin>>a>>b;
		st[a][b]=true;//表示该位置不可达 
		}	

	bfs();
	LL ans=0;
	
	for(int i=0;i<k;i++)
		ans+=dist[Tg[i].x][Tg[i].y]*Tg[i].c;

	cout<<ans<<endl;
 
	return 0;
 } 

201403-4-csp-无线网络–拆点(通过升维来对状态点进行细分)

AcWing 3200. 无线网络

详细题解

#include<bits/stdc++.h>
using namespace std;
const int N=210;//非特殊点+特殊点 
const int M=N*N;//无向图 
const int INF=0x3f3f3f3f; 
typedef pair<int,int> PII;//存储每个点的位置信息 
PII p[N];
int dist[N][N]; // 最短距离，从1->i---dist[i][j]---i：到达点的编号，j:路线中经过了几个特殊点 
#define x first
#define y second
typedef long long LL;

int n,m,k,r;

//邻接表存储图
int idx;
int e[M];
int ne[M];
int h[N];

void add(int a,int b)//边权都为1 
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx++; 
 } 

bool check(PII a, PII b)
{
	LL dx=a.x-b.x;
	LL dy=a.y-b.y;
	return (dx*dx+dy*dy<=(LL)r*r);
 } 
int bfs()
{
	memset(dist,INF,sizeof(dist));
	dist[1][0]=0;//到达1号点，经过0个特殊点，路径距离=0 
	
	queue<PII> q;//----此时存储x:几号点，y经过几个特殊点 
	q.push({1,0});
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		
		for(int i=h[t.x];i!=-1;i=ne[i])
		{
			int j=e[i];//以i为边-----------t.x->j
			int y=t.y;
			if(j>n)//说明此时选择的终点---是特殊点 
				y++;
			if(y<=k)
			{
				if(dist[j][y]>dist[t.x][t.y]+1)
				{
					dist[j][y]=dist[t.x][t.y]+1;
					q.push({j,y});
				}
			 } 
		}
	 }
	 
	 int ans=1e8;
	 for(int i=0;i<=k;i++)
	 {
	 	ans=min(ans,dist[2][i]);
	  }
	return ans-1; 
}
int main()
{
	cin>>n>>m>>k>>r;
	memset(h,-1,sizeof(h)); 
	for(int i=1;i<=n;i++) cin>>p[i].x>>p[i].y;//原有路由器 
	for(int i=n+1;i<=n+m;i++)	cin>>p[i].x>>p[i].y;//新增路由器
	

	//初始化---点与点之间的距离 
	for(int i=1;i<=n+m;i++)
	{
		for(int j=i+1;j<=n+m;j++)
		{
			if(check(p[i],p[j]))
			{
				add(i,j),add(j,i);//无向图--每条边存储两次 
			}
		}
	}
	
	
	cout<<bfs()<<endl;
	
	return 0;
 } 

201509-4-csp-高速公路

AcWing 3220. 高速公路
暴力bfs 60分

#include <bits/stdc++.h>

using namespace std;

const int N = 1010, M = N * N;
#define x first
#define y second
typedef pair<int,int> PII;


int h[N], e[M], ne[M], idx;
int n, m;
bool g[N][N];

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

queue<PII> q;

void bfs()
{
    while(q.size())
    {
        auto t = q.front();
        q.pop();

        for(int j = h[t.y]; j != -1; j = ne[j])
        {
            if(g[t.x][e[j]])continue;
            q.push({t.x, e[j]});
            g[t.x][e[j]] = true;
        }
    }
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m;i  ++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        q.push({a, b});
    }

    bfs();
    int res = 0;
    for(int i = 1; i <= n; i ++)
    {
        for(int j = 1; j < i; j ++)
        {
            if(g[i][j] && g[j][i])res ++;

        }
    }

    cout << res << endl;
    return 0;
}

AcWing1101. 献给阿尔吉侬的花束—最短路

acwing1101. 献给阿尔吉侬的花束(bfs)

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
#include<queue>//广度优先搜索 
#define x first
#define y second
typedef pair<int,int> PII;
const int N=210;
int dx[]={-1,1,0,0},dy[]={0,0,-1,1};

int n,m;
char g[N][N];
int dist[N][N];


int bfs(PII start)
{
	queue<PII> Q;
	Q.push(start);
	memset(dist,-1,sizeof(dist)); //初始化数组为-1 
	dist[start.x][start.y]=0;//起点的距离为0 
	
	while(Q.size())
	{
		auto t =Q.front();
		Q.pop();
		for(int i=0;i<4;i++)
		{
		int x=t.x+dx[i],y=t.y+dy[i];//上下左右的坐标 
		if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]!='#'&&dist[x][y]==-1)//如果没有越界 
			{
				dist[x][y]=dist[t.x][t.y]+1;//更新距离 
				if(g[x][y]=='E')//到达终点 
					return dist[x][y];
				Q.push({x,y});//加入队列 
			}
			
		}
	}
return -1;//如果没有找到终点---当队列中没有点时----所有能走到的点都被标记了--(距离非0) 
}
int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		cin>>n>>m;
		PII start;
		for(int i=0;i<n;i++)
			for(int j=0;j<m;j++)
			{
				cin>>g[i][j]; 
				if(g[i][j]=='S')//如果为S，则为起点 
					start={i,j};
			}
		int res=bfs(start);
		if(res==-1)	cout<<"oop!"<<endl;
		else cout<<res<<endl;
	}
	return 0;
}

AcWing 845. 八数码—至少需要进行多少次交换

AcWing 845. 八数码
详细讲解

#include<bits/stdc++.h>
using namespace std;
int dx[4]={1,-1,0,0};
int dy[4]={0,0,-1,1};

int bfs(string strat)
{
	string ed="12345678x";//定义结束状态
	queue<string> q;
	unordered_map<string,int> m;
	
	q.push(strat);
	m[strat]=0;//起点距离
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		int dist=m[t];//如果是最终状态则返回距离
		if(t==ed)
			return dist; 
			
		int index=t.find('x');//查询x在字符串中的下标，然后转换为在矩阵中的坐标
		int x=index/3;
		int y=index%3;
		
		for(int i=0;i<4;i++)
		{
			int X=x+dx[i]; //求转移后x的坐标
			int Y=y+dy[i];
			if(X>=0 && X<3 && Y>=0 && Y<3) //当前坐标没有越界
			{
				swap(t[index],t[X*3+Y]);//转移x
				if(!m.count(t))//如果当前状态是第一次遍历，记录距离，入队
				{
					m[t]=dist+1;
					q.push(t);
				}
				swap(t[index],t[X*3+Y]);//还原状态，为下一种转换情况做准备
			}
		}
	 }
	 //无法转换到目标状态，返回-1
	 return -1; 
}
int main()
{
	string c,strat;//用字符串读入-----X 
	for(int i=1;i<=9;i++)
	{
		cin>>c;//字符串的输入是以空格截止 
		strat+=c;//字符串的拼接 
	}
	cout<<bfs(strat)<<endl; 
	return 0;
 } 

AcWing 3385. 玛雅人的密码

AcWing 3385. 玛雅人的密码

#include<bits/stdc++.h>
using namespace std;

int n;
int bfs(string start)
{
	queue<string> q;//存储字符串---广搜--队列
	unordered_map<string,int> dist;//存储到达字符串t的最近距离
	dist[start]=0;
	q.push(start);
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		
		if(t.find("2012")!=-1)//在字符串中查找目标状态
			return dist[t];
			
		for(int i=1;i<n;i++)//广度搜索
		{
			string r=t;
			swap(r[i],r[i-1]);
			if(!dist.count(r))//如果是第一次搜索到这个字符串---加入队列
			{
				dist[r]=dist[t]+1;
				q.push(r);
			}
		}
	}
	return -1;
}
int main()
{
	string start;
	cin>>n;
	cin>>start;
	cout<<bfs(start)<<endl;//广度优先搜索
 } 

拓扑排序

AcWing 848. 有向图的拓扑序列

AcWing 848. 有向图的拓扑序列
AcWing 848. 拓扑排序−−思路介绍+图解模拟+详细代码注释

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int M=1e5+10;
//邻接表存储有向图
int idx;
int e[M];
int ne[M];
int h[N];


int cnt[N];//记录每个点的入度
vector<int> ans;//保存拓扑排序---点的顺序 

int n,m;

void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int topsort()
{
	queue<int> q;

	for(int i=1;i<=n;i++)//将初始时 入度为0 的点加入队列 
		if(cnt[i]==0)   
		    q.push(i);
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		ans.push_back(t);//出队时，将其加入拓扑答案中
		
		for(int i=h[t];i!=-1;i=ne[i])
		{
			int j=e[i];// t->j的边
			cnt[j]--;//终点的入度--
			if(cnt[j]==0)
				q.push(j); 
		 } 
	 }
	  
	 if(ans.size()!=n)//ans中点的个数不等于n时，说明还有点不可以进行拓扑排序
	 	return -1;
	
}

int main()
{

	cin>>n>>m;
	memset(h,-1,sizeof(h));//经典错误---标准零分 
	for(int i=1;i<=m;i++)
	{
		int a,b;
		cin>>a>>b;
		add(a,b);
		cnt[b]++;//入度++ 	
	}
	
	auto t=topsort();

	if(t==-1)
		cout<<-1<<endl;
	else
		for(auto &x:ans)
			cout<<x<<" ";
	
	return 0;
}

最短路径之Dijkstra算法

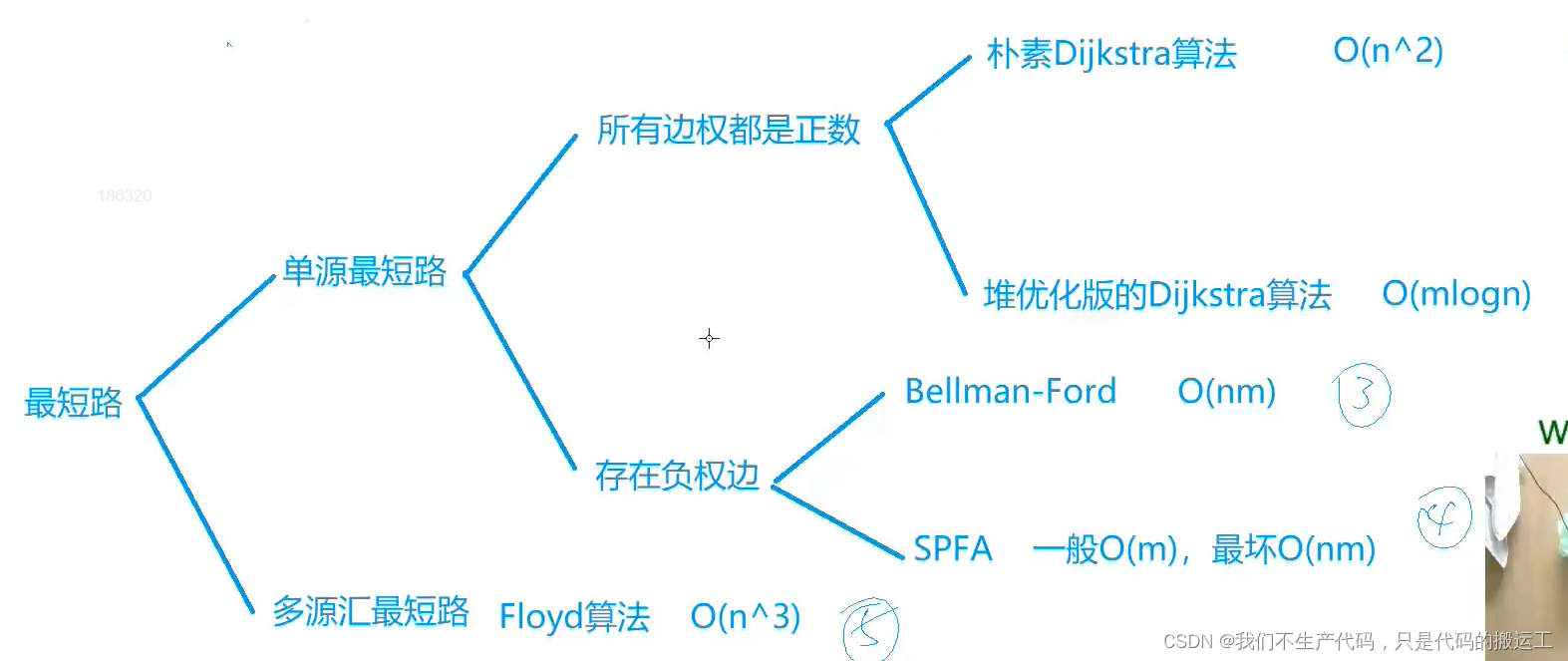
AcWing 849. Dijkstra求最短路 I—(重边√有环√—非负—有向/无向图√)—应用于稠密图

Dijkstra求最短路 I：图解 详细代码（图解）

#include<bits/stdc++.h>
using namespace std;
const int N =500+10;
const int INF=0x3f3f3f3f;
int g[N][N];
bool st[N];
int dist[N];
int n,m;
int dijkstra()
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0;//到1号点的距离为0 
	
	for(int i=1;i<n;i++)//再选择n-1个点 
	{
		int t=-1;
		for(int j=1;j<=n;j++)//选择最近的点
		{
			if(!st[j] && (t==-1||dist[j]<dist[t]))
				t=j; 
		 }
		 
		 st[t]=true;//状态数组---第一次选择的是起点---终点最终没有被选---终点是最后一个点
		 
		 for(int j=1;j<=n;j++)
		 {
		 	dist[j]=min(dist[j],dist[t]+g[t][j]);
		  } 
	 }
	 if(dist[n]!=INF)
	 	return dist[n];
	else
		return -1; 
}
int main()
{
	cin>>n>>m;
	memset(g,INF,sizeof(g));
	while(m--)
	{
		int x,y,c;
		cin>>x>>y>>c;
		g[x][y]=min(g[x][y],c);//盘重边 
	}
	cout<<dijkstra()<<endl; 
	return 0;
 } 

AcWing 850. Dijkstra求最短路 II------(重边√有环√—非负—有向/无向图√)—应用于稀疏图

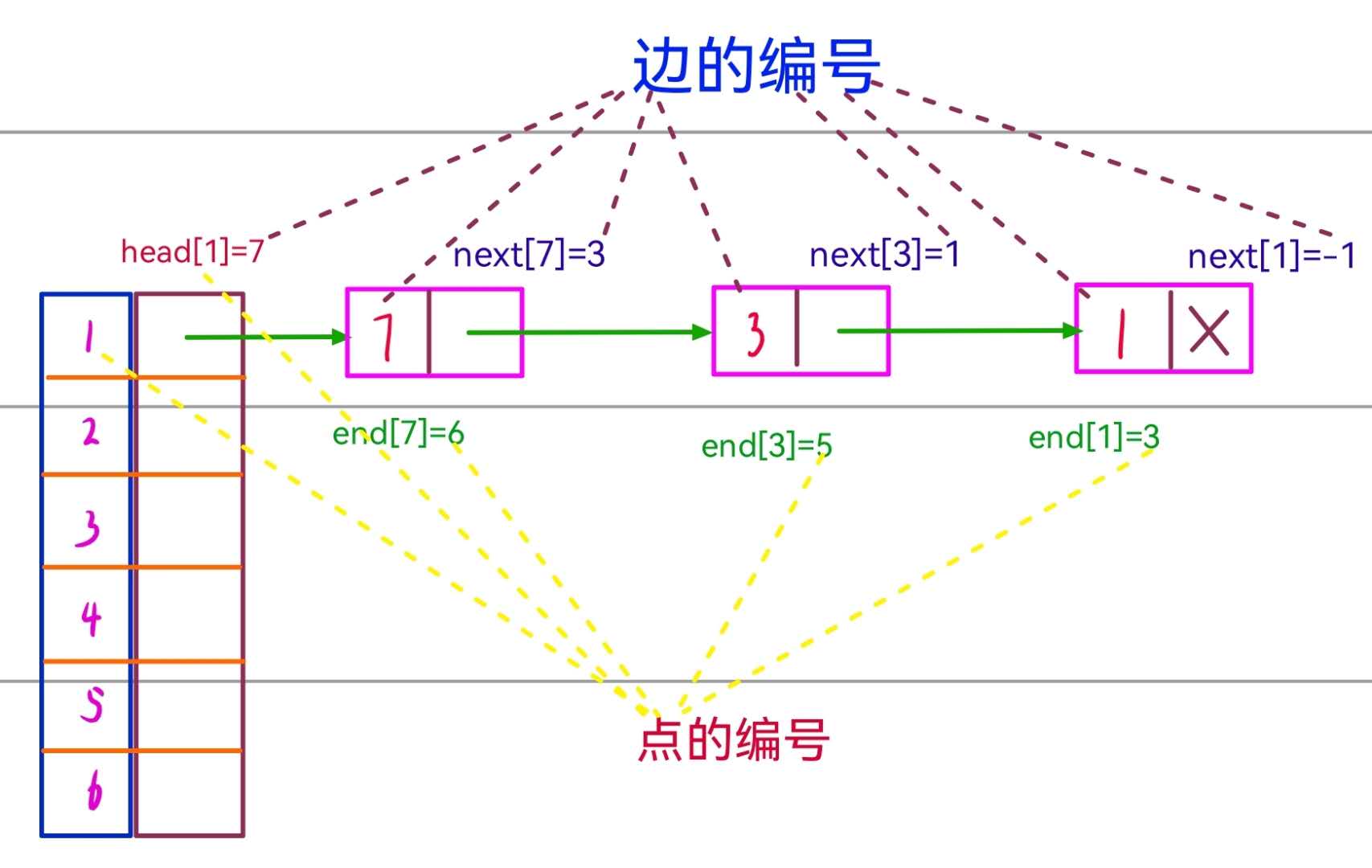
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;//边的最大数量 ---点的最大数量 
const int INF=0x3f3f3f3f;
typedef pair<int,int> PII;//存储每个点的信息---first：起点到i的距离，second:编号i
//点的信息
bool st[N]; 
int dist[N];

//邻接表存储方式 ---存储边
int idx;//边的编号
//编号为idx的边---的终点为e[i]
int e[N];//终点的编号---下标：边---存储：终点 
//上一条以a为起点的最大序号的边的序号是head[a] 
int ne[N];//起点的编号---下标：边---存储：起点(链接边表结点)
//编号为idx的边---的权值为w[i] 
int w[N];//存储第idx边的边权 ---下标：边---存储：边权

//---最后存进图的以x为起点的边的编号为h[x]
int head[N];//表头结点表---下标：点---存储：边



int n,m;
void add(int a,int b,int c)//输入的每条边都是由父节点 (a)子节点(b)和边权(c)组成的
{
	ne[idx]=head[a];//注意 ---(链接边表结点)上一条以a为起点的最大序号的边的序号是head[a] 
	e[idx]=b;
	w[idx]=c;
	head[a]=idx++;//现在以a为起点的最大序号的边的序号是idx了 
}
int dijkstra()
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	priority_queue<PII,vector<PII>,greater<PII>> heap;//定义小根堆
	heap.push({0,1});//把1号点放进去
	
	while(heap.size())
	{
		auto t=heap.top();
		heap.pop();//最小值出队---每次找到距离最小的点 
		
		int ver=t.second;
		int distance=t.first;
		
		
		if(st[ver])//如果更新过某点了---如果添加到S集合中了 
			continue;
		st[ver]=true;
		//用这个集合S所能到达的最小值更新---该点能到达的边的dist 
		for(int i=head[ver];i!=-1;i=ne[i])//i:边的编号 
		{
			int j=e[i];//这条边所能到达的终点---j：点的编号
			if(dist[j]>dist[ver]+w[i]) 
			{
				dist[j]=dist[ver]+w[i];//更新起点到任意一点的最短路
				heap.push({dist[j],j}); 
			}
		}
	 }
	 if(dist[n]!=INF)
	 	return dist[n];
	else
		return -1; 
}
int main()
{
	cin>>n>>m;
	memset(head,-1,sizeof(head));//把表头初始化为空节点 
	
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		add(a,b,c);//堆---不怕有重边
	 }
	 cout<<dijkstra()<<endl; 
	return 0;
 } 

bellman-ford—有边数限制的最短路问题

AcWing 853. 有边数限制的最短路

AcWing 853. 有边数限制的最短路
题干讲解

#include<bits/stdc++.h>
using namespace std;
const int N=500+10,M=1e4+10;
const int INF=0x3f3f3f3f;
//边结点数组 
struct{
	int a,b,w;
}edges[M];
int dist[N];
int backup[N];//辅助数组---防止串联 ---上一次迭代后 dist[] 数组的备份 
int n,m,k;

void bellman_ford()
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	//若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。
	for(int i=0;i<k;i++)//走k步 
	{
		memcpy(backup,dist,sizeof(dist));
		
		for(int j=0;j<m;j++)
		{
			int a=edges[j].a;
			int b=edges[j].b;
			int w=edges[j].w;
			dist[b]=min(dist[b],backup[a]+w);
		 } 
	}
}
int main()
{
	cin>>n>>m>>k;
	for(int i=0;i<m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		edges[i]={a,b,c};
	 }
	 
	 bellman_ford();
//INF是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，dist[n]大于某个与INF相同数量级的数即可	 
	 if(dist[n]>INF/2)
	 	cout<<"impossible"<<endl;
	else
		cout<<dist[n]<<endl;
	  
	return 0;
}

spfa

AcWing 851. spfa求最短路-带负权—有点小小万能的感觉?

AcWing 851. spfa求最短路

#include<bits/stdc++.h>
using namespace std;
const int N=1E5+10;
const int INF=0x3f3f3f3f;
bool st[N];//标记顶点是不是在队列中
int dist[N];//保存最短路径的值
//图的邻接表存储 
int idx;
int e[N];
int ne[N];
int w[N];
int h[N]; 

int n,m;
void add(int a,int b,int c)
{
	ne[idx]=h[a];
	e[idx]=b;
	w[idx]=c;
	h[a]=idx++;
 } 
int spfa()
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	queue<int> q;
	q.push(1);//将起点加入队列
	st[1]=true;
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		st[t]=false;//从队列中取出来之后该节点st被标记为false,代表之后该节点如果发生更新可再次入队
		
		for(int i=h[t];i!=-1;i=ne[i])//遍历邻接表中的顶点结点---后的相连边
		{
			int j=e[i];//获得和i相连的点
			if(dist[j]>dist[t]+w[i])//如果可以距离变得更短，则更新距离
			{
				dist[j]=dist[t]+w[i];//更新距离
				
		//当前已经加入队列的结点，无需再次加入队列，即便发生了更新也只用更新数值即可，重复添加降低效率
				if(!st[j])//如果没在队列中
				{
					q.push(j);//入队
					st[j]=true;//打标记
				 } 
			}
		}
		
	}
    return dist[n];
}
int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof(h));//注意---别忘了初始化---顶点表
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		add(a,b,c);//有向图  如果是无向图---+add(b,a,c) 
	}
	auto t=spfa();
	if(t==INF)
		cout<<"impossible"<<endl;
	else
		cout<<t<<endl;
	return 0; 
}

201609-4-csp-交通规划

AcWing 3235. 交通规划
详细讲解

#include<bits/stdc++.h>
using namespace std;

const int N=1e4+10;
const int M=2e5+10;//无向图存储---两条边
const int INF=0x3f3f3f3f;
bool st[N];
int dist[N];

//邻接表存储图
int e[M];//边 
int ne[M];
int w[M];
int h[N]; //点
int idx;
int n,m;

void add(int a,int b,int c)//向有向图中添加边---邻接表 
{
	e[idx]=b;
	w[idx]=c;
	ne[idx]=h[a];//注意---这里又写错了 
	h[a]=idx++;
 } 
 
void spfa()//-----spfa的代码还是不熟练
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0; 
	queue<int> q;//注意---队列里存储的是--点的编号 
	q.push(1);
	st[1]=true;//表示在队列中 
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		st[t]=false;
	
		
		for(int i=h[t];i!=-1;i=ne[i])
		{
			int j=e[i];//  t->j这条边
			if(dist[j]>dist[t]+w[i])
			{
				dist[j]=dist[t]+w[i];
				if(!st[j])//注意---这里需要判断一下是否需要加入队列 
				{
					st[j]=true;
					q.push(j);//更新过谁---我就拿这个更新过的点来更新别人
				}
			 } 
		 } 
		
	}
}
int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof(h));
	
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		add(a,b,c);//无向图 
		add(b,a,c);
	}

	spfa();
	
	 //求每个点满足条件的邻边(每个点的满足条件的边中权值最小的边就是我们要找的边)
	int ans=0;
	for(int a=2;a<=n;a++)//从其余的n-1个点中选
	{
		int minw=INF;//用minw表示权值最小的边
		for(int i=h[a];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(dist[a]==dist[j]+w[i])
			{
				minw=min(minw,w[i]);
			}
		}
		ans+=minw;//将每个点满足条件的权值最小边累加起来 
	 } 
	cout<<ans<<endl;
	 
	return 0;
 } 

201903-5-csp-317号子任务

AcWing 3276. 317号子任务

详细讲解

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
const int M=2e4+10;//无向图---每条边存储两次
const int INF=0x3f3f3f3f;
int idx;
int e[M];
int ne[M];
int w[M];
int h[N];

int dist[N];
int st[N];

int ds[N][1010];
int cnt;//记录到第几个行星发动机据点
int type[N];//记录据点的类型
int n,m,k;

void add(int a,int b,int c)
{
	e[idx]=b;
	w[idx]=c;
	ne[idx]=h[a];
	h[a]=idx++;
}
void spfa(int start)//每次从起点strat开始求---单源最短路径
{
	memset(dist,INF,sizeof(dist));//每次单元最短路径都有自己的dist st数组
	memset(st,0,sizeof(st));
	
	dist[start]=0;
	queue<int> q;
	q.push(start);
	st[start]=true;
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		
		st[t]=false;
		
		for(int i=h[t];i!=-1;i=ne[i])
		{
			int j=e[i];//  t->j;
			if(dist[j]>dist[t]+w[i])
			{
				dist[j]=dist[t]+w[i];
				if(!st[j])
				{
					st[j]=true;
					q.push(j);
				}
			 } 
		}
	}
	
	for(int i=1;i<=n;i++)//将第cnt行星发动机据点---到---所有据点的最短路径存储下来
		ds[i][cnt]=dist[i];

}
int main()
{
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
		cin>>type[i];
	memset(h,-1,sizeof(h));//因为图还是哪一个图---仅存储一次，从不同的点求单源最短路径
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		add(a,b,c),add(b,a,c);//无向图---将有向边存储两次---小心数组越界
	 }
	 
	 for(int i=1;i<=n;i++)
	 {
	 	if(type[i])
	 	{
	 		spfa(i);//从每个行星发动机开始进行spfa算法
	 		cnt++;
		 }
	  }
	  
	  
	  
	for(int i=1;i<=n;i++)//枚举所有的据点---找到---不是行星发动机的据点
	{
		int ans=0;
		sort(ds[i],ds[i]+cnt);//将第i个据点到所有行星发动机据点的距离排序
		
		for(int j=0;j<k && j<cnt;j++)
		{
			if(ds[i][j]!=INF)
				ans+=ds[i][j];
			else    //当排序后有一个行星发动机不可达，剩下的所有行星发动机都不可达
				break;
		 } 
		 cout<<ans<<endl;
	 } 
	
	return 0;
	
	 
 } 

AcWing 3255. 行车路线

AcWing 3255. 行车路线

AcWing 3255. 行车路线讲解

#include<bits/stdc++.h>
using namespace std;
const int N=510;//点数
const int M=2e5+10;//边数---注意无向边*2 
const int R=1e3+10;//纬度数---到达第i个点的路径上与i点直接相连的小道长度 

const int INF=0x3f3f3f3f;//为了方便输出最小花费 
typedef pair<int,int> PII;//[点的编号]---[到达i点的小道的长度] 
#define x first
#define y second
int dist[N][R];//dist[i][j]:      (从起点到达i点)且(与i点直接相连的小道长度为j)的最短距离 
bool st[N][R]; //spfa的状态数组
//邻接表存储图 
int idx;
int e[M];
int ne[M];
int h[N];
int w[M];
int type[M];

void add(int t,int a,int b,int c)
{
	type[idx]=t;
	w[idx]=c;
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx++;
}

void spfa()// 求1号点到n号点的最短路距离
{
	memset(dist,INF,sizeof(dist));
	memset(st,0,sizeof(st));
	
	queue<PII> q;
	q.push({1,0});
	st[1][0]=true;
	dist[1][0]=0;
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		st[t.x][t.y]=false;
		
		for(int i=h[t.x];i!=-1;i=ne[i])
		{
			int j=e[i];//t.x---->j的边(编号为i)
			if(type[i])//type为1时---小道 
			{
				if(dist[j][t.y+w[i]]>dist[t.x][t.y]-pow(t.y,2)+pow(t.y+w[i],2) && t.y+w[i]<=R)
				{
					dist[j][t.y+w[i]]=dist[t.x][t.y]-pow(t.y,2)+pow(t.y+w[i],2);
					if(!st[j][t.y+w[i]] && dist[j][t.y+w[i]]<=1e6)
					{
						st[j][t.y+w[i]]=true;
						q.push({j,t.y+w[i]});
					}
				}
			 }
			else//因为是大道---所以用dist[x][0] 
			{
			 	if(dist[j][0]>dist[t.x][t.y]+w[i])
				 {
				 	dist[j][0]=dist[t.x][t.y]+w[i];
				 	if(!st[j][0] && dist[j][0]<=1e6)
				 	{
				 		st[j][0]=true;
				 		q.push({j,0});
				 		
					 }
				  } 
			 } 
		}
	}
}
int main()
{
	int n,m;
	cin>>n>>m;
	memset(h,-1,sizeof(h)); 
	for(int i=1;i<=m;i++)
	{
		int t,a,b,c;
		cin>>t>>a>>b>>c;
		add(t,a,b,c);
		add(t,b,a,c);//无向图---两条边 
	}
	spfa();
	
	int ans=INF;
	for(int i=0;i<R;i++)
		ans=min(ans,dist[n][i]);
	cout<<ans<<endl;
	return 0;
}

AcWing 852. spfa判断负环

AcWing 852. spfa判断负环

#include<bits/stdc++.h>
using namespace std;
const int N=1E5+10;
const int INF=0x3f3f3f3f;
bool st[N];
int dist[N];
int cnt[N];//记录最短路径的长度 

int idx;
int e[N];
int ne[N];
int w[N];
int h[N]; 

int n,m;
void add(int a,int b,int c)
{
	ne[idx]=h[a];
	e[idx]=b;
	w[idx]=c;
	h[a]=idx++;
 } 
int spfa()
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	queue<int> q;
	for(int i=1;i<=n;i++)//---不同之处---将所有点都加入队列
    {
        st[i]=true;
        q.push(i);
    }
	
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		st[t]=false;
		for(int i=h[t];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(dist[j]>dist[t]+w[i])
			{
				dist[j]=dist[t]+w[i];
				cnt[j]=cnt[t]+1;//最短路径长度的变化
				
				if(cnt[j]>=n)
					return true;//有负环---负权回路 
				
	
				if(!st[j])
				{
					q.push(j);
					st[j]=true;
				 } 
			}
		}
		
	}
    return false;
}
int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof(h));//注意---别忘了初始化---顶点表
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		add(a,b,c);//有向图  如果是无向图---+add(b,a,c) 
	}
	 if (spfa()) puts("Yes");
    else puts("No");

	return 0; 
}

Floyd

AcWing 854. Floyd求最短路

最短路径算法之floyd算法
AcWing 854. Floyd求最短路

#include<bits/stdc++.h>

using namespace std;

const int N = 210, INF = 1e9;

int n, m, Q;
int d[N][N];

void floyd()
{
    for (int k = 1; k <= n; k ++ )//从i到j---从i到k+从k到j 
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main()
{
    scanf("%d%d%d", &n, &m, &Q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0;
            else d[i][j] = INF;

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        d[a][b] = min(d[a][b], c);
    }

    floyd();

    while (Q -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);

        int t = d[a][b];
        if (t > INF / 2) puts("impossible");
        else printf("%d\n", t);
    }

    return 0;
}

最小生成树

AcWing 858. Prim算法求最小生成树

AcWing 858. Prim算法求最小生成树

#include<bits/stdc++.h>
using namespace std;
const int N =500+10;
const int INF=0x3f3f3f3f;
int g[N][N];
bool st[N];
int dist[N];
int n,m;
int prim()
{
	memset(dist,INF,sizeof(dist));
	dist[1]=0;
	int res=0; //不同之处
	
	for(int i=0;i<n;i++)//选择n个点 ---与dijkstra(n-1次)不同，prim需要迭代n次
	{
		int t=-1;
		for(int j=1;j<=n;j++)
		{
			if(!st[j] && (t==-1||dist[j]<dist[t]))
				t=j; 
		 }
		 
		 
		 if (dist[t]==INF) return INF;//这里和dijkstra不同 
		 
		 st[t]=true;
		 
		 res+=dist[t];//这里和dijkstra不同 
		 
		 for(int j=1;j<=n;j++)
		 {
		 	dist[j]=min(dist[j],g[t][j]);//这里和dijkstra不同---更新方式不同 
		  } 
	 }
	 return res; 
}
int main()
{
	cin>>n>>m;
	memset(g,INF,sizeof(g));
	while(m--)
	{
		int x,y,c;
		cin>>x>>y>>c;
		g[x][y]=g[y][x]=min(g[x][y],c);//无向图 
	}
	 int res = prim();
    if (res == INF) 
        puts("impossible");
    else 
        printf("%d\n", res);
	return 0;
 } 

AcWing 859. Kruskal算法求最小生成树

AcWing 859. Kruskal算法求最小生成树

最小生成树之克鲁斯卡尔算法(Kruskal)

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;

    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if (p[x] != x) 
			p[x] = find(p[x]);
	return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0;//最小生成树的边权之和 
	int cnt = 0;//统计最小生成树的边的个数 
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;//如果最后边数不够时 
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

201412-4-csp-最优灌溉—非常裸的最小生成树问题

AcWing 3210. 最优灌溉

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
const int M=1e5+10;

struct Edge{//---存储边的信息
	int a;
	int b;
	int c;
	bool operator<(const Edge& t)const
	{
		return c<t.c;
	}
}edges[M];
int p[N];//并查集数组
int find(int x)
{
	if(x!=p[x])
		p[x]=find(p[x]);
	return p[x];
 } 
int n,m;
int kruskral()
{
	for(int i=1;i<=n;i++)//初始化
		p[i]=i;
	sort(edges,edges+m);//对边按权重排序---选择小边
	int ans=0;
	int cnt=0;//统计边的数量
	for(int i=0;i<m;i++)
	{
		int a=edges[i].a;
		int b=edges[i].b;
		int c=edges[i].c;
		
		if(find(a)!=find(b))
		{
			ans+=c;
			p[find(a)]=find(b);
			cnt++;
		}
	}
	if(cnt<n-1)//如果边数不够时---报错
	    return -1;
	return ans;
	
}
int main()
{
	cin>>n>>m;
	for(int i=0;i<m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		edges[i]={a,b,c};
	}
	auto t=kruskral();
	cout<<t<<endl;
	return 0;
}

201703-4-csp-地铁修建

AcWing 3245. 地铁修建

通过kruskal进行求解，加入的额外的更小权值的边并不影响结果
所以从小到大进行加入边权知道1与n节点在同一个连通块中，可达，此时的边权即是结果

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int M=2e5+10;

struct Edge{
	int a,b,c;
	bool operator<(const Edge& t) const
	{
		return c<t.c;
	}
}edges[M];
int p[N];
int find(int x)
{
	if(x!=p[x])//这里最好不要加if else
		p[x]=find(p[x]);
	return p[x];//一直找到根节点 
}
int n,m;
int maxw;
void kruskral()
{
	for(int i=1;i<=n;i++) p[i]=i;
	
	sort(edges,edges+m);


	for(int i=0;i<m;i++)
	{
		int a=edges[i].a;
		int b=edges[i].b;
		int c=edges[i].c;
		if(find(a)!=find(b))
		{
			p[find(a)]=find(b);
			if(find(1)==find(n))
			{
				maxw=c;//保存最大的边权 
				return ;
			}
			
		}
	 }

}
int main()
{
	cin>>n>>m;
	for(int i=0;i<m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		edges[i]={a,b,c};
	}
	
	kruskral();
	cout<<maxw<<endl;
	return 0;
}

201812-4-csp-数据中心

Wing 3270. 数据中心
Wing 3270. 数据中心（最小生成树之最大边权最小）

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int M=2e5+10;

struct Edge{
	int a,b,c;
	bool operator<(const Edge& t) const
	{
		return c<t.c;
	}
}edges[M];
int p[N];
int find(int x)
{
	if(x!=p[x])//这里最好不要加if else
		p[x]=find(p[x]);
	return p[x];//一直找到根节点 
}
int n,m;
int maxw;
void kruskral()
{
	for(int i=1;i<=n;i++) p[i]=i;
	
	sort(edges,edges+m);


	for(int i=0;i<m;i++)
	{
		int a=edges[i].a;
		int b=edges[i].b;
		int c=edges[i].c;
		if(find(a)!=find(b))
		{
			p[find(a)]=find(b);
				maxw=c;//保存最大的边权
		}
	 }
	return ;

}
int main()
{
	cin>>n;
	cin>>m;
	int root;
	cin>>root;
	for(int i=0;i<m;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		edges[i]={a,b,c};
	}
	
	kruskral();
	cout<<maxw<<endl;
	return 0;
}

欧拉路径

201512-4-csp-送货

AcWing 3225. 送货

直接将邻接表放到set里做,自动判重、排序,保证输出的是最小字典序
判断欧拉路径的初始条件后直接dfs就行了

#include<bits/stdc++.h> 
using namespace std;
const int N = 10010, M = 100010;

int n, m;
set<int> g[N];//邻接表存储---集合实现 
int p[N];//并查集数组 
int ans[M], top;//保存了反向答案 

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void dfs(int u)
{
    while (g[u].size())//当还有临边时
    {
        int t = *g[u].begin();//边的终点
        g[u].erase(t), g[t].erase(u);//删除这条边
        dfs(t);
    }
    ans[ ++ top] = u;//记录答案
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) p[i] = i;
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        g[a].insert(b), g[b].insert(a);
        p[find(a)] = find(b);
    }

    int s = 0;//欧拉路径---奇数条边点个数=0/2(其中一个是起点，一个是终点) 
    for (int i = 1; i <= n; i ++ )
        if (find(i) != find(1))
        {
            puts("-1");
            return 0;
        }
        else if (g[i].size() % 2) s ++ ;

    if (s != 0 && s != 2 || s == 2 && g[1].size() % 2 == 0)
    {
        puts("-1");
        return 0;
    }
    dfs(1);

    for (int i = top; i; i -- )
        printf("%d ", ans[i]);

    return 0;
}

染色法判定二分图

匈牙利算法