题目

标题和出处

标题：平衡二叉树

出处：110. 平衡二叉树

难度

4 级

题目描述

要求

给定一个二叉树，判断它是否是高度平衡的二叉树。

这道题中，一个高度平衡二叉树定义为：二叉树中每个结点的左右两个子树的高度差的绝对值不超过 $\text{1}$。

示例

示例 1：

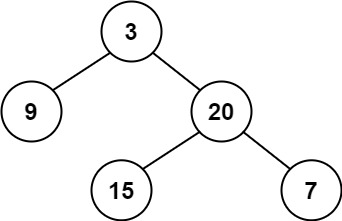
输入：$\text{root = [3,9,20,null,null,15,7]}$
输出：$\text{true}$

示例 2：

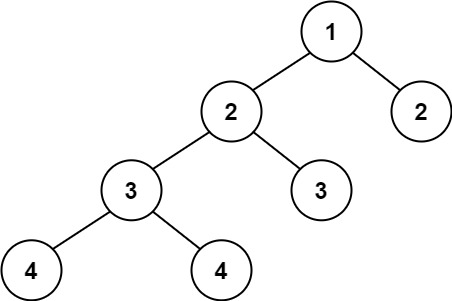
输入：$\text{root = [1,2,2,3,3,null,null,4,4]}$
输出：$\text{false}$

示例 3：

输入：$\text{root = []}$
输出：$\text{true}$

数据范围

• 树中结点数目在范围 $\text{[0, 5000]}$ 内
• ${\text{-10}}^{\text{6}}\le \text{Node.val}\le {\text{10}}^{\text{6}}$

解法一

思路和算法

只要得到二叉树中的每个子树的高度，即可判断二叉树是否高度平衡。

规定空二叉树的高度是 $0$，当二叉树非空时，二叉树的高度是从根结点到最深叶结点的路径上的结点数。

在得到二叉树中的每个子树的高度之后，即可判断二叉树中的每个子树是否高度平衡，并判断原始二叉树是否高度平衡。一个二叉树高度平衡，等价于其左子树和右子树的高度差的绝对值不超过 $1$，且左子树和右子树都高度平衡。

可以使用深度优先搜索实现，从根结点开始遍历每个结点，得到每个子树的高度并判断每个子树是否高度平衡。计算每个子树的高度和判断每个子树是否高度平衡的过程都是递归的过程。

计算每个子树的高度的递归终止条件是当前子树为空，此时高度是 $0$。对于其余情况，首先计算当前结点的左子树和右子树的高度，然后得到以当前结点为根结点的子树的高度是左子树和右子树的高度中的最大值加 $1$。

判断每个子树是否高度平衡的的递归终止条件是当前子树为空，此时高度平衡。对于其余情况，根据左子树和右子树的高度差的绝对值是否不超过 $1$ 以及左子树和右子树是否高度平衡判断当前子树是否高度平衡。

代码

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        return Math.abs(getHeight(root.left) - getHeight(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int getHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }
        return Math.max(getHeight(node.left), getHeight(node.right)) + 1;
    }
}

复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 是二叉树的结点数。每个结点都被访问一次，计算每个子树高度的时间取决于二叉树的高度，最坏情况下计算每个子树高度的时间是 $O(n)$，此时总时间复杂度是 $O(n^2)$。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。空间复杂度主要是递归调用的栈空间，取决于二叉树的高度，最坏情况下二叉树的高度是 $O(n)$。

解法二

思路和算法

解法一的时间复杂度较高，因为存在重复计算每个子树的高度的情况。为了降低时间复杂度，应避免重复计算，确保每个子树的高度只计算一次。

由于这道题要求判断二叉树是否高度平衡，不需要知道二叉树的具体高度，因此可以在计算每个子树的高度时同步判断子树是否高度平衡。由于每个子树的高度一定是非负数，因此可以将高度记为 $-1$ 表示一个子树高度不平衡。

计算每个子树的高度仍使用递归的方法。递归终止条件是当前子树为空，此时高度是 $0$，高度平衡。对于其余情况，首先计算当前结点的左子树和右子树的高度以及是否高度平衡，然后计算以当前结点为根结点的子树的高度，具体做法如下。

1. 如果左子树和右子树的高度中存在 $-1$，则相应的子树高度不平衡，以当前结点为根结点的子树也高度不平衡，返回 $-1$。

2. 如果左子树和右子树都高度平衡，且左子树和右子树高度差的绝对值超过 $1$，则以当前结点为根结点的子树高度不平衡，返回 $-1$。

3. 如果左子树和右子树都高度平衡，且左子树和右子树高度差的绝对值不超过 $1$，则以当前结点为根结点的子树高度平衡，计算当前高度是左子树和右子树的高度中的最大值加 $1$，返回当前高度。

由于只有高度平衡的二叉树的高度才是非负数，因此可以根据原始二叉树的高度是否大于等于 $0$ 判断原始二叉树是否高度平衡。

由于当一个子树高度不平衡时将 $-1$ 作为其高度返回，不会再次递归地计算高度，因此上述做法可以确保每个子树的高度只计算一次，将时间复杂度降低到 $O(n)$。

代码

class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) >= 0;
    }

    public int getHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int heightLeft = getHeight(node.left);
        if (heightLeft < 0) {
            return -1;
        }
        int heightRight = getHeight(node.right);
        if (heightRight < 0) {
            return -1;
        }
        if (Math.abs(heightLeft - heightRight) > 1) {
            return -1;
        }
        return Math.max(heightLeft, heightRight) + 1;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。每个结点最多被访问一次。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。空间复杂度主要是递归调用的栈空间，取决于二叉树的高度，最坏情况下二叉树的高度是 $O(n)$。